摘要:專業的大型磁盤存儲系統均發展為包含多塊磁盤的大型陣列系統。隨著系統中的磁盤數目的不斷增加，由磁盤失效引起的數據丟失的可能性越來越大。對于由存儲系統中部分磁盤失效所引起的數據丟失的問題，目前業界公認的比較好的解決方案是使用冗余容錯編碼技術來實現磁盤的容錯。在工程實踐中，目前廣泛應用的編碼方法大多局限于雙容錯陣列碼。隨著系統規模的進一步加大，3容錯甚至更多容錯的編碼方法已引起研究者的重視。今后的5至10年間，對于3容錯或多容錯的編碼方法的研究將會成為新的熱點。

1 存儲容錯編碼評價指標

近20年來，隨著計算機技術的迅猛發展，大規模存儲系統的發展也十分迅速。當前，普通PC機的存儲器的容量已經達到了太比特級別，這較之20年前的20 MB存儲容量提高了10 000倍。

除了傳統的磁盤驅動器之外，新型的固態存儲(SSD)存儲器也已經走向市場。盡管單個存儲器的容量發展迅速，但是卻仍然趕不上人們對存儲容量需求的增長速度。

隨著大型計算機系統由“以計算為中心”向著“以信息處理為中心”的轉變，以及信息量的爆炸式增長，人們對海量存儲系統的需求日益提高。海量存儲系統本質上是將很多的單個存儲器件(下面均以磁盤為例)，通過系統的接口，連接整合為一個虛擬的容量巨大的單一存儲器，即磁盤陣列。

隨著陣列中磁盤數目的增多，系統的可靠性也隨之下降。工業界一般使用平均數據丟失時間(MTTDL)來衡量陣列的可靠性。

設單個磁盤的平均失效時間為MTTFdisk，則對于包含n塊磁盤的無冗余陣列來說，其MTTDL可簡單估計為：MTTDL=MTTFdisk/n。可見，當n較大時，整個系統的可靠性將成比例下降。這對于較大規模的系統來說是不可接受的。利用冗余數據編碼來提高系統可靠性是公認的解決這一問題的較好方法。通過巧妙地將m塊標準大小的磁盤上的數據，增加部分冗余校驗信息，編碼后存放于n塊磁盤上，使得系統滿足：對于任意k塊磁盤失效，都可以通過其他n-k塊未失效盤中的數據解碼恢復，則稱整個系統是k容錯的，或者稱k為系統的容錯數。

分析表明[1]，對于k容錯的系統來說，可以近似估計為：

因而，在大規模系統中，容錯數可以說是另一種對系統可靠性的描述方式。市場中一般磁盤的MTTFdisk為105左右，系統修復時間MTTR一般為10左右。根據(1)式可以看出，當系統磁盤數為103～104時，一般2容錯或是3容錯編碼就基本上可以滿足存儲系統的容錯要求。

系統用于增加容錯能力而添加的冗余越多，系統的額外造價也將越高。因而在具有相同容錯數的前提下，人們往往追求更小的冗余度，即(n-m)/n的值，其中n為系統磁盤數、m為存儲用戶數據的磁盤數。根據編碼理論的Singleton界，k容錯系統的最小冗余度為：k/n。達到這一最小值的編碼方法稱做MDS碼。目前多數存儲編碼研究都集中于構造不同參數下的MDS碼。

除了上述指標，任何計算機系統的速度與效率永遠是需要考量的重要指標。這里我們不討論如何有效地并行處理多磁盤中的數據讀取(那是另外一個較大的課題)，而著重研究由于冗余編碼帶來的額外計算開銷。對于即便是相同的編碼方法，由于編/解碼算法的不同，可能計算效率的差異較大。由于在計算機系統中，最終的編碼運算都會反映為一些二進制運算，因而研究者通常使用編碼需要的總的二進制異或運算次數來衡量由于額外冗余編碼帶來的系統計算開銷。對于一個隨機存取的存儲系統來說，隨機小塊信息寫操作的性能尤為重要。編碼運算中每個單元所參與的平均異或次數可以用來衡量這一指標，我們稱其為編碼的更新復雜度。

綜合上面討論，存儲系統容錯編碼問題可以歸結為尋求對如下指標進行優化的編碼方法

系統滿足需要的容錯性能，容錯數為k的系統。

系統有較小(或最優)的冗余度

系統有較小(或最優)的編碼/更新復雜度。

2 線性編碼

對于單容錯系統來說，簡單的奇偶校驗即可使得上面的3個指標達到最優。經典的系統都是使用的這種方法。然而對于k大于1的情況，問題的解決就不是那么簡單了。從通信編碼理論的豐富成果中，兩種比較有代表性的編碼方法被人們挑選出來，并用于解決存儲容錯問題，他們是二進制線性碼和RS碼。

2.1 多維陣列碼

圖1所示是二維陣列編碼及校驗矩陣。二維陣列碼是奇偶校驗的自然推廣，由圖1很容易看出它是雙容錯的。二維陣列碼保持了單容錯時奇偶校驗碼的最優編碼復雜度的特性，但是二維陣列碼的冗余度不再是最優的了。

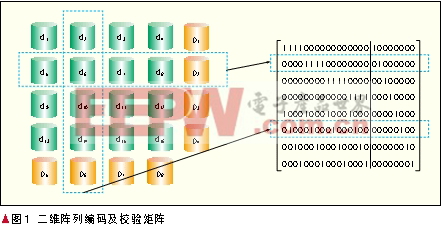
二維陣列碼也很容易推廣為k維陣列。并且容易得到這樣編碼的k容錯特性。但是隨著k的增大，冗余會越來越大[2-3]。

2.2 Full碼

圖2所示是FULL-2碼。FULL-2碼可看做是二維陣列碼的推廣。

FULL碼依然保持了最優的編碼復雜度，并且冗余度要比陣列碼好很多。然而不幸的是，當k大于3時，FULL-k碼不再是k容錯的[4]。

2.3 RS碼

圖3所示是RS碼的校驗矩陣。RS碼從最佳的冗余特性出發。達到Singleton界的RS碼被人們提出并廣泛應用。

校驗矩陣通過線性變換可以化為系統矩陣，用存儲系統的語言亦可顯式地區分出系統中哪些單元用于存儲校驗單元。可以看出，矩陣中的元素不再是“0”、“1”，而為有限域元素的冪，故編碼需要使用有限域運算。在計算機系統中，有限域元素最后還是會被映射為“0”、“1”單元。這時每個有限域元素一般會被映射為多個“0”、“1”單元，而有限域運算也可以被分解為這些“0”、“1”單元的復雜運算。我們仍然以編碼所需的異或運算為基本單位，則編碼所需的異或運算次數和編碼算法的巧妙程度有關。目前較好的域運算算法所需的異或次數大約為O(n3)[5]，計算復雜度相當高。RS碼是MDS碼，故冗余度是最優的。