摘要：著重分析了兩輪自平衡小車的設計原理與控制算法，采用卡爾曼濾波算法融合陀螺儀與加速度計信號，得到系統姿態傾角與角速度最優估計值，通過雙閉環數字PID 算法實現系統的自平衡控制。設計了以MPU-6050傳感器為姿態感知的兩輪自平衡小車系統，選用8位單片機HT66FU50A為控制核心處理器，完成對傳感器信號的采集處理、車身控制以及人機交互的設計，實現小車自主控制平衡狀態、運行速度以及轉向角度大小等功能。

引言

　　兩輪自平衡小車一般都是以倒立擺的結構模型為基礎，是移動機器人研究中的一個重要領域，是一個非線性、強耦合、多變量和不穩定的動態系統，可以很好地驗證控制理論及控制方法的優秀平臺，具有很高的研究價值^[1]。

　　平衡車論文普遍側重理論研究^[2]，首先建立直立車體的運動學和動力學數學模型(Euler-Lagran方法)，設計反饋控制器來保證車體的平衡(極點配置和LQR兩種算法)，在此基礎上進行基于LabVIEW的計算及仿真，或者基于Matlab搭建控制系統模型，給定參數，顯示機器人的運動仿真圖和系統響應曲線，獲得兩種算法的最優反饋矩陣，系數K對應圖1四個電位器實時修正。

　　本文的側重點是理論與實踐結合，硬件電路設計、軟件設計與調試。其中，傳感器數據融合與電機控制PID算法是實現小車平衡的核心內容，硬件設計結合關鍵源代碼分析是本文的亮點。

　　平衡車設計過程中一般是整定PID，難點是如何運用仿真模擬車體平衡的參數，換算不同系數，將控制器設計實施到實際的設計當中。

1 基本工作原理

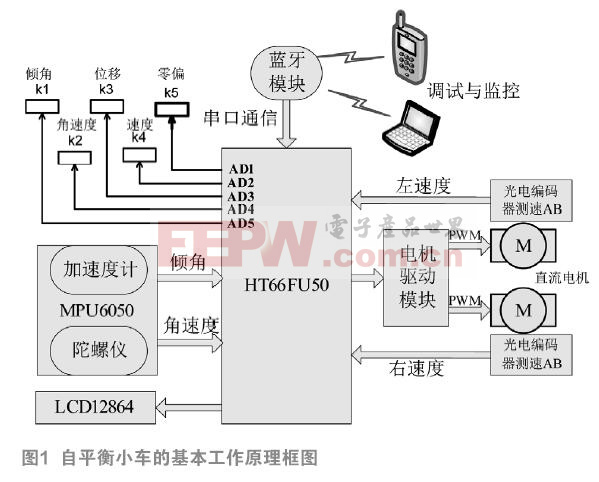
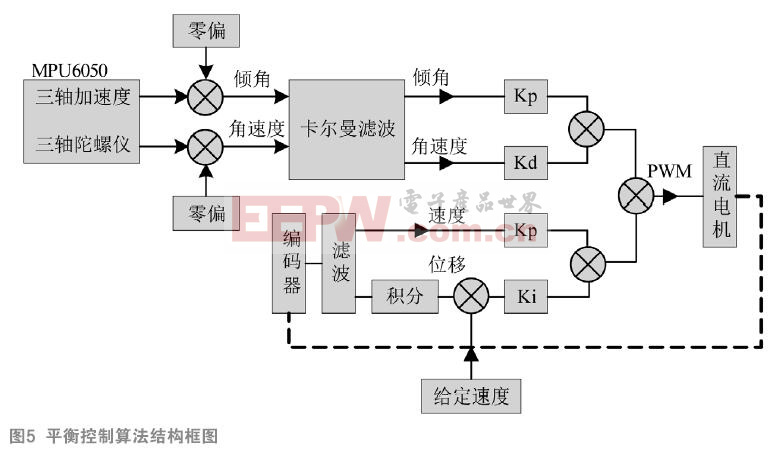
　　利用HT66FU50微控制器，使用PID 閉環控制算法和卡爾曼濾波算法完成數據融合處理，得到平滑而穩定車體控制值，通過電機驅動模塊來驅動電機產生前進或后退的加速度來控制車體保持平衡，同時系統還要根據速度的反饋量來完成對車體速度和方向的控制。通過藍牙模塊與外部設備連接來控制小車的運動狀態。自平衡小車的基本原理框圖如圖1所示。

2 加速度傳感器及其源代碼分析

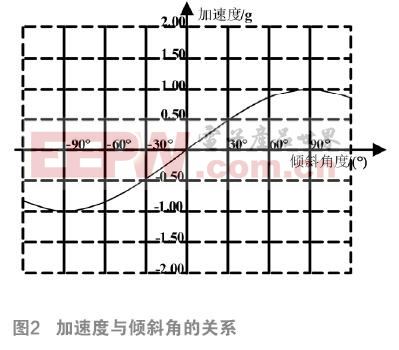
　　加速度傳感器的輸出=地球重力(1g)×傾斜角的正弦(sin)(如圖2)。當傾斜角接近90°時，相對角度變化加速度傳感器的輸出變化就會越來越小。將加速度傳感器的輸出換算成傾斜角度時需使用反正弦函數arcsin。

　　根據單軸加速度求角度(含弧度換算)：

　　Accel=arcsin(A_x)*180/π (1)

　　Ax加速度傳感器的輸出值，Accel傾斜角X軸。單軸求角度范圍為+90°~-90°，超出部分出錯，因此，程序要限幅，1≤Ax≤-1。

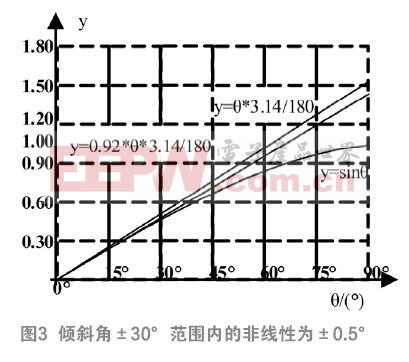
　　如圖3(y=sinθ)，若傾斜角接近±30°的話，傾斜角與傳感器輸出的關系就會接近正比例關系，就沒必要取正弦函數進行計算了。

　　Accel≈k*A_x*180/π (2)

　　當系數取0.92時，角度范圍可以擴大到-45°~+45°。

　　2條檢測軸需要相互正交，并且都與旋轉軸垂直，隨著一個軸的靈敏度下降，另一個軸的靈敏度會上升，通過使用雙軸加速度傳感器就能精確測量傾斜角。雙軸求角度范圍為+180° ~-180°，通過公式(3)計算得到。

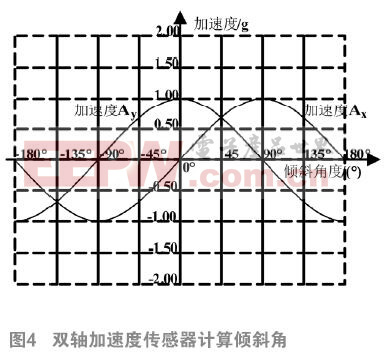
　　Accel=arctan(A_x/A_y)*180/π (3)

　　A_x與A_y加速度傳感器的輸出值，Accel傾斜角。

　　關鍵源代碼如下：

　　//加速度范圍為±2g時，換算關系：16384 LSB/g，角度較小時，也可以采用近似x=sinx得到角度(弧度), deg = rad*180/3.14。

　　Accel_x= GetData(ACCEL_XOUT_H);

　　//讀取X軸加速度

　　Angle_ax = (Accel_x - 800) /16384;

　　//去除零點偏移800，計算得到加速度g

　　Angle_ax = asin(Angle_ax)*180/3.14;

　　//Angle_ax = Angle_ax*180/3.14;

　　//反正弦求角度，而后弧度轉換為度

　　//傾斜角與arctan(Ax/Ay)成正比(如圖4)

　　// acc = atan2(Ax,Ay)*180/π

　　//角速度范圍為2000deg/s時，換算關系16.4 LSB/(deg/s)

　　Gyro_y = GetData(Gyro_Yout_H);

　　//靜止時角速度Y軸輸出為-80左右，去除偏移

　　Gyro_y = -(Gyro_y + 80)/16.4;

　　//去零點偏移，計算角速度值，負號為方向處理

　　Kalman_Filter(Angle_ax,Gyro_y);

　　//執行卡爾曼濾波，平滑角度與角速度。

3 卡爾曼濾波及其源代碼分析

　　卡爾曼濾波器可分為：時間更新方程和測量更新方程。時間更新方程也可視為預估方程，測量更新方程可視為校正方程。根據上一狀態的估計值和當前狀態的觀測值推出當前狀態的估計值。

　　卡爾曼濾波標識：ˉ代表先驗，^代表估計。如表1所示，對于角度估算，先預測，可以近似認為是上一時刻的角度值加上此刻陀螺儀測得的角速度值乘以時間，因為。通過重力加速度來矯正陀螺儀的角度漂移^[7]，即為多傳感器數據處理，通俗稱為“數據融合”。

　　卡爾曼方程1：先驗估計。

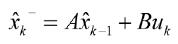(4)

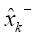先驗估計值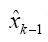，前次運算估計值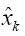，后驗估計值(算后數值，也是再次換算的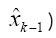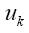，為此刻陀螺儀測的角速度的值。A與B是系統參數。

　　卡爾曼方程4：由觀測變量z_k，更新估計。

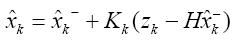(5)

　　為卡爾曼增益，對應源代碼中的K_0 、K_1，z_k就是此刻測得角度Accel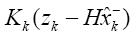，是測得角度與先驗估計的誤差比較，對應源代碼中的Angle_err。

　　部分源代碼如下：

　　float Q_angle=0.001; //初始值

　　float Q_gyro=0.003;

　　float R_angle=0.5;

　　char code C_0 = 1;

　　void Kalman_Filter(float Accel,float Gyro)

　　{

　　//Accel角度(由加速度計求得角度)

　　//Gyro角速度(陀螺儀測得角速度)

　　Angle= Angle +(Gyro - Q_bias) * dt;

　　…

　　…

　　…

　　Angle_err = Accel - Angle;//誤差

　　Angle = Angle + K_0 * Angle_err;/

　　Q_bias = Q_bias + K_1 * Angle_err; /

　　Gyro_x = Gyro - Q_bias;

　　// Angle誤差與卡爾曼增益來修正后的角度

　　// Q_bias誤差與卡爾曼增益來修正偏移

　　// Gyro_x卡爾曼修正后的角速度

　　}

　　理解卡爾曼濾波方程1：

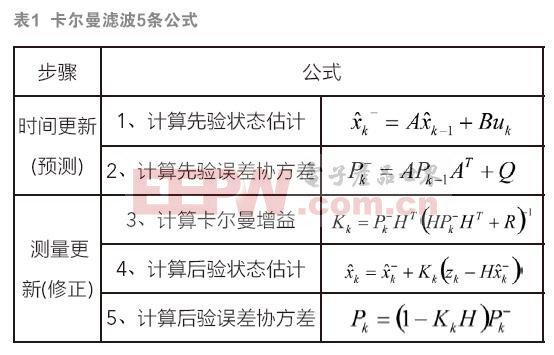
　　等號左邊Angle為此刻的角度預測值，等號右邊Angle為上一時刻的值，Gyro為陀螺儀測的角速度的值，dt是兩次濾波之間的時間間隔， Q_bias是上一時刻陀螺儀靜態偏移量。(Gyro-Q_bias)*dt就是當前狀態的觀測值。陀螺儀有個靜態漂移，而且還是變化的，計算時要除去。

　　陀螺儀與加速度經過卡爾曼濾波前后波形的優劣比較，采用上位機調試工具(串口虛擬示波器)Serial_Digital_Scope V2實時觀察，參考文獻[4]，本文略。

4 電機控制PID算法

　　數字式PID控制算法可以分為直接計算法(也稱位置式PID)和增量計算法。所謂增量計算法就是相對于標準算法的相鄰兩次運算之差，得到的結果為增量。

　　位置式PID算法如下：

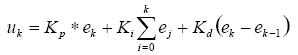
　　其中k是采樣序號，k=0，1，2，……;

u_k是k第次采樣時刻的計算機輸出值;

e_k是k第次采樣時刻輸入的偏差值;

e_k-1是k-1第次采樣時刻輸入的偏差值;

k_i是積分系數，;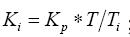

k_d是微分系數，。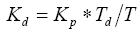

　　Arduino平衡車的PID代碼如下：

　　Output = kp * error+ki * errSum+kd * dErr

　　電機PWM控制數據，靜止過程的平衡，為角度與角速度采用PD算法;行駛過程的平衡，為速度與位移采用PI算法[4]。

　　PWM1 =Angle_Kp* Angle + Angle_Kd*Gyro_x;

　　Angle反映傾角，Gyro_x反映快慢。Angle_Kd是微分控制，具有超前性，他的控制是和偏差輸入的變化率有關，也就是角速度。

　　PWM2 =moto_Kp* speed + moto_Kpn* position;

　　speed為速度，position為n次速度的累積，理解為速度的積分(位移)，moto_Kpn為積分系數[6]，慎重調節。此處系數代號，編者特意不寫moto_Ki，根據PID系數的公式，應為累積偏差系數。諸多文獻前后系數倒置，如文獻[6];文獻[1]解釋為D系數;文獻[5]，文字解釋透徹，但論文圖中PID系數與源代碼有不符。

　　最終控制參數PWM = PWM1+ PWM2，也就是雙閉環PID控制。

　　Angle_Kp、Angle_Kd、moto_Kp、moto_Kpn對應四個電位器(如圖1)，經過單片機ADC轉換，可以實時PID系數的調節，可以由上位機或者液晶監控數據。

　　PID調參步驟：

　　首先，程序內置PWM2=0;

　　第二，設定D=0，逐漸增加P，當車體出現震蕩，加入D，當出現抖動，增加P，反復調節P、D即可實現直立;

　　第三，加入PWM2，先P由小變到大，觀察各次響應，直至得到反應快、超調小的響應，再調節積分控制作用I參數來消除控制穩態誤差。

　　電機轉速和位移值計算，關鍵源代碼如下：

　　speed_dot=(speed_real_LH+speed_real_RH)*0.5;

　　// speed_dot為此時左右車輪速度，求平均

　　speed *=0.85; //車輪速度濾波，k-1時刻取值

　　speed += speed _dot*0.15;//車輪速度濾波+k時

　　position+=speed; //速度的累積

　　position+=Speed_Need; // Speed_Need給定速度

本文來源于中國科技期刊《電子產品世界》2016年第2期第51頁，歡迎您寫論文時引用，并注明出處。