基于Gabor小波與RBF神經網絡的人臉識別新方法
加入技術交流群
人臉識別是人類最杰出的認知能力之一，讓汁算機具有人的智能，使它可以象人類一樣辨認人，一直是眾多計算機科學工作者追求的目標。人臉識別作為一種應用前景十分廣泛的身份鑒別方法，是模式識別領域極富挑戰性的一個熱點研究問題。
人臉圖像由于受光照、表情以及姿態等因素的影響，同一個人的臉像矩陣差異也比較大，人臉識別所選取的特征必須對上述因素具備一定的穩定性和不變性。Gabor小波是Gabor變換與小波理論相結合的產物，它繼承了小波變換的多分辨率特性，同時具有GaborN數本身所具有的局域性和方向性。VD Malsburg小組最先將Gabor小波引入人臉識別領域，應用Gabor小波與彈性圖匹配技術相結合取得了良好的識別效果。Gabor小波核函數具有與哺育動物大腦皮層簡單細胞的二維反射區相同的特性，即具有較強的空間位置和方向選擇性，并且能夠捕捉對應于空間和頻率的局部結構信息；Gabor濾波器對于圖像的亮度和對比度變化以及人臉姿態變化具有較強的健壯性，并且它表達的是對人臉識別最為有用的局部特征。
提高神經網絡的泛化能力問題是RBF網絡的一個重要研究方向。目前，提高網絡泛化能力的研究主要集中在如何選取恰當的網絡規模，即網絡結構設計問題上。關于RBFN絡結構設計，一個公認的指導原則是Moody準則，即：在沒有其它先驗知識的情況下，與給定樣本一致的規模最小的網絡就是最好的選擇。
本文充分利用人臉特征矢量的相對分布信息，提出了一種新的聚類初始化方法，能使RBFN絡逼近于Moody準則下的最優結構，從而保證該網絡具有較好的泛化能力。由于在隱層參數固定的條件下，線性方程組的最小二乘解就是全局最優解，所以本文采用混合學習算法：由線性最小二乘法計算隱層和輸出層之間的連接權值，由梯度下降法調整隱層神經元的中心和寬度。這種方法與單純采用梯度下降法相比，學習速度更快，而且可以避免局部極小值問題。同時提出了一種有效的學習速率估算方法，使得RBF網絡的整個學習過程具備自適應能力。
2 基于Gabor小波的人臉特征提取
2．1 構造Gabor小波
Gabor小波核函數定義如下：
上式表示一個經過高斯包絡調制過的正弦波，其中
控制高斯窗口的寬度以及正弦波的波長，φ控制整個濾波器的方向，改變φ可以對濾波器進行旋轉，σ為高斯窗的寬度與正弦波的波長之比。ψk經過平移、旋轉和尺度變化形成一個自相似的函數族，即Gabor濾波器組。
對于數字圖像，需要把參數k的模||k||和方向參數φ進行離散化，通常在5個對數空間頻率v∈{0…，4}8個方向μ∈{0，…，7}上采樣。針對人臉圖像本文通過實驗確定在2個空問頻率v∈{1，2}和8個方向μ∈{0，…，7}上進行采樣，形成16個Gabor濾波器。
2．2 人臉圖像Gabor濾波
將人臉灰度圖像插值為128×128(記為I)，再分別與各個Gabor濾波器進行卷積，得到人臉圖像的Gabor小波表示：
稱Oμ，v(z)為Gabor人臉，其中z=(x，y)為相對于頻譜中心的相對坐標值。通過二維快速傅立葉變換，將時域卷積變換為頻域乘積運算以提高計算速度。
2．3 小波分解降維
每幅Gabor人臉圖像Oμ，v(z)都是與I(z)同樣大小的復數矩陣，取其幅值系數作為特征。通過參數μ，v的變化，Oμ，v(z)表達不同頻率和方向的人臉特征信息，將一幅人臉的全部Gabor特征組成矢量，則人臉的原始特征數據高達262144維，后續處理非常困難。ChenKiun Liu分別取采樣因子ρ=4，16,64進行下采樣處理，所得識別結果相差很小，所以采樣法最低可以得到4096維。而小波變換是一種常用的圖像壓縮方法，與采樣法相比具有能量和信息損失小的優點。Harmon指出16×16的圖像對于人臉識別是最基本的。因而，本文對Gabor人臉進行3次小波分解，將其低頻近似圖按行連接起來組成列矢量，并將全部列矢量依次連接起來，即為一幅人臉的低維Gabor特征列矢量。
2．4 主分量分析
設n為訓練樣本數目，Xi表示第i幅人臉圖像的L維Gabor特征列矢量，則訓練樣本集的總體散布矩陣表示為：
式中
為樣本均值。由于St為實對稱矩陣(L×L)，可將St化成對角形
的特征值，P為正交變換矩陣，且特征值均非負值，令λ1≥λ2≥…λL≥0，λl對應的正交歸一化特征向量為ul，則u1，u2，…，uL可以構成RL空間的一組標準正交基，在該正交特征空間中，人臉樣本Xi可以表示為：
選用前r(rL)個較大特征值對應的特征向量作為正交基底(主分量)，將Xi向該正交空間的子空間投影則有：
得到Pi=xi(1)，xi(2)，…，xi(r)為一組坐標系數，代表了Xi在新特征子空間中的位置，可將r維投影系數Pi作為人臉特征矢量輸入分類器進行識別。
3 基于RBF神經網絡的分類器設計
RBF神經網絡的結構如圖1所示，它是一種三層前向網絡，其中r、u和s分別為輸入層、隱層和輸出層的節點數。
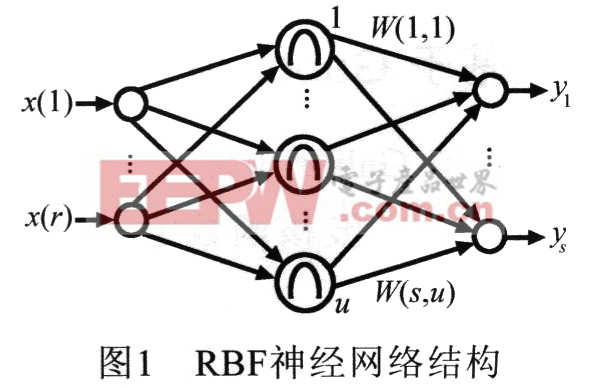
為隱層第k個神經元的中心，則隱層節點k的輸出為：
式中||?||表示歐氏范數。當RBF選用高斯核函數時，其輸出為：
式中σk為隱層第k個神經元的寬度。輸出層第j個節點的輸出值yj為：
式中W(j，k)為隱層節點k到第j個輸出節點的連接權值。
3．1 RBF網絡初始化
RBF神經網絡可看作是從特征子空間到類的映射，因此輸入層的節點數與輸入特征矢量的維數r相等，輸出層的節點數就是待分類樣本的類別數。隱層節點的選取是一個開放的問題，在理想情況下，隱層節點數取得最小值為樣本類別數。每個人最多對應2～3個隱層節點，隱層聚類的初始化過程如下：
1)先假設每人收斂于一個聚類中心，將隱層節點數初始化為輸出層節點數。
2)隱層第k個神經元的中心Ck為k類特征矢量的均值。
3)計算k類各個樣本到中心Ck的距離，以最遠點Pk(f)到中心的距離作為σk的初值。
4)計算各個聚類中心j到聚類中心k的距離：
其中，最小距離為：
根據dmin(k，l)與dk，dl的關系，可將k類分為如下幾種情況：
a)若dk+dl≤dmin(k，l)，則k類與其它類沒有重疊，如圖2(a)所示；
b)若dk+dl>dmin(k，l)，則k類與其它類相交。進一步分為兩種情況：
i)dk一dldmin(k，l)，如圖2(b)所示；
ii)dk一dl≥dmin(k，l)，如圖2(c)所示，表示k類包含其它類，可能導致RBF神經網絡分類錯誤。
5)對每類樣本，依次按照以下兩個規則進行判別并細分：
i)包含規則：若dk+dl>dmin(k，l)且dk一dl≥dmin(k，l)，則k類包含其它類，必須將k類細分為兩個聚類；
ii)正確歸類規則：若k類包含其它類樣本的個數大于1，必須將k類細分為兩個聚類。
評論