- 1.有了Fourier,為什么還需要Wavelet? 先來揭揭短: (1)Fourier分析不能刻畫時間域上信號的局部特性。 (2)Fourier分析對突變和非平穩信號的效果不好,沒有時頻分析。 傅立葉變換將函數投影到正弦波上,將函數分解成了不同頻率的正弦波,這不能不說是一個偉大的發現,但是在大量的應用中,傅立葉變換的局限性卻日趨明顯,事實上在光滑平穩信號的表示中,傅立葉基已經達到了近似最優表示,但是日常生活中的信號卻并不是一直光滑的,而且奇異是平凡的,傅立葉在奇異點的表現就著實讓人不爽,從方
- 關鍵字:
小波 Fourier
- 上一小節中我們介紹了函數項級數的概念,這一節我們來討論函數項級數的性質。傅立葉級數是一種函數項(三角函數)級數,本質上來說,一幅圖像(或者一組信號)就是一個函數,我們研究圖像的傅立葉變換,就是要探討如何將圖像函數用三角函數進行展開。所以如果要徹底搞清楚傅里葉變換,那么討論函數項級數的性質是非常有必要的。在此基礎上,我們將引入傅立葉級數的概念。 如果你對本文涉及的基礎問題不甚了解,那么建議你閱讀本文前面的部分。希望讀者能日積月累,夯實基礎。 完全搞懂傅里葉變換和小波(1)——總綱 http://w
- 關鍵字:
傅立葉級數 小波
- 1.4 傅立葉級數展開 之前我們在介紹泰勒展開式的時候提到過傅立葉級數。利用傅立葉級數對函數進行展開相比于泰勒展開式,會具有更好的整體逼近性,而且對函數的光滑性也不再有苛刻的要求。傅立葉級數是傅立葉變換的基礎,傅立葉變換是數字信號處理(特別是圖像處理)中非常重要的一種手段。遺憾的是,很多人讀者并不能較為輕松地將傅立葉變換同高等數學中講到的傅立葉級數聯系起來。本節我們就來解開讀者心中的疑惑。 如果你對本文涉及的基礎問題不甚了解,那么建議你閱讀本文前面的部分。希望讀者能日積月累,夯實基礎。
- 關鍵字:
傅里葉變換 小波
- 這一系列的文章中間中斷了很久,很多朋友也留言希望我繼續連載完,遂“重拾舊河山”,希望如果有時間能夠把它做完。 本節我們介紹歐拉公式,它是復變函數中非常重要的一個定理,同時對于傅立葉變換的理解也必不可少。我們在高等數學里學習的傅立葉級數通常都是用三角函數形式表示的,而傅立葉變換中的一般都是用冪指數形式的,歐拉公式的作用正是把三角函數與e的冪指數聯系到一起。 如果你對本文涉及的基礎問題不甚了解,那么建議你閱讀本文前面的部分。 完全搞懂傅里葉變換和小波(1)——總綱 http://www.eepw.
- 關鍵字:
傅里葉變換 小波
- 書接上文,之前我們介紹了高等數學里的三個中值定理,本節我們繼續按照總綱的思路,用柯西中值定理來證明泰勒公式。這是我們循序漸進引出傅里葉的最后一項任務,完成這一步的學習之后,你就可以從級數的角度,了解傅里葉的意義了。 完全搞懂傅里葉變換和小波(1)——總綱 http://www.j9360.com/article/201703/344766.htm 完全搞懂傅里葉變換和小波(2)——三個中值定理 http://www.j9360.com/article/201702/344594.htm
- 關鍵字:
傅里葉變換 小波
- 書接上文,本文章是該系列的第二篇,按照總綱中給出的框架,本節介紹三個中值定理,包括它們的證明及幾何意義。這三個中值定理是高等數學中非常基礎的部分,如果讀者對于高數的內容已經非常了解,大可跳過此部分。當然如果你需要對傅里葉變換有一個更深刻的認識,或者說從數學角度一點一滴完全搞懂它,為了體系的完整性,這部分知識還是必須的。 上篇文章鏈接地址:完全搞懂傅里葉變換和小波(1)——總綱 http://www.j9360.com/article/201702/344594.htm 由于公式較多,這里只能
- 關鍵字:
傅里葉變換 小波
- 無論是學習信號處理,還是做圖像、音視頻處理方面的研究,你永遠避不開的一個內容,就是傅里葉變換和小波。但是這兩個東西其實并不容易弄懂,或者說其實是非常抽象和晦澀的! 完全搞懂傅里葉變換和小波,你至少需要知道哪些預備知識?主頁君從今天開始就將通過一些列文章告訴你他們之間的來龍去脈!本節是全部系列文章的第一節——總綱,日后我們也將按照這個思路一點一點講述所有的知識。需要說明的是,本文主要面向計算機專業或者電子信息專業的讀者,為此我們將盡量采取一些非常非常基礎的知識來幫助你理解。所以,題目里面講的“完全搞懂
- 關鍵字:
傅里葉變換 小波
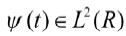
- 本文首先分析了基于小波變換圖像壓縮原理、流程和方法,然后針對傳統的嵌入式小波零樹壓縮編碼算法的不足,提出了改進方案。改進方案包括使用正交小波基Z97替代小波變換,使用排除法減少對重要系數的掃描次數,使用多種掃描順序替換單一的“Z”字型掃描等。仿真實驗結果表明,改進的方案提高了圖像壓縮效率,改善了重構圖像的質量。
- 關鍵字:
小波 圖像 壓縮 算法 EZM 201607
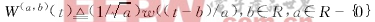
- 本文描述了基于正交小波函數族的多址通信原理,并提出了一種多速率正交小波調制方法.用具有不同伸縮尺度的小波函數對不同信道中的碼流進行編碼,可以達到擴展信息序列頻譜的目的,因此這一多址技術具有很好的抗干擾性
- 關鍵字:
原理 及其 應用 通信 函數 正交 小波 基于
- 摘要:小波變換在電力系統諧波中的應用,與諧波本身的特性是直接相關的,要得到實時性和精確性都較高的檢測效果就需要時電力系統的諧波特點,小波在這方面的應用原理有深刻的理解。文中對此在作了深入分析的基礎上,
- 關鍵字:
檢測 研究 諧波 電力系統 小波 變換 基于
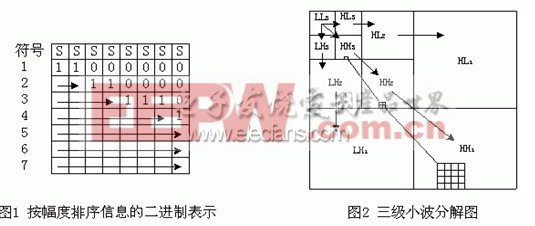
- 嵌入式零樹小波EZW編碼及其算法改進,在基于小波變換的圖象壓縮方案中,嵌入式零樹小波 EZW(Embedded Zerotree Wavelets)[1]編碼很好地利用小波系數的特性使得輸出的碼流具有嵌入特性。近年來,在對EZW改進的基礎上,提出了許多新的性能更好的算法,如多級樹
- 關鍵字:
算法 改進 及其 編碼 小波 EZW 嵌入式

- DM642上5/3提升小波的優化,在新的圖像壓縮標準JPEG2000中,采用9/7、5/3提升小波變換作為編碼算法,其中5/3小波變換是一種可逆的整數變換,可以實現無損或有損的圖像壓縮。在通用的DSP芯片上實現該算法具有很好的可擴展性、可升級性與易維護性
- 關鍵字:
優化 小波 提升 5/3 DM642
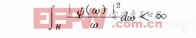
- 快速小波變換的定點DSP實現,小波變換具有良好的時——頻局部性,是分析奇異信號的重要方法。定點DSP在工程中的應用十分普遍,具有低成本,高性能的特點。利用DSP實現小波變換可以滿足工程是實時性的要求。文中簡要介紹了小波變換理論
- 關鍵字:
DSP 實現 定點 變換 小波 快速
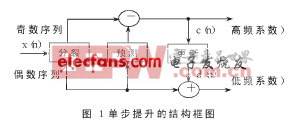
- 圖像的二維提升小波變換的FPGA實現,小波分析理論以其良好的時頻區域性和多分辨率分析能力,開辟了圖像處理的嶄新領域。小波變換是一種很好的圖像分解方法,非常適合于分析突變信號而用于靜止圖像邊緣的提取和壓縮。高階小波變化還可以用于實時處理視頻
- 關鍵字:
FPGA 實現 變換 小波 二維 提升 圖像
- 摘要:文中在應用對數域電路的基礎上,提出了一種新型的連續小波變換方法,它通過對母小波的一種數值逼近得到小波函數的有理公式,并以Marr小波為例來模擬這個逼近過程,并用Matlab對逼近過程進行仿真。仿真結果顯示
- 關鍵字:
變換 實現 小波 濾波器 SI 基于
小波介紹
您好,目前還沒有人創建詞條小波!
歡迎您創建該詞條,闡述對小波的理解,并與今后在此搜索小波的朋友們分享。
創建詞條
關于我們 -
廣告服務 -
企業會員服務 -
網站地圖 -
聯系我們 -
征稿 -
友情鏈接 -
手機EEPW
Copyright ?2000-2015 ELECTRONIC ENGINEERING & PRODUCT WORLD. All rights reserved.
《電子產品世界》雜志社 版權所有 北京東曉國際技術信息咨詢有限公司

京ICP備12027778號-2 北京市公安局備案:1101082052 京公網安備11010802012473