高速公路宏觀動態交通流模型以交通流的集總行為為研究對象，描述了交通流的空間分布及隨時間變化的規律，能較精確地描述高速公路交通流的真實行為，不僅是交通自動控制系統設計、分析、仿真決策的基礎，也是交通預報和評價某些交通設施設計所需要的。其中，希臘學者Markos Papageorgiou所提出的Papageorgiou模型，能夠以較小的計算量和滿意的精度描述車道數目單一、出入匝道無特大流量沖擊的高速公路交通狀況而廣泛應用。

對交通流模型進行在線仿真，或驗證某算法對實際道路的控制效果時，有時由于交通數據龐大或控制算法過于復雜，往往消耗大量機時。尤其在外場環境下操作，工控機不僅體積、功耗龐大，還易出現工作失常的現象，在交通控制的實際應用中表現欠佳。FPGA技術高速、低成本、小型化的優勢使其理論研究與實際應用成為炙手可熱的研究課題，目前已經完全具備數據運算、信息處理、濾波計算等功能，常常使一些原來比較難解決的技術瓶頸得以輕松實現，從而使產品的可移植性增強，開發周期大為縮短，性價比大幅提高，同時FPGA可以實現純硬件浮點運算功能，克服定點數據對高精度、數據范圍較大的運算無能為力的缺陷，更適合科學與工程計算。因此本文采用浮點數在FPGA上實現Papa georgiou模型的仿真。

1 高速公路交通流宏觀動態模型

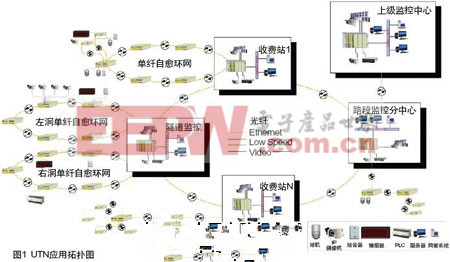
宏觀動態交通流模型又稱為交通流連續介質模型，它通過對單向運動的交通流在某時刻t在某一位置x的有關變量來把握交通的本質。各研究組織所提出多種形式交通流模型，其間主要差別在于交通流量、車輛平均速度和車流密度的關系的表征，以及上下游交通相互作用的描述形式。為了簡化模型使其便于應用在實際中，通常根據高速公路幾何形狀和交通狀態將其劃分成若干路段，路段可不等距劃分，但應保證每段路段車道數目相同，至多有一個入口、一個出口，每個路段的幾何形狀大致相似，每個路段內的交通狀態近似均一，Papageorgiou模型也采用如圖1所示的分段方式：

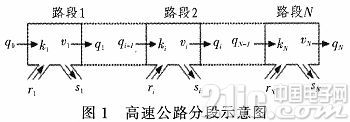
基于上述高速公路的分段方式，其數學表達式如式(1)～(4)所示：

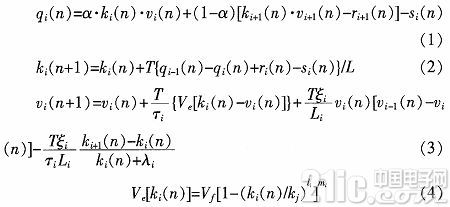
式(1)～(4)分別是動態流量模型、動態交通流密度模型、動態速度模型和速一密關系模型，各符號含義見文獻。上述模型涉及到了加減乘除及冪運算，目前Quartus II中有公開的浮點數運算IP核可實現加減乘除運算，但式(4)中出現有底數、指數可能均為浮點數的冪運算。本文根據所選參數進行多項式擬合，將所有運算均限定在加減乘除的浮點數運算范圍內。

2 16位自定義浮點數數據格式

Quartus II軟件自帶的IP核的輸入輸出數據采用IEEE754單精度32位浮點數格式，其數據結構表示如下：

其中S為1位符號位，E為8位階碼位，M為尾數的24位小數位。調用QuartusII浮點數運算IP核實現加減乘除的操作，其資源消耗依次為加減運算消耗LE單元個數均為1 497，消耗嵌入式乘法器個數均為0：乘除運算消耗LE單元個數分別為809、3345，消耗嵌入式乘法器個數分別為0、7。對一個路段進行仿真時，至少需要6次加法、7次減法、12次乘法、4次除法，僅實現加減乘除運算所消耗FPGA邏輯資源已蔚為壯觀，若要仿真多個路段，將付出巨大的硬件成本，甚至無法實現，因此本文在IEEE754浮點數格式的基礎上采用自定義16位浮點數格式，編寫浮點運算模塊，盡量減少FPGA資源的消耗，其數據結構為：

其中S為1位符號位，E為6位階碼位，M為尾數的9位小數位，隱藏整數位1，其表示的數據值下式所示：

上式中，當S為0時，A為正數，當S為1時，A為負數;E-31為浮點數的指數，指數可在2-31到231之間變化;尾數采用原碼表示，整數部分1為缺省值，不在上述格式中表示;0在上述格式中，階碼和尾數均為0，符號位可以是任意值。為方便說明自定義浮點數的運算過程，設有兩個浮點數是a和b，其數據格式如式(6)所示。

2.1 自定義16位浮點數加法和減法運算

浮點數加、減法的操作過程相似，流程圖如圖2所示。

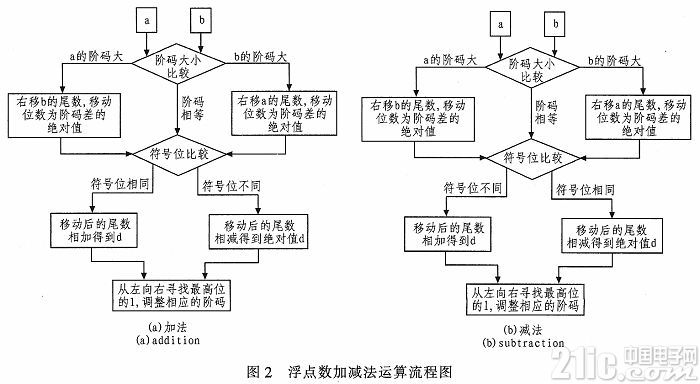
1)對階操作：在兩數尾數的小數部分的高位補1，比較兩數的階碼是否相同。若相同，直接進入第2)步;若不同，比較兩個數的階碼大小，令階碼小的尾數連同高位補的1向右移位，右移的尾數等于階差的絕對值;

2)符號位操作：加法運算，若兩數符號相同，則符號位同兩加數;若兩加數符號相異，符號位由絕對值較大的加數決定。減法運算，被減數和減數的符號相異，則兩數的絕對值相加;兩數符號相同，則兩數相減再取絕對值。結果的符號位取被減數的符號位(當被減數的絕對值較大時)或者是減數的符號位取反(當減數的絕對值較大時);

3)歸一化操作：若步驟1)和2)所得結果為非規格化數，找出運算結果的最高位1，由高至低依次將其后部分存入最終結果，階碼做相應的調整。

2.2 自定義16位浮點數乘法和除法運算

浮點數的乘法運算按照以下步驟進行，其算法流程圖如圖3所示。

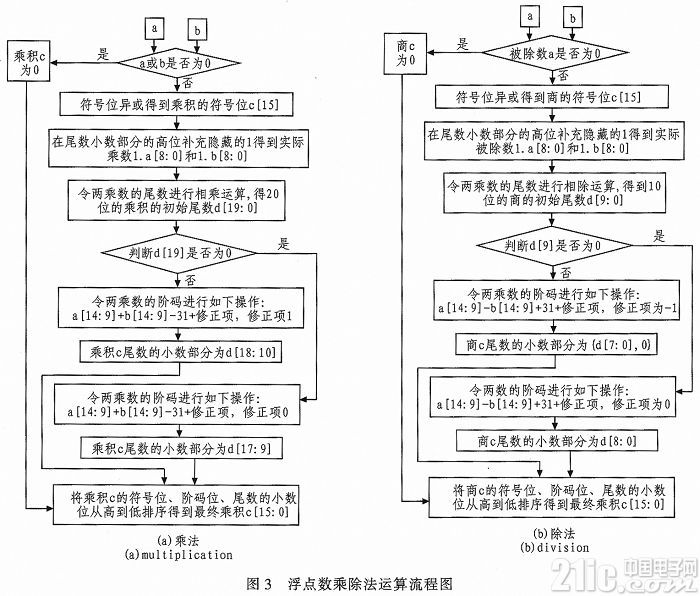
1)判0操作：乘法運算，檢查兩乘數是否有0，若有，結果為0。除法運算，檢查被除數是否為0，若為0，結果為0。

2)符號位操作：對兩數的符號位進行異或操作，確定結果的符號位。

3)階碼操作：乘法運算，乘積的階碼是(Ea+Eb-31+修正項);除法運算，商的階碼是(Ea-Eb+31+修正項)。修正項的值由4)中非規格化數調整為規格化數進行的移位個數決定。

4)尾數操作：乘法運算，兩乘數尾數的小數部分的高位補1后相乘，得到乘積的20位初始尾數d;除法運算，被除數和除數尾數的小數部分的高位均補1，對1.Ma和1.Mb進行相除操作，令d=1.Ma÷1.Mb，采用移位相減，先比較1.Ma和1.Mb大小，若1.Ma≥1.Mb，則d為1，且令1.Ma=1.Ma-l.Mb;若1.Ma1.Mb，則d為0，且令1.Ma左移一位再次進行比較得到d，依次重復上述比較過程最終得到商的初始尾數d。

5)歸一化操作：乘法運算，d[19]、d[18]不同時為0，若d[19]為0，即乘積的整數為01，則乘積尾數的小數部分為d[17：9]，修正項為0;若d[19]為1，即乘積的整數為10或11，則將初始尾數右移一位，同時乘積指數加1，修正項為1，乘積尾數小數部分為d[18：10]。除法運算，d[9]和d[8]不會同時為0，若d[9]不為0，商的商的初始尾數的整數為1，尾數小數部分為d[8：0];若d[19]為0，商的初始尾數的整數為0，則將初始尾數左移一位，同時商的階碼減1，修正項為-1，商的尾數小數部分為d[7：0]并在低位補0。

將上述操作結束后得到的符號位、階碼位、尾數的小數部分按照自定義浮點數格式進行排列，得到最終的結果。

3 自定義浮點數運算的仿真機綜合分析

為了驗證本文中自定義浮點數運算模塊的正確性及其誤差大小，且考慮到仿真模型中的變量都為正的浮點數，這里以實數7.8和5.6為例，分別將其變換為本文中自定義的浮點數格式，在自行開發的以EP3C80E484C型號為核心的FPGA上運行，并通過QuartusⅡ軟件中自帶的debug工具軟件查看其運算結果，其中加減乘除運算的部分結果如圖4所示。

為了驗證FPGA實際運算結果的正確性，將上述浮點數格式的結果轉換成十進制格式，并進行系統誤差對比，如表2所示。

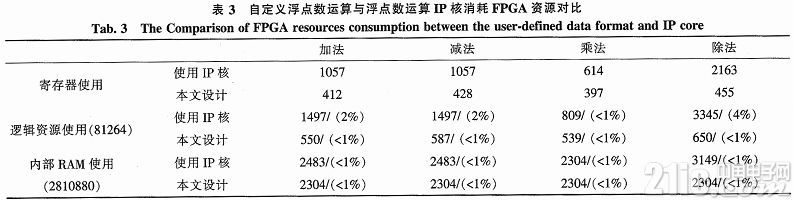
由表2的對比結果可知，在FPGA運行的16位自定義數據格式的加、減、乘、除運算模塊的計算誤差不超過0.1%，能夠滿足宏觀交通流模型的仿真中對計算精度的要求。此外，在保證模型仿真精度的同時，自定義16位數據格式的加、減、乘、除運算模塊與Quartus II軟件公開的32位浮點數運算IP核相比，能夠顯著降低對FPGA資源的消耗，其資源對比如表3所示。

4 模型仿真及綜合分析

基于自定義浮點數運算模塊，前文以Papageorgiou模型為仿真對象，在FPGA上設計了交通流仿真模塊。以一段長度為5 km的單向單車道的高速公路為例，將其等分為10段，采用時間設為T=15 s，模型中其他參數設置為：α=0.95，ζ=1，l=1.86，m=4.05，τ=0.005 56 h，ζ=35 km2/h，λ=40 veh/km/lane，Vf=95.1 km/h，kj=110veh/km/ lane。

在初始時刻，假設各路段密度、速度相同，分別為60 veh/km/lane、30 km/h，并假定駛入高速公路的車流量為恒值Q0=1 500 veh/h，每個入口匝道車流量也為恒值r=750 veh/h。

在FPGA上對高速公路宏觀模型進行仿真需要注意兩個問題：1)邊界賦值問題，這里采用邊緣賦值條件，令v0(n)=v1(n)，k0(n)=Q0/v1(n)，k11(n)=k10(n);2)通過多項式擬合方法簡化式(4)中指數和底數均為浮點數的冪運算，并由(7)式進行替換。

Ve[ki(n)]=0.008[ki(n)]3-0.064[ki(n)]2+0.371 4[ki(n)]+92.310 3 (7)

FPGA實現的模型仿真結果如圖5所示。

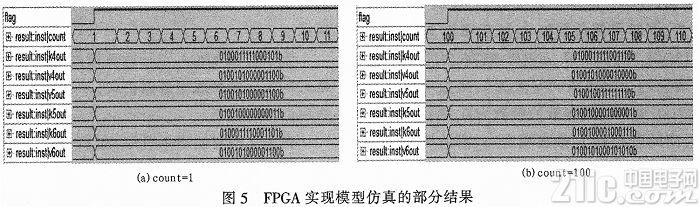
其中flag表示結果輸出標志，count是仿真時間間隔的個數，k5out-k6out和v5out-v6out別是第5、6路段的交通流密度和車輛平均速度。為查驗FPGA的仿真精度，選取count= 1，100時兩組數據，轉換成十進制浮點數形式，與MATLABA仿真結果對比，如表4所示。

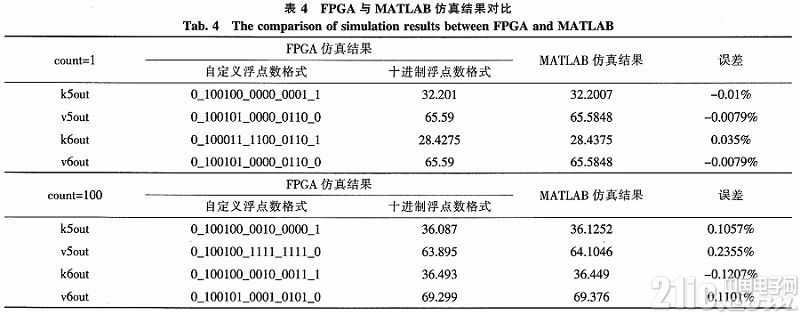
從表4知，基于FPGA的模型仿真與MATLAB的仿真結果對比，在仿真初期誤差幾乎為0，隨著仿真時間持續增長，誤差隨之增大，但總體差距不大，能夠滿足仿真精度的要求。

5 結束語

1)本文設計了基于自定義浮點數的高速公路交通流宏觀動態模型仿真，并在自行開發的FPGA電路板上進行了驗證，其中自定義浮點數運算實現簡單，節省了FPGA邏輯資源，能夠在保證計算精度的前提下以較快的速度實現模型的仿真，在后續的交通控制研究中可以進一步在FPGA上實現控制算法的效果驗證;

2)本文的不足之處在于沒有直接實現底數和指數全為浮點數的冪運算，而是根據所設定的參數進行多項式擬合，導致模型仿真精度在一定程度上受到擬合精度的限制。