一種RBF神經網絡的自適應學習算法
引言
徑向基函數(Radial Basis Function,RBF)神經網絡具有結構簡單,學習速度快等優點,在函數逼近、系統辨識、模式識別等領域得到了廣泛應用。
構造RBF網絡的關鍵是合理選取徑向基函數的數量和中心向量。目前,比較常用的方法主要有K均值聚類法、C-Means算法等。這些方法都是在人為確定徑向基函數的數量和初始向量之后,采用基于歐氏距離的最近鄰方法來實現聚類的。對于類間距離大,類內距離小的樣本可以得到比較不錯的結果,而對于類間交錯較大,類內距離大的情形,這種方法的分類能力將嚴重減弱,從而不利于網絡的泛化應用。另外,網絡的訓練過程和工作過程完全獨立,如果外部環境發生變化,系統的特性會隨之發生變化,由此需要重新對網絡進行訓練,這使問題變得更加復雜,也使網絡的應用領域受到限制。
針對以上算法存在的問題,本文提出了一種RBF網絡的自適應學習算法。該算法事先不需要確定RBF的數量和中心向量,而是在學習過程中,根據誤差在輸入空間的分布,自適應地增加RBF的數量,并適當調節中心向量。為了不使RBF的數量過于膨脹,還制定了相應的刪除策略,該策略通過綜合評價每個RBF對網絡所作的貢獻,然后刪除貢獻小的RBF,使網絡結構始終保持簡潔。
1 RBF神經網絡
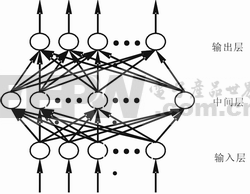
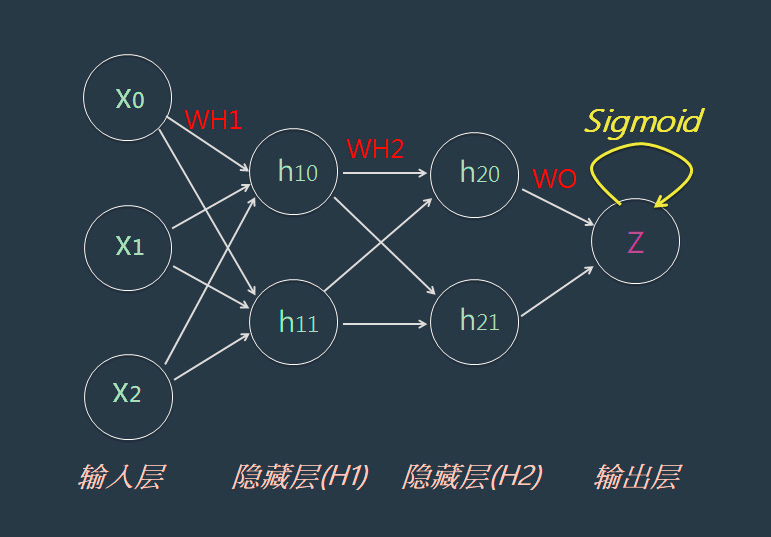
RBF網絡是一種三層前饋網絡,由輸入層、輸出層和隱層組成。其中,輸入層和輸出層皆由線性神經元組成;隱層的激活函數(核函數)采用中心徑向對稱衰減的非負非線性函數,其作用是對輸入信號在局部產生響應。輸入層與隱層之間的權值固定為1,只有隱層與輸出層之間的權值可調。
設輸入矢量x=(x1,x2,…,xn)T,隱層節點個數為m,RBF網絡的輸出可表示為:
![]()
式中:ωi是第i個隱層節點與輸出層之間的權值;φi(‖x—ci‖),i=1,2,…,m為隱層激活函數。通常采用如下高斯函數:
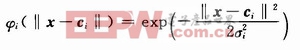
式中:σi和ci分別表示該隱層節點的寬度和中心矢量;‖·‖是歐氏范數。
2 RBF網絡自適應學習算法
RBF選取得越多,網絡的逼近精度越高,但同時也會使網絡的泛化能力下降,因此,在滿足一定逼近精度的條件下,應選取盡可能少的中心向量,以保證網絡有較好的泛化能力。本文提出的算法,根據網絡的輸出誤差在輸入空間的非均勻分布,以及每個RBF對網絡所作貢獻的大小,通過相應的添加和刪除策略對網絡參數進行自適應調整,使網絡的逼近性能和泛化能力都達到較高的要求。同時,網絡的訓練和工作可以交替進行,所以它能夠適應外界環境的緩慢變化。
2.1 添加策略
添加策略綜合考慮了網絡輸出誤差在輸入空間的非均勻分布。需要統計每個輸入矢量產生的輸出誤差,然后通過比較找出誤差相對較大的點,再在這些點附近適當地插入隱層節點。
設(xk,yk),k=1,2,…,N是一組訓練樣本,初始時刻,隱層節點數為零,每次執行添加操作,依據以下準則判斷是否添加隱層節點:
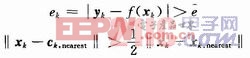
式中:![]() 是網絡輸出均方誤差;ck,nearest和xk,nearest分別對應與輸入向量xk最接近的隱層節點中心和輸入向量。如果滿足添加條件,則將(xk+xk,nearest)/2設為新的隱層節點中心,將ek設為新節點的權值,中心寬度取
是網絡輸出均方誤差;ck,nearest和xk,nearest分別對應與輸入向量xk最接近的隱層節點中心和輸入向量。如果滿足添加條件,則將(xk+xk,nearest)/2設為新的隱層節點中心,將ek設為新節點的權值,中心寬度取![]() 。
。
2.2 刪除策略
由于RBF神經網絡是一種局部感知場網絡,網絡總的輸出取決于隱層與輸出層之間的權值和隱層節點中心與輸入矢量之間的距離。進行訓練時,所選取的訓練樣本相對比較稀疏。當某一個隱層節點中心離每一個輸入矢量都很遠時,即使其權值是一個較大的數,也不會對輸出產生太大的影響。在訓練結束后進行檢驗的過程中,檢驗的數據一般都比較密集,若某些輸入矢量離該隱層中心較近,則輸出會受到很大的影響,這使網絡的泛化能力變差。因此需要制定一種策略來刪除這樣的隱層節點,由此引入了刪除策略。
刪除策略是針對每個隱層節點對整個網絡所作貢獻的大小不同而提出的。貢獻大的節點,繼續保留;貢獻小的節點,則刪除。對任意隱層節點i,用Ai來表示它對整個網絡所作的貢獻。Ai定義為:

執行刪除操作前,先對Ai進行歸一化處理,即![]() 。最后的判斷規則為:若
。最后的判斷規則為:若![]() ,則刪除第i個隱層節點,其中θ為判決門限。
,則刪除第i個隱層節點,其中θ為判決門限。
在采用梯度下降法調整隱層節點中心位置和權值的過程中,需要計算每個輸入矢量對應的輸出誤差ek,以及每個隱層節點的輸出值φ(‖xk-ci‖)。而執行添加和刪除操作時也需要計算ek和φ(‖xk-ci‖)。為了減小計算量,提高運算效率,可以在調整隱層的中心位置和權值的過程中先保存ek和φ(‖xk-ci‖)的值。
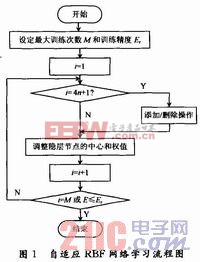
2.3 算法流程
自適應RBF神經網絡學習算法的具體流程如圖1所示。對RBF進行訓練之前,先確定最大訓練次數M和訓練允許誤差Er,作為訓練結束的條件。









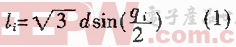
評論