摘要：可逆邏輯電路能大幅度降低能耗，越來越受到研究人員重視。運用可逆邏輯電路對傳統脈沖分配器進行可逆設計，并提供了物理實現方法。首先對傳統的脈沖分配器中的觸發器和計數器進行可逆設計，然后將傳統脈沖分配器的中的計數器進行替換，最后將可逆計數器和譯碼器級聯，從而構建可逆脈沖分配器。仿真結果表明實現了脈沖分配器的功能。
關鍵詞：可逆邏輯電路；D觸發器；可逆脈沖分配器；電子波導Y-分支開關

隨著集成電路規模的增加，其能耗問題已經愈發引起研究者的注意。Bennett最早證明能耗來源于計算過程中的不可逆操作，傳統數字電路由于不可逆計算導致信息的擦除導致能量的消耗，Landauer指出，每一個信息位的丟失對應KT*Ln2焦耳的熱量產生，式中K是波爾茲曼常量，T是絕對溫度。雖然單個信息位散失能量很少，但對于超大規模集成電路，功耗不能忽略。如果組成電路的所有門均能夠執行可逆計算，即不存在信息位的擦除，理論上可以實現集成電路的零損耗。目前廣泛研究的量子運算是一種具體的可逆計算，即能夠從根本上解決集成電路功耗問題。
量子計算可以由可逆邏輯電路實現．現有的研究對可逆邏輯電路研究很多，但大都集中在可逆組合邏輯電路方面，時序邏輯電路方面研究的比較少，文獻首次提出了可逆觸發器的設計方法，但沒有考慮電路的性能指標。文獻提出了可逆主從觸發器的設計方法。文獻設計了對數式移位寄存器設計方法，但是僅能適用于此類寄存器。現在沒有通用的設計方法可以適用不同種類的可逆時序邏輯電路設計。
針對可逆邏輯電路現有的問題，提出了一種方法，將傳統的不可逆時序邏輯電路轉化為可逆時序邏輯電路。并且以典型的可逆時序邏輯電路中的脈沖分配器的設計方為例，設計了可逆脈沖分配器，通過將不可逆脈沖分配器中的基本邏輯門替換成可逆邏輯門，達到將不可逆時序電路轉換為可逆時序電路的目的。

1 可逆邏輯電路的基本概念
量子計算機中，信息的基本單元是量子比特，即量子位，信息的基本操作元件是可逆邏輯門。量子比特是信息的載體，量子比特的信息經可逆邏輯門操作處理后，最后得到計算結果。
定義1組成可逆邏輯電路的基本單元必須是可逆邏輯門，并且還需要滿足以下約束條件：1)電路中無扇人扇出操作，2)輸入與輸出位數相等，3)對應電路真值表滿足一一映射。
定義2任何一個較復雜的可逆邏輯門均是由或基本可逆邏輯門構成。量子代價用來衡量一個量可逆邏輯電路的復雜性，用實現一個可逆邏輯電路所需要的或者基本可逆邏輯門的數量表示，不管內部結構如何，一個基本可逆邏輯門的量子損耗是1。
定義3在可逆邏輯電路中，除期望輸出外的剩余輸出稱為垃圾位。垃圾位是無用輸出位，也是電路能耗產生的根源。因此垃圾位數量的多少是評價可逆邏輯電路的一個最重要的性能指標。當添加垃圾位輸出后，為使量子可逆邏輯電路的輸入輸出位數相等，需在輸入端添加一定數量的常量輸入，常量輸入的位數也影響到可逆邏輯電路綜合的量子代價，常量輸入取0或1。
常用可逆邏輯門如圖1所示。

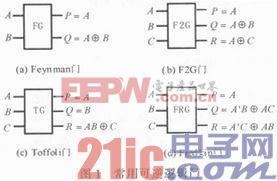
Feynman門(FG門)有兩個輸入量子比特，分別是控制量子比特和目標量子比特。它所實現的功能為當控制量子比特為0時，目標量子比特不變；而當控制量子比特為1時，目標量子比特將反轉。FG門的線路如圖1(a)所示。其中，P、Q為FG門的兩個輸出量子比特，FG門能夠實現線路的復制功能。當B=0時，可得到兩個相同的輸出A。因此，FG門能夠實現可逆邏輯量子比特的復制。
F2G門又叫做Feynman Double gate(F2G)，有3個輸入比特，能完成輸入比特的兩位復制。
FRG門，又稱受控交換門，是一種三輸入輸出的可逆邏輯門，如圖所示。當控制端為0時，FRG為三輸入輸出的直通門，即P=A、Q=B、R=C。當控制端A輸入信號為1時，P=A，Q=C，R=B。
TG門是最常用的多比特可逆邏輯門，輸入位由兩個控制比特位和一個被控比特來構建符合特定要求的可逆邏輯電路。此外，門可以通過修改控制位數量，構成具有不同數量控制位TG門系列，以此來構建符合特定要求的可逆邏輯電路。