引言

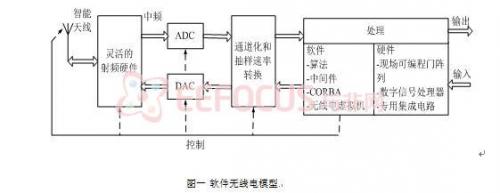
　　數字控制振蕩器 (NCO) 在軟件無線電(SDR)通信系統中具有重要的作用，是軟件無線電數字變頻技術的必要組成部分，它的性能很大程度上決定著數字變頻模塊性能以及載波同步模塊的同步效果。在軟件無線電通信中，信號的處理往往都集中在離散數字域內進行，數據的傳輸速率和信號的質量都要非常高，這樣就要求數字控制振蕩器必須具有頻率分辨率高、頻率轉換速度快、無雜散動態范圍值(SFDR)高、頻譜純度高和生成的正、余弦信號保持良好的正交特性等特點。

　　數控振蕩器主要由相位累加器、量化器、相位幅度轉換電路等部分組成。相位累加器將相位按頻率控制字的步長累加，累加結果與初始相位(即相位偏移)的和作為量化器的輸入，量化器截取前M bits作為相位幅度轉換電路的輸入，最后，相位幅度轉換電路根據相位值輸出對應的正弦或余弦值。本文通過對傳統CORDIC算法實現數控振蕩器存在的問題進行分析，提出一種適用于軟件無線電通信系統的數控振蕩器實現新方法。該方法利用二階泰勒(Taylor)級數近似和殘余相角補償的方法來解決CORDIC算法實現時的精度不夠的缺陷，提高了數控振蕩器的輸出信號頻譜的純度;整個設計采用流水線結構從而可以保證系統的高速度，滿足軟件無線電系統的高速數據處理的要求;在相位累加器部分加入相角抖動模塊來改善角度周期性截斷誤差所引起的雜散，進一步提高數控振蕩器的無雜散動態值。

　　傳統CORDIC算法實現

　　CORDIC(Coordinate Rotation Digital Computer)算法是由J.Voider等人在1959年提出的[1]，它是基于向量旋轉的算法，通過迭代方法實現對任意角度的向量旋轉，這些迭代只需使用簡單的移位和加減法操作，所有三角函數都可以通過向量旋轉函數進行計算。CORDIC算法的基本迭代算式為：

　　用CORDIC算法實現數控振蕩器存在精度不高的問題，它的雜散源主要有以下幾部分：由于算法采用的算術精度有限對最終結果造成的誤差，這部分誤差是由尾數舍棄帶來的截斷誤差，這部分誤差是引起雜散的一個原因;N次旋轉所得的累加角度與目標角度之間的殘余相角誤差所引起雜散;由于CORDIC算法的迭代級數有限，旋轉產生的角度誤差為周期信號，周期性誤差同樣會引起雜散。

　　由于傳統CORDIC算法實現數控振蕩器存在著不足，故本文在傳統CORDIC算法的基礎上，提出采用Taylor級數補償CORDIC算法的改進數控振蕩器實現方法。