二階泰勒補償實現的原理如下：假設相位累加器輸出的相角 為N bits的，把相角 分成三部分，即N=j+k+2。由于CORDIC能計算相角的范圍為[-99.9°, 99.9°]之間，這是由CORDIC算法本身所決定的，這樣就必須通過三角關系把輸入相角轉換到[-99.9°, 99.9°]之間，本文利用輸入相角的高兩位來判斷相角的轉換。然后再把接下的(N-2)bits的數據分成j bits和k bits兩部分，中間j bits作為CORDIC的輸入相角 ，后k bits作為后續二階泰勒補償模塊的輸入數據。在這里并沒有把整個(N-2)bits的角度 作為CORDIC的輸入，而是只取了前j bits，這樣就會很大程度的降低模塊的占用資源，同時，減少輸入數據的位寬就會減少迭代的次數。由于這樣只取 的高 1位作為CORDIC的輸入，這樣產生的截斷舍入誤差會影響到整個數控振蕩器的SFDR，為了補償這部分的損失，本文采取二階泰勒級數來補償這部分損失，對于低k bits的角度(-)用來作為二階泰勒級數補償的輸入相角。利用二階泰勒級數補償(公式8)，可以計算出比較準確的正余弦值。

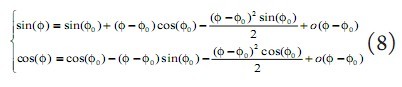
　　仿真結果

　　為了驗證結果有可比性，驗證性能時采用無雜散動態范圍值(SFDR)這一公認指標進行衡量。在頻域中，SFDR是衡量一個信號失真特性的有效方法，SFDR為定義在一定頻率范圍內的信號與第二大頻率成分的功率差。在驗證性能時，用Matlab對基于CORDIC算法的改進數控振蕩器進行仿真，在仿真時采取了定點化仿真，輸入相位位數為22bits，輸出的正余弦值的位寬為20bits，對于本文提的方法的具體參數設定如下：CORDIC的輸入位寬k=10bits，累加器位寬N=22bits，采樣頻率，輸出正余弦信號的頻率，仿真的結果如圖2(b)所示，從圖中可以看出本文提出的方法的SFDR值可以達到114.5dB，輸出信號的頻譜能量主要集中在10MHz附近，但第二大頻率成分的尖峰出現0Hz附近，這個尖峰是未補償盡殘余雜散頻譜，它與主頻譜幅度相差近115dB，對數控振蕩器的性能影響很小。并且，隨著累加器位寬和輸出信號位寬的增加，數控振蕩器的SFDR值會進一步提高，本文的實現方法在輸出正余弦值位寬為24bits時，它的SFDR值可以達到134dB。

　　圖2(a)所示的是基于傳統CORDIC算法實現的數控振蕩器，它的SFDR值達到66.5dB。從圖2可以看出改進方法提高SFDR值近48dB。本文的改進方法與其他的實現方法的性能比較見表1，從表中可以看出本文提出的改進方法比參考文獻提出的實現方法的輸出信號SFDR值都要高，所以，本文提出的方法輸出信號頻譜的純度要優于其他方法。