一種基于遺傳算法的時間表問題求解算法
時間表問題又稱課表問題,就是解決對時間和空間資源爭奪而引發沖突。20世紀70年代中期,美國S.Even等人論證了課表問題是NP完全類問題。理論和時間表明,只要課表所涉及的任何信息量稍有變化,就會導致課表編排選擇方案的劇增,即“組合爆炸”。一般作法是針對具體的應用環境,忽略一些限制條件,但這樣會造成使用效果的不理想。本文中提出利用特定條件對課程與教室分批,采用遺傳算法對時間表問題進行求解,給出了編碼形式、遺傳算子規則及適應度函數,通過對某學校課表編排數據的計算,驗證了算法的有效性。對時間表問題的優化求解,起到一定的效果。
本文引用地址:http://www.j9360.com/article/89970.htm1 課表編排問題的描述


結合上述課表編排的4個條件,課表問題就轉化為二部復圖Hb(V,E)的匹配問題。
2 課表編排問題的遺傳算法
遺傳算法是基于生物的進化與選擇機制的優化算法。遺傳算法通過維持一個群體,并按個體的適應度的大小重復的進行選擇。交叉和變異等操作來實現群體內個體結構的重組,將性能良好的解結構遺傳下去,提高后代的適應能力,從而進化到最優或次優解。遺傳算法的基本步驟:確定編碼方案,確定適應函數,確定選擇策略,控制參數的選擇,遺傳算子的設計,算法終止準則的確定等。
2.1 編碼方案
二進制編碼是最常用的編碼方案,他類似于生物染色體的組成,從而易于用生物遺傳理論來解釋并使得遺傳操作容易表現。且采用二進制編碼時,算法處理的模式數最多。(設采用k進制編碼,碼長為1,則所表示的最大整數為k1,模式數為(k+1)1。可以證明k=2時使得k1=const(常數)時(k+1)1取得最大值)。但該種編碼方案有相鄰整數的二進制編碼可能具有較大的海明距離,如:7和8的二進制表示為:0111,1000。這種缺陷在解決連續化問題時降低搜索效率。故在本問題求解中,采用格雷碼相鄰整數僅有一位不同的特性可克服二進制編碼相鄰證書可能具有較大海明距離的缺陷。他的解碼過程如下:
設有一格雷碼串(bnbn-1…b0)其解碼過程如下:
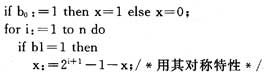
串長為m1×n1,m1為各參數(即課程)的編碼長度;n1為參數的個數(即課程的門數),串中個參數所對應的值為該門課程所選“時間一教室對”集的序號,這樣構造串結構m1最短,故串長也最短。
2.2 控制參數選擇
(1)種群規模N:筆者經過反復實驗發現:N值大進化較慢,但易搜索到全局較優解,而N值小時進化速度快,但不易搜索到較優解,權衡效率和性能,一般N取值為20~100,經過實驗問題N取值為40比較合適。
(2)雜交操作

(3)變異操作
變異算子一般一次只改變一條染色體上的一個基因,比如,染色體Xt=(1,8,3,6,5),變異的基因是第3位,則變異后Xt+1=(1,8,7,6,5)。
2.3 適應度函數
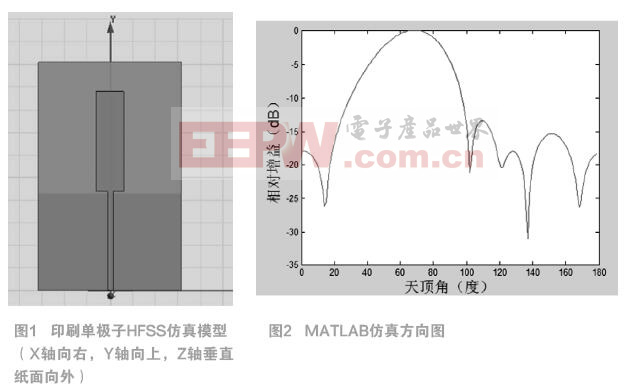
由于課表編排問題是求目標函數最大值,適應度函數定義如下:
其中Wij為第i個體串中對應第j門課所選”時間—教室對”集的權重。Count為第i個個體所對應的各門課程之間的沖突次數。C為一負數,其絕對值足夠大,以致于只要出現一次沖突,該適應只便為負,這樣便于終止準則的選定(因為所求解即要求無任何沖突)。但容易造成各個體間適應值相差過大的情況,所以采用線形排名的選擇策略。終止條件為:
(1)該種群中最大適應值為一正數;
(2)2當前種群中最大適應值與以前各代中最大適應值相差不大,這時說明效果不太顯著,再進化下去沒有必要。
3 實驗結果及結論
本算法用C語言進行驗證,交叉概率均為0.8,變異概率0.2,種群規模設為70。對某學校課表編排數據進行實驗,算法運行2 000代,獲得了滿意的結果,所獲得的時刻表沒有沖突。當算法運行超過4 000代以后,其結果會出現幾處沖突外,但總體結果是比較滿意的。通過手工調整很容易獲得一個一個滿意的時間表。
時間表問題是一個典型的NP完全問題,本文通過對該問題的數學模型的分析,提出以遺傳算法進行求解,算法的運行結果說明了該方法是可行的。實際應用中,還要考慮更多的約束條件,這將是下一步的工作重點。



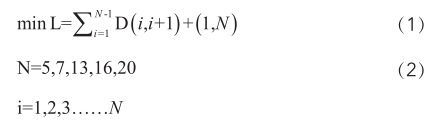

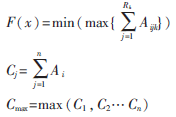
評論