FIR濾波器具有幅度特性可隨意設計、線性相位特性可嚴格精確保證等優點，因此在要求相位線性信道的現代電子系統，如圖像處理、數據傳輸等波形傳遞系統中，具有很大吸引力。本文簡單介紹了其線性相位條件和設計方法，并且提供了一種用DSP實現的方法。

　　一、 引　言

　　在許多信息處理過程中，如對信號的過濾、檢測、預測等，都要廣泛地用到濾波器，而數字濾波器則因其設計靈活、實現方便等特點而廣為接受。

　　所謂數字濾波器就是具有某種選擇性的器件、網絡或以計算機硬件支持的計算程序。其功能本質是按事先設計好的程序，將一組輸入的數字序列通過一定的運算后轉變為另一組輸出的數字序列，從而改變信號的形式和內容，達到對信號加工或濾波以符合技術指標的要求。

　　二、 數字濾波器的兩種類型

　　對于一般的數字濾波器，按照單位沖激響應可分為無限長沖激響應IIR(Infinite Impulse Response)系統和有限長沖激響應FIR(Finite Impulse Response)系統。

　　在IIR系統中，用有理分式表示的系統函數來逼近所需要的頻率響應，即其單位沖激響應h(n)是無限長的;而在FIR系統中，則用一個有理多項式表示的系統函數去逼近所需要的頻率響應，即其單位沖激響應h(n)在有限個n值處不為零。

　　IIR濾波器由于吸收了模擬濾波器的結果，有大量的圖表可查，可以方便、簡單、有效地完成設計，效果很好，但是其相位特性不好控制，必須用全通網絡進行復雜的相位較正，才能實現線性相位特性的要求。

　　FIR濾波器則可在幅度特性隨意設計的同時，保證精確、嚴格的線性相位特性。這在要求相位線性信道的現代電子系統，如圖像處理、數據傳輸等波形傳遞系統中，是具有很大吸引力的。而且，其單位沖激響應是有限長的，不存在不穩定的因素，并且可用因果系統來實現。

　　下面著重討論具有線性相位特性的FIR濾波器。

　　三、 FIR濾波器線性相位特性的條件及設計方法

　　1.線性相位條件

　　為保證濾波器帶內輸出信號的形狀保持不變，常常要求濾波器單位沖激響應h(n)的頻率響應H(ejω)應具有線性的相頻特性，即H(ejω)=H(ω)e-jωk，其中H(ω)為幅頻特性，k為正整數。由傅氏變換的特性可知，線性相位濾波器只是將信號在時域上延遲了k個采樣點，因此不會改變輸入信號的形狀。

　　可以證明，如果濾波器單位沖激響應h(n)為實數，且滿足：偶對稱即h(n)=h(N-1-n)或奇對稱h(n)=-h(N-1-n)時，則其相頻特性一定是線性的。

　　2.設計方法

　　(1) 窗函數設計法

　　從時域出發，把理想的無限長的hd(n)用一定形狀的窗函數截取成有限長的h(n)，以此h(n)來逼近hd(n)，從而使所得到的頻率響應H(ejω)與所要求的理想頻率響應Hd(ejω)相接近。優點是簡單、實用，缺點是截止頻率不易控制。

　　(2) 頻率抽樣設計法

　　從頻域出發，把給定的理想頻率響應Hd(ejω)加以等間隔抽樣，所得到的H(k)作逆離散傅氏變換，從而求得h(n) ，并用與之相對應的頻率響應H(ejω)去逼近理想頻率響應Hd(ejω)。優點是直接在頻域進行設計，便于優化，缺點是截止頻率不能自由取值。

　　(3) 等波紋逼近計算機輔助設計法

　　前面兩種方法雖然在頻率取樣點上的誤差非常小，但在非取樣點處的誤差沿頻率軸不是均勻分布的，而且截止頻率的選擇還受到了不必要的限制。因此又由切比雪夫理論提出了等波紋逼近計算機輔助設計法。它不但能準確地指定通帶和阻帶的邊緣，而且還在一定意義上實現對所期望的頻率響應實行最佳逼近。

　　四、 FIR濾波器的實現

　　不論是窗函數設計法，還是頻率抽樣設計法，都要求出濾波器的單位沖激響應h(n)，然后才能在時域中實現頻域中的濾波。

　　1.濾波系統的差分方程

　　在頻域，當其輸入信號為X(ejω)時，如濾波器的頻率響應為H(ejω)，則其輸出信號為Y(ejω)=X(ejω)H(ejω)。

　　在時域，設濾波器的單位沖激響應h(n)為一N點序列，即0≤n≤N-1時h(n)的值不為零，根據離散傅氏變換的性質，則可以將濾波器的輸入序列x(n)的響應y(n)表示為x(n)與h(n)的卷積和，即：

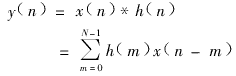
　　這就是濾波系統的差分方程，它給濾波器的實現奠定了理論基礎。即求出時域的h(n)后，便可通過卷積來實現頻域的濾波。