基于FDATool的FIR濾波器設計方法(二)
這一節主要講解一下轉置型FIR濾波器實現。
本文引用地址:http://www.j9360.com/article/249652.htmFIR濾波器的單位沖激響應h(n)可以表示為如下式:
對應轉置型結構的FIR濾波器,如圖1所示,抽頭系數與上一節中講解直接型FIR濾波器的實例相同,濾波器階數為10。

圖1
可以發現轉置型結構不對輸入數據寄存,而是對乘累加后的結果寄存,這樣關鍵路徑上只有1個乘法和1個加法操作,相比于直接型結構,延時縮短了不少。
綜合得到結果如下:
Number of Slice Registers: 1
Number of Slice LUTs: 18
Number of DSP48E1s: 11
Minimum period: 4.854ns{1} (Maximum frequency: 206.016MHz)
關鍵路徑延時報告如圖2所示,其中乘累加操作延時Tdspdck_A_PREG_MULT 2.655ns;另外還有一項net delay居然有1.231ns,如此大是因為fanout=11,仔細研究可以發現在h(n)表達式中x(n)與所有11個抽頭系數進行了乘法操作,因此fanout達到了11,這也是轉置型FIR濾波器的缺點:輸入數據的fanout過大。
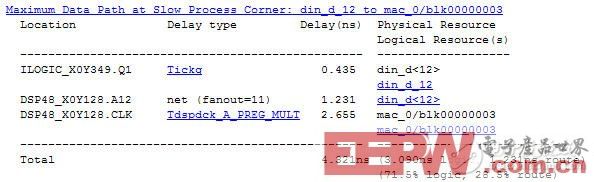
圖2
線性相位:
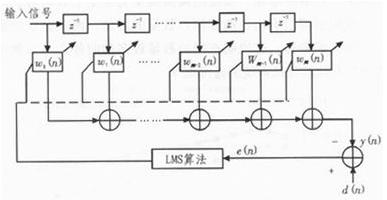
與直接型結構相同,由FIR濾波器的線性相位特征,轉置型結構的FIR濾波器也可優化,如圖3所示為線性相位FIR濾波器轉置型結構,總共11個抽頭系數,其中5對系數兩兩相同,因此可以省去5個乘法器,采用6個DSP資源實現轉置型FIR濾波器。

圖3
流水線實現:
為了進一步縮短關鍵路徑的延時,將乘法器和加法器邏輯分割開,中間加入流水線級,結果如圖4所示,在線性相位結構的基礎上,加入一級寄存器,這樣最大限度上優化時序。
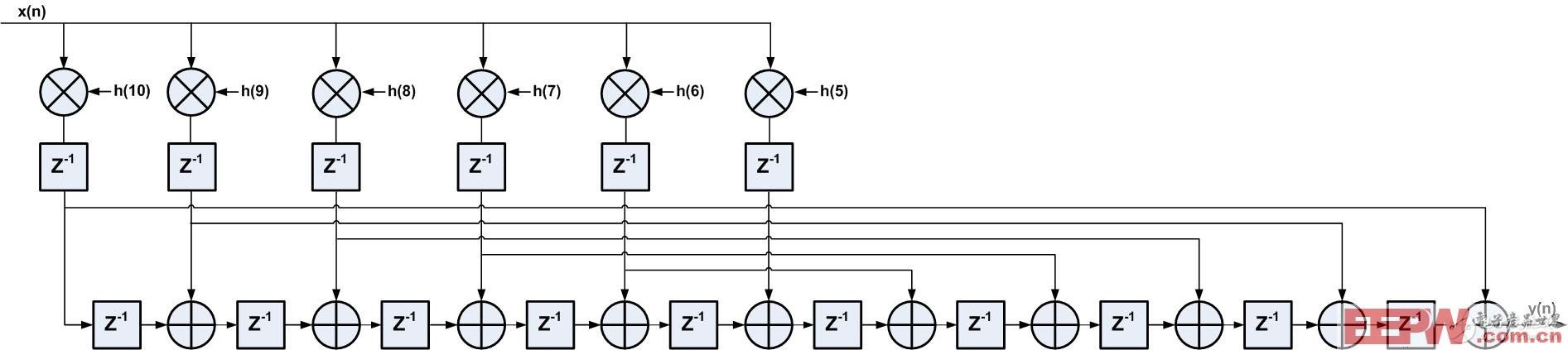
圖4
綜合得到結果如下:
Number of Slice Registers: 355
Number of Slice LUTs: 340
Number of DSP48E1s: 6
Minimum period: 3.861ns{1} (Maximum frequency: 259.000MHz)
如圖5所示為與圖2中相對應路徑的延時報告(圖2由ISE的Timing Analysis工具產生,圖5是由PlanAhead的Timing Analysis工具產生),其中由于采用線性相位結構,輸入信號的fanout只有6,延時從原先的1.231ns減小到1.01ns;并且分隔乘法器和加法器邏輯之后,關鍵路徑上只有乘法器的延時:1.42ns。
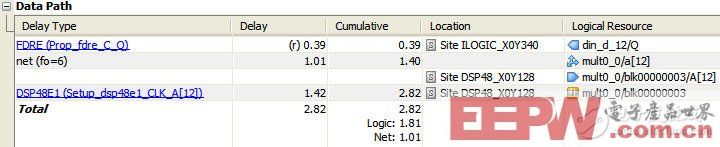
圖5
濾波器相關文章:濾波器原理
濾波器相關文章:濾波器原理
電源濾波器相關文章:電源濾波器原理
數字濾波器相關文章:數字濾波器原理


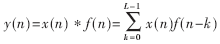
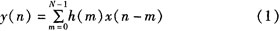
評論