*基金項目：工業(yè)和信息化部2020年產(chǎn)業(yè)技術基礎公共服務平臺—工業(yè)機器人核心關鍵技術驗證與支撐保障服務平臺建設項目（2020-0097-1-1）

現(xiàn)有工業(yè)機器人控制領域，已建立基于機器人全剛性連接假設的機器人動力學模型^[1][2][3]，基于該模型實時引入動力學前饋控制量，可在一定程度上改善系統(tǒng)動態(tài)響應速度，但卻不可避免地導致了系統(tǒng)末端抖動和不穩(wěn)定性^[4]。已有研究表明，機器人系統(tǒng)中的柔性因素（關節(jié)柔性）可影響末端執(zhí)行器的定位精度與運行穩(wěn)定性^[5]，建立考慮機器人柔性因素的動力學模型，對分析確定機器人末端抖動的根源至關重要，同時可為后續(xù)優(yōu)化控制提供基礎^[6]。此外，提高機器人柔順性具有廣闊的應用前景，但柔性動力學模型建立及其控制也存在一定挑戰(zhàn)性^[7]。

本文首先建立了基于Kane 方法的傳統(tǒng)剛性動力學模型，通過對機器人系統(tǒng)的關節(jié)耦合特性進行研究，分析了該模型缺陷和潛在導致系統(tǒng)不穩(wěn)定及末端抖動原因，針對此問題對剛性動力學模型進行改進；考慮關節(jié)柔性因素提出基于Kane 方法的工業(yè)機器人系統(tǒng)柔性動力學模型，旨在更準確反映機器人機電系統(tǒng)的固有特征，提高前饋控制準確性，從而改善系統(tǒng)控制特性。

1   機電系統(tǒng)動力學模型建模方法

理想情況下，機電系統(tǒng)認為是剛性動力學系統(tǒng)，控制如圖1 所示。

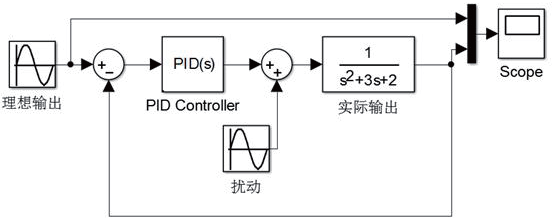
圖1 剛性動力學系統(tǒng)（機電系統(tǒng)）

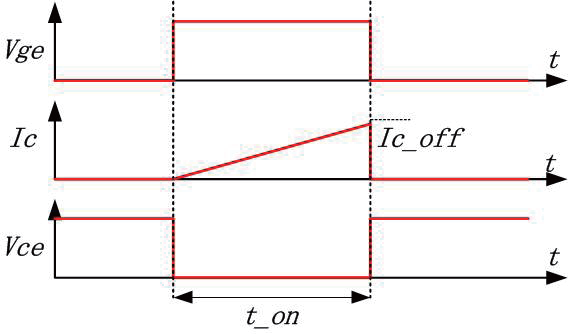
基于剛性動力學模型基礎，根據(jù)圖2 工業(yè)機器人關節(jié)運動狀態(tài)，考慮關節(jié)柔性因素，可改進為柔性動力學模型。

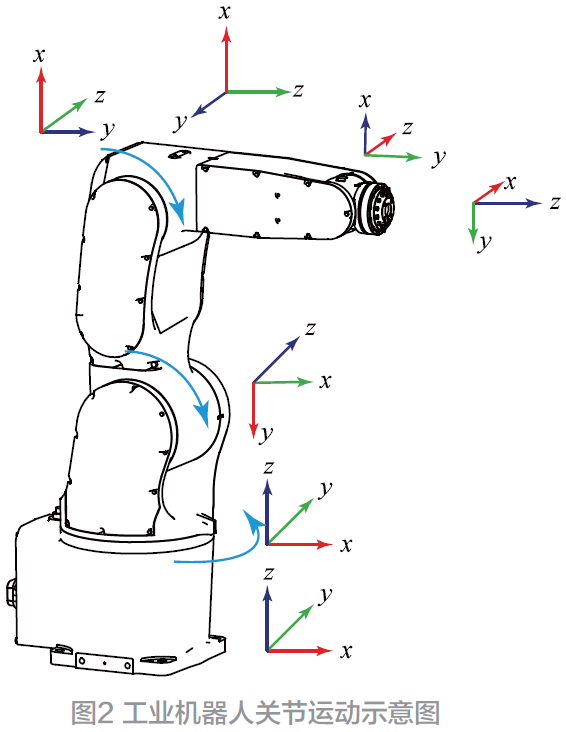
動力學建模目前有許多較為成熟的方法可供使用，較為常用的包括：Newton-Euler 方法；Lagrange 方程；Kane 方法。這些方法思路不同，但均可根據(jù)動力學普遍方程相互轉化，在本文采用Kane 方法進行研究，可建立如下形式方程：

MX+CX+KX=F

2   基于Kane方法的剛性系統(tǒng)模型

2.1 剛性系統(tǒng)模型

Kane 方法基于偏速度與偏角速度的概念，即運動過程中某一位置點與廣義坐標的相對關系。剛性系統(tǒng)的動力學模型可基于各個連桿的廣義主動力與廣義慣性力獲取。

在工業(yè)機器人上選取各個關節(jié)轉角的廣義坐標，將各個連桿的角速度與線速度表示在其坐標系中，構建DH 矩陣：

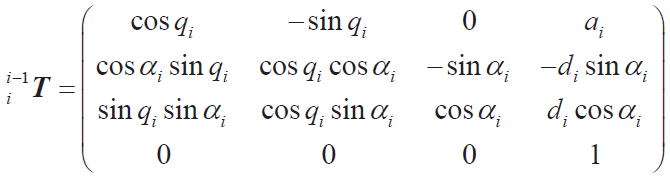
為簡化后續(xù)的分析，在各個連桿上建立固結于連桿的坐標系，并將各個連桿的運動學參數(shù)在局部坐標系中表示。

● 連桿角速度

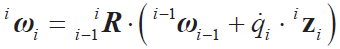
● 連桿角加速度

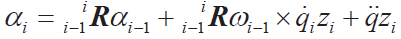
● 連桿線速度

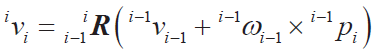
● 連桿線加速度

● 連桿質(zhì)心的速度

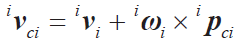
在Kane 方法中，需要引入偏速度的概念

● 連桿偏角速度

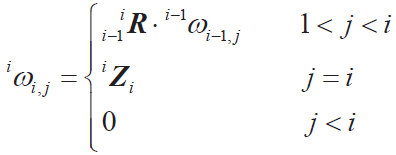
● 連桿偏速度

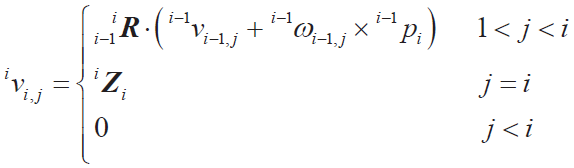
在動力學廣義慣性力為連桿旋轉的慣性力，可表示為：

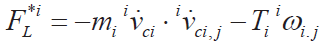
其中，

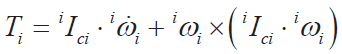
對每一個自由度應用Kane 方程，可得：

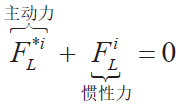
從而可得動力學方程：

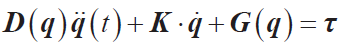
對于剛性模型的動力學方程，q 為電機輸出的轉角，因此關于q 的信息已知，通過給定的運動，可以獲知給定狀態(tài)下的電機扭矩。

剛性動力學模型在給定的關節(jié)轉速下，可以確定末端的位置姿態(tài)以及關節(jié)扭矩，可作為動力學前饋控制基礎，用于提升機器人控制的精度和響應。但由于運動中擾動的存在以及動力學建模中不可避免的誤差，實際的機器人控制系統(tǒng)不能完全依賴于動力學模型，而需要進行實時反饋控制。且理想的剛性連接假設前提下，動力學模型忽略了關節(jié)非線性因素，將引發(fā)機器人系統(tǒng)在部分位姿控制中產(chǎn)生諧振及動態(tài)響應遲滯現(xiàn)象，進而導致系統(tǒng)不穩(wěn)定及末端抖動。

2.2   關節(jié)柔性模型

當考慮關節(jié)柔性時，各個連桿的遞推關系為：

● 連桿角速度

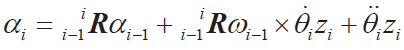
● 連桿線速度

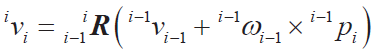
● 連桿線加速度

● 連桿質(zhì)心的速度

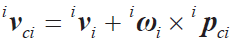
當考慮關節(jié)柔性時，各個連桿的偏速度可表示為：

● 連桿偏角速度

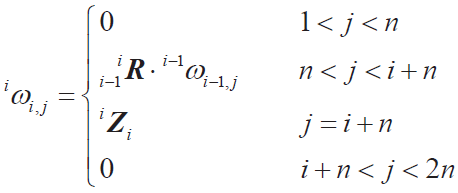
● 連桿偏速度

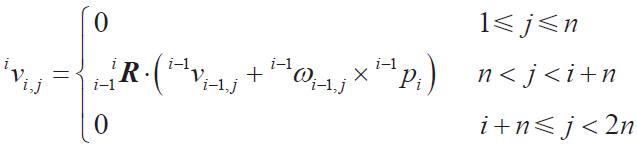
● 連桿質(zhì)心偏速度

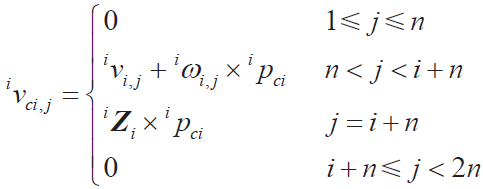
與剛性模型相比，利用Kane 方法得到的各個自由度的方程針對于連桿在彈簧變性后的轉角，針對電機輸出的自由度：

● 廣義慣性力

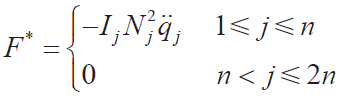
● 廣義主動力

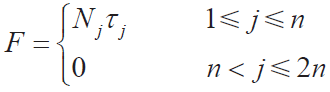
利用Kane 方程可建立考慮關節(jié)柔性系統(tǒng)的動力學模型：

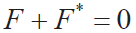
所導出的方程為12 個2 階微分方程，當考慮關節(jié)柔性的影響時，原有的微分方程將轉變?yōu)椋?/p>

此時的微分方程組為時變微分方程，需要進行數(shù)值求解。由該方程的形式可知，該方程為時變非線性微分方程，其系數(shù)矩陣中，質(zhì)量矩陣、阻尼矩陣以及剛度矩陣均為坐標的函數(shù)，這使得該方程難以得到解析解，可以使用的Newmark-β 方法，進行求解，具有二階精度。

目前這一探索性研究已應用于工業(yè)機器人機電系統(tǒng)的動力學模型構建，與伺服控制實際應用具有吻合性。這一柔性動力學建模方法在控制領域的意義在于，可將這一方法應用于高速高精度應用場景的機器人軌跡控制，特別是要求低振動的平穩(wěn)軌跡應用，例如切割、涂膠等，這在實際工程中是常見的。

3   結論

本文通過建立了工業(yè)機器人剛性動力學模型，作為動力學前饋控制基礎，用于提升機器人控制的精度和響應，并分析了該模型忽略關節(jié)非線性特性帶來的潛在問題。針對剛性動力學模型潛在問題，考慮關節(jié)柔性因素，推導出關節(jié)柔性動力學模型，此模型更接近機器人真實固有特性，可實現(xiàn)機器人更高精度和更高帶寬的動態(tài)控制，降低末端抖動并提高系統(tǒng)穩(wěn)定性。通過Kane 方法推導建立數(shù)學模型，論證了其可行性，為類似機電系統(tǒng)建模提供指導。

參考文獻：

[1] 浙江大學.一種工業(yè)機器人時間最優(yōu)控制軌跡的優(yōu)化方法:CN202110499901.X[P].2021-08-24.

[2] 江蘇集萃復合材料裝備研究所有限公司.一種基于動力學模型的骨科手術機器人控制方法:CN202110318897.2[P].2021-06-18.

[3] 陳柏,謝本華,丁力,等.一種帶負載工業(yè)機器人動力學模型辨識方法[J]. 南京航空航天大學學報,2016,48(6):835-840.

[4] 陳永剛,樊開夫,譚晶晶,等.工業(yè)六軸機器人末端抖動的研究[J].實驗室研究與探索,2019,38(12):44-47.

[5] 張鐵,張愛民,覃彬彬,等.柔體動力學模型的機器人柔性力矩前饋控制[J].哈爾濱工程大學學報,2019,40(8):1509-1516.

[6] 哈爾濱工業(yè)大學.一種基于動力學的噴涂機器人時間最優(yōu)軌跡規(guī)劃方法:CN202110482412.3[P].2021-07-09.

[7] 康榮杰,劉躍,耿仕能,等.絲驅動連續(xù)型機器人的建模與避障控制[J]. 天津大學學報,2021,54(6):651-660.

（本文來源于《電子產(chǎn)品世界》雜志2022年3月期）