基于CS-AGA-BP神經網絡的房價預測分析
摘要:經過MATLAB編程對GA-BP神經網絡、PSO-BP神經網絡、RBF神經網絡與傳統BP神經網絡進行精度對比;另外經過計算發現CS-AGA-BP神經網絡預測精度得到提升,多次運行均方差要低于GA-BP神經網絡,可以認為模型優化取得良好的效果。
1 算法基本原理
1.1 BP神經網絡簡介
BP(back propagation)神經網絡是一種多層前饋型神經網絡,其具有三層及三層以上的多層結構,每層均由若干神經元組成,相鄰層間的神經元均實現全連接,而上下層各神經元間無連接。BP 神經網絡分為輸入層、隱含層和輸出層,輸入層和輸出層均為一層結構,節點數目分別為自變量與因變量的數目,隱含層數不設限制,依據Kolrnogorov 定理,所有3 層的BP 神經網絡均可以趨近于任意的非線性函數,因此隱含層一般取1 層,節點數目由經驗函數確定。BP 神經網絡按有導師的學習方式進行訓練,當一對學習模式提供給網絡后,網絡神經元將按“輸入層- 隱含層- 輸出層”路徑傳播,輸出層輸出網絡響應,信號誤差沿“輸出層- 隱含層-輸入層”路徑傳播以逐層修正各連接權和閾值,此過程被稱為“誤差逆傳播算法”,隨著修正次數的增加,網絡對輸入模式響應的正確率不斷提高,輸出值逐步逼近期望輸出。BP 神經網絡示意圖如圖1 所示。
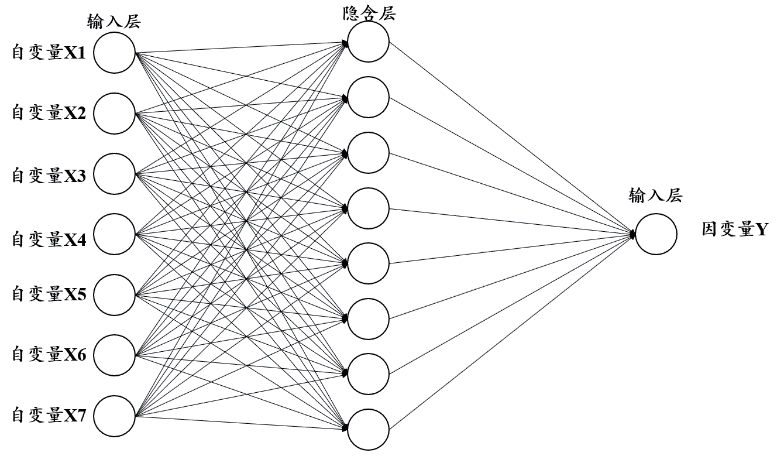
圖1 BP神經網絡模型結構
有監督的BP 神經網絡機器學習步驟:BP 神經網絡共有輸入層、隱含層和輸出層3 層結構,設輸入層有m個變量,隱含層有l 個變量,輸出層有n 個變量。輸入層、隱含層和輸出層的節點分別用下標g、h、j 表示;用ω gh 表示輸入層和隱含層節點間的權值,用ah 表示閾值;用ω hi 表示隱含層和輸出層節點間的權值,用bi 表示偏置;學習速率設置為θ 。對于輸入的因變量數據x,設其目標輸出值為y* ,實際輸出值為y 。將選定的數據組作為樣本進行網絡訓練,根據目標輸出值與實際輸出值間的誤差進行正、反向傳遞處理。
計算正向反饋:當輸入第j 個數據時,由輸入層節點g 到隱含層節點h 的總輸入(加權和)為:
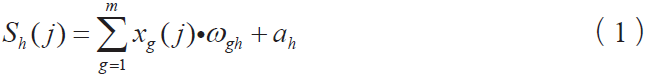
輸入值和隱含層之間的關系通過激勵函數——Sigmoid 函數處理,隱含層節點h 的輸出值為:
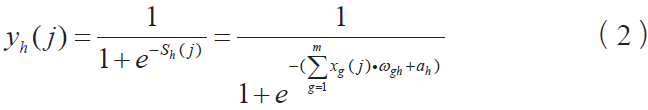
則輸出層節點i 的輸出值為:

因為Sigmoid 激勵函數連續可微,所以訓練指標函數也連續可微。
反向傳遞調整各層權值:為使誤差盡量減小,進行網絡訓練時需要逐步對網絡結構進行優化,采用梯度下降法對權值 ωgh 、ωhi 和閾值ah 、bi 進行更新以優化網絡結構。
多次對權值和閾值進行修正后網絡達到預先設定的目標誤差或者最大學習次數則結束算法,網絡訓練成功。
1.2 遺傳算法簡介
遺傳算法(genetic algorithms,GA)是一種基于達爾文進化論中的自然選擇原理和自然遺傳機制的搜索(尋優)算法,其通過模擬自然界中的生命進化機制在人工系統中的特定目標進行逐步優化。遺傳算法實質類似于粒子群算法和模擬退火等智能算法,屬于群體搜索技術,其中的種群會依據適者生存的原則逐代進化,最終得到最優解或準最優解。其必備步驟包含以下幾種:初始群體的產生、計算群體中個體的適應度、依據適者生存的原則選擇適應度較大的優良個體、被選出的優良個體兩兩配對,隨機交叉染色體基因并隨機變異某些基因生成新群體,按此方法逐代進化,直至達到迭代次數或滿足精度時終止進化,找出最優解。
生物中的遺傳概念在遺傳算法中的對應關系如表1所示。
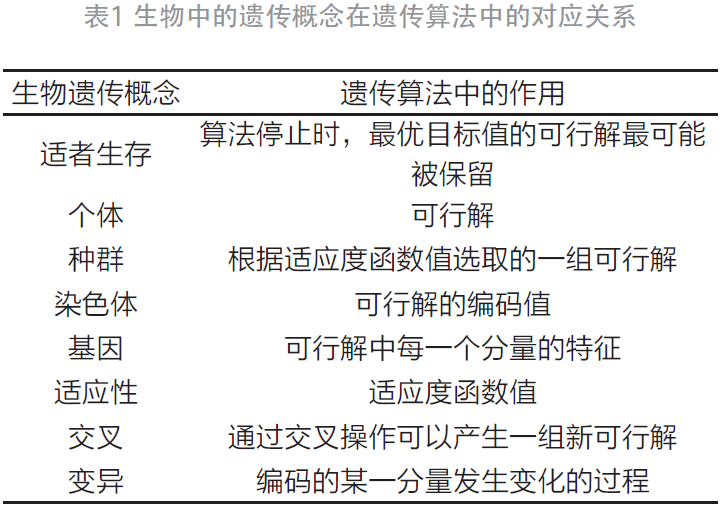
1.3 GA-BP神經網絡簡介
傳統BP 神經網絡存在收斂速度慢且不利于尋求全局最優解的缺點,而利用遺傳算法對原始BP 神經網絡進行優化可以對BP 神經網絡的權值和閾值進行更加精確的修正與優化,遺傳算法的加入可以有效克服BP 神經網絡容易陷入局部最優且收斂速度慢的缺陷。遺傳算法部分參數需要根據經驗進行設定,本研究涉及的遺傳算法參數如下。
進化終止代數:進化終止代數即最大迭代次數,進化終止代數過小可能不會得到收斂的結果,過大則會造成過擬合現象。本研究選取最大迭代次數為20。種群規模:種群規模過小會造成病態基因的出現概率增大,不利于種群的進化,過大則會造成難以收斂且會浪費資源。本研究選取種群規模為10。交叉概率:交叉概率關系到種群的更新速率,過大會破壞已有的較好的種群,捕捉不到最優解,過小則不能有效更新種群。本文選取交叉概率為20%,后續采用自適應更新公式自行確定交叉概率。變異概率:變異概率關系到種群的多樣性變化,變異概率過小會造成種群多樣性下降過快,部分缺陷基因迅速丟失且不易修補,過大則會造成高階模式的破壞概率增大。本研究選取變異概率為10%,后續采用自適應更新公式自行確定變異概率。利用遺傳算法對BP 神經網絡進行優化的具體流程如下。
1)遺傳算法參數初始化:對遺傳算法中的迭代次數、種群規模、交叉概率和變異概率進行初始化,迭代次數取20,種群規模取10,交叉概率取20%,變異概率取10%。
2)種群初始化:將種群的信息定義為一個結構體,存儲10 個個體的適應度值和染色體的編碼信息。
3)染色體編碼和適應度計算:遍歷10 個種群的循環,通過對各種群中每個個體的染色體隨機賦值并測試其取值是否位于變量邊界限制內,只保留符合條件的編碼;將編碼后的染色體分段,分為輸入層與隱含層連接的權值、隱含層神經元閾值、隱含層與輸出層連接的權值和輸出層神經元閾值,將編碼作為神經網絡權值的賦值,設置網絡的進化參數,迭代次數為20,學習率為10%,最小目標值誤差為0.000 1,訓練網絡并進行模擬預測,將預測值與實際值之差的絕對值作為染色體對應的適應度值。
4)確定最優染色體:根據適應度值挑選出最好的染色體適應度。
5)優良個體的選擇:將個體適應度值取倒數得到的數值作為其被選中的可能,將所有個體的可能值歸一化處理作為概率,該值越大說明適應度值越小,該個體越優良,越容易作為父代經歷交叉變異的過程,采用輪盤賭算法隨機產生選擇值,根據其落在哪個個體的概率區間內,將該個體作為父代并儲存信息。輪盤賭規則的算法流程和轉盤概率分布示意如圖2 所示。
6)交叉和變異:對種群所有個體進行遍歷,依據交叉概率隨機選取2 條染色體并隨機選擇交叉位進行交叉,如果2 條染色體均可行則進行交叉,然后對新的種群信息進行存儲;依據變異概率隨機選取2 條染色體并進行變異,如果2 條染色體均可行則進行變異,然后對新的種群信息進行存儲。
7)最優初始閾值和權值的賦值:將進化了20 代的種群的最優的基因賦值給神經網絡用來預測。
8)神經網絡的訓練與測試:得到最優權值和閾值以及輸入層、隱含層和輸出層的數值后,利用訓練數據對網絡進行訓練,然后利用后面較少的數據進行預測以及誤差檢驗。
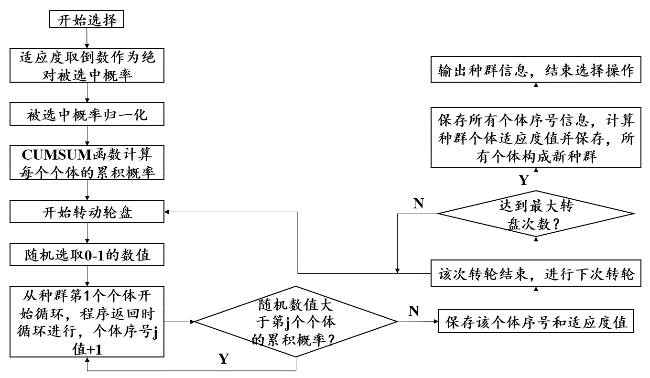

圖2 輪盤賭規則的算法流程和轉盤概率分布示意圖
1.4 CS-AGA-BP神經網絡的改進簡介
為更大程度地增強BP 神經網絡的優化效果,本文最終采用CS-AGA-BP 神經網絡對原模型進行改進。改進分為兩個方向:①交叉概率和變異概率采用自適應算法確定;②通過Logistic 混沌序列對交叉位置進行確定,并進行多基因變異。
普通遺傳算法中的交叉率和變異率是人為給定的,其對遺傳算法的行為和性能有著關鍵影響。交叉率過大,新個體產生的速度就越快,但是很容易破壞遺傳模式,一些高適應度的個體結果很快就會被破壞,如果交叉率過小,個體間不能傳遞信息產生新個體,搜索過程會變得緩慢甚至停滯不前;變異率過大,遺傳算法就變成了隨機搜索算法,變異率過小就不易產生新個體。基于此,Srinvivas 等人提出用自適應遺傳算法來控制交叉率和變異率的大小,使其隨適應度自動改變,適應度越接近最大適應度值,交叉率和變異率就越小,為防止進化初期最優個體不發生交叉和變異,對其交叉率和變異率進行初始化,同時為了防止每一代的最優個體被破壞,通過精英選擇策略將它們直接復制到下一代。交叉率和變異率的調整公式為:
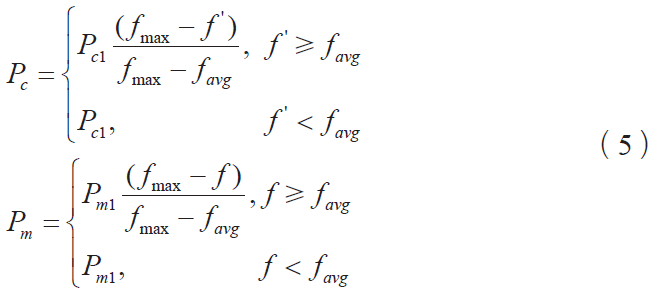
其中, fmax 為全體中最大的適應度值, favg 為全體的平均適應度值, f ′ 為交叉的2 個個體中較大的適應度值, f為變異個體的適應度值。該式中Pc1 取值為0.2, Pm1 取值為0.1。
遺傳算法跳出局部最優解尋求全局最優解時依賴于交叉和變異操作,在交叉操作中,單點交叉(段交叉)、多點交叉和均勻交叉使用較多;變異操作一般使用Guassian 分布的隨機變異來實現。許多學者采用不同方法進行變異操作以優化遺傳算法,但改進效果并不明顯。而混沌系統可以對交叉和變異操作同時進行改進,在交叉操作中,以“門當戶對”原則進行個體配對,通過混沌序列確定交叉點,確保算法收斂精度,削弱和避免尋優抖振問題;在變異操作中,混沌序列可以對染色體中多個基因進行變異,以避免算法早熟。本文采用Logistic 混沌序列進行遺傳改進,如式所示:
x(n +1) = 4x(n)[1? x(n)] (6)
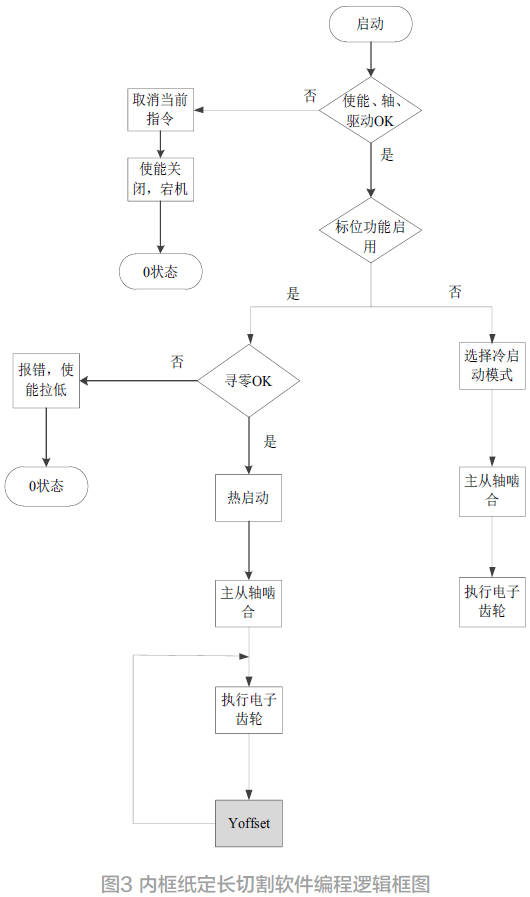
CS-AGA-BP 神經網絡優化過程如圖3 所示。
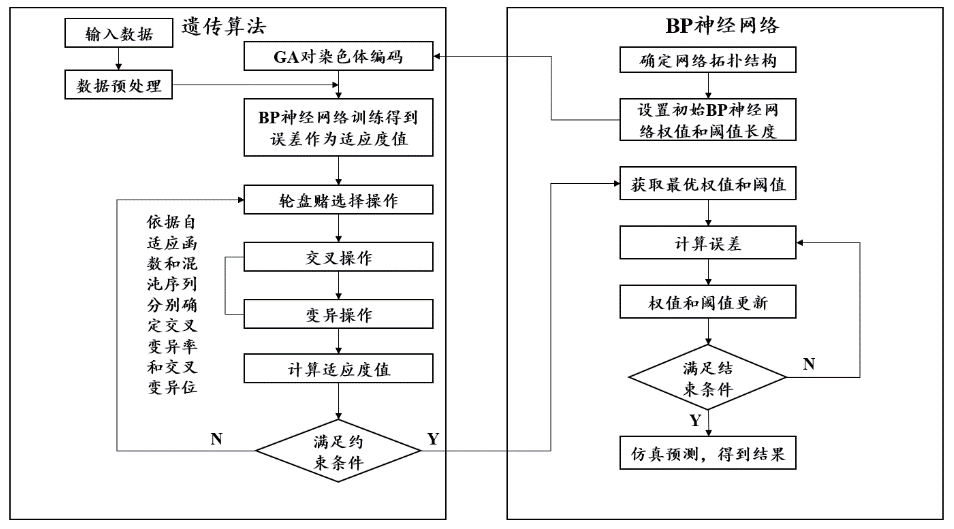
圖3 CS-AGA-BP神經網絡流程設計
2 算法的基本算例
2.1 數據來源與處理
本文采用數據是數據挖掘領域常用的美國波士頓房價數據集,格式為506?14,取前 500 行數據,前80% 行用作訓練數據,后20% 行用作測試數據。以前13 個指標作為模型自變量,以MEDV 作為模型因變量。
為便于將輸入樣本矩陣的輸入范圍控制在(-1,1)內以消除量綱影響,需運用MATLAB 軟件中的mapminmax 函數對所有數據進行歸一化處理,即:
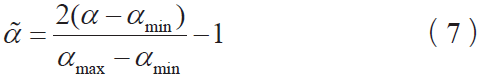
其中, α 是歸一化前的變量; αmax 和αmin分別為α 的最大值和最小值;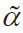 是歸一化后的變量。
是歸一化后的變量。
2.2 隱含層節點確定
神經網絡隱含層節點數的選擇相當重要,其對神經網絡的性能影響很大,如果隱含層節點數過少,神經網絡很難建立復雜的判斷界,達不到合適的訓練精度,容錯性差;隱含層節點數過多,雖然會降低誤差,提高精度,但是神經網絡會趨向于復雜,從而造成訓練時間增加和過擬合的情況。為確保在滿足精度的前提下降低網絡復雜性,即選取合適的隱含層節點數目,本研究采取以下經驗函數來確定BP 神經網絡隱含層的節點數目:
![]()
其中, hiddennum 是隱含層節點的數目, inputnum 是輸入層節點的數目,outputnum 是輸入層節點的數目,α是1~10 之間的取整調節常數。本研究中inputnum =13 ,outputnum = 1 , hiddennum 取值范圍為5~14。為了挑選出最優的隱含層節點數,此處采用均方差誤差(RMSE)進行衡量,其計算公式如下所示:
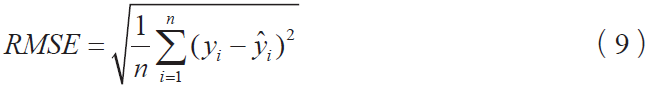
其中,n 表示樣本數目, yi 表示實際房價, y?i 表示預測的房價。
將hiddennum 從5~14 共10 個值分別代入MATLAB程序中獨立運行,最后選取RMSE 最小時的10 作為隱含層節點數。
2.3 訓練函數的選取
本文運用MATLAB 中newff 函數構建前饋型神經網絡,newff 函數中的訓練方法有基本梯度下降法(traingd)、帶有動量項的梯度下降法(traingdm)和帶有動量項的自適應學習算法(traingdx)等。本研究選取適用于遺傳算法優化神經網絡的訓練函數train 進行訓練。網絡進化參數分別設置最大迭代次數為100,學習率為0.1,最小目標值誤差為0.000 1。
3 算例的MATLAB計算結果與解析
為了便于探究GA-BP 神經網絡的優化效果,本文選取PSO-BP、傳統BP 和RBF 神經網絡與GA-BP 神經網絡的預測效果進行對比。神經網絡的學習率為0.1,迭代次數為100,隱含層節點數為10。針對后100 組數據進行預測,并將預測數據與實際數據進行對比分析誤差,如圖4 所示。
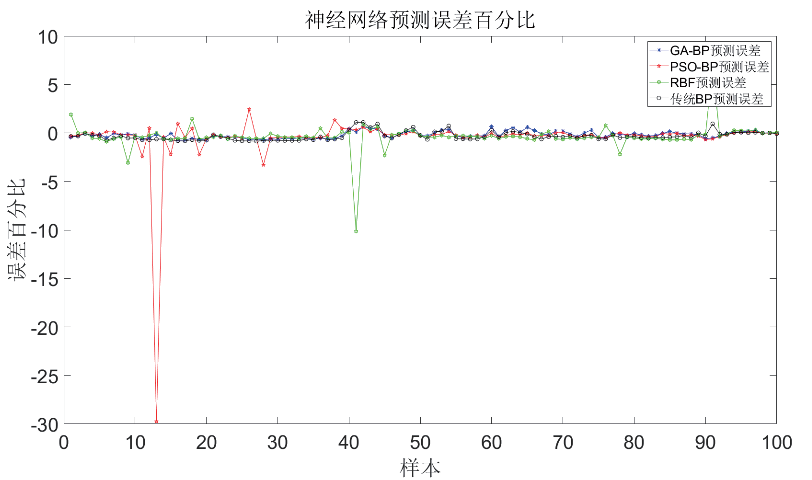
圖4 四種神經網絡預測的誤差
通過MATLAB 計算可以看出GA-BP 神經網絡和PSO-BP 神經網絡預測精度較高,但是經多次運算發現PSO-BP 神經網絡預測精度并不穩定。RBF 神經網絡和傳統神經網絡誤差較大,但是RBF 神經網絡的優點是輸出結果非常穩定。
通過CS-AGA-BP 神經網絡對數據進行訓練與預測,與原始GA-BP 神經網絡誤差百分比進行對比,如圖5 所示。
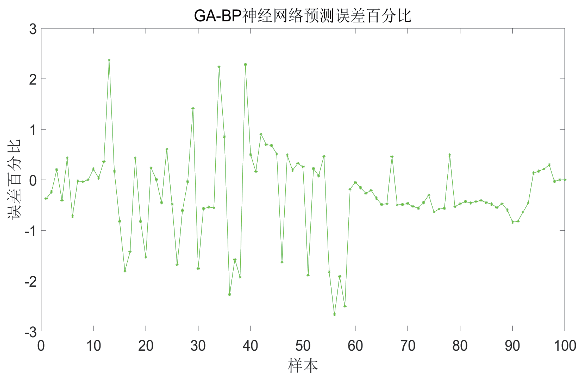
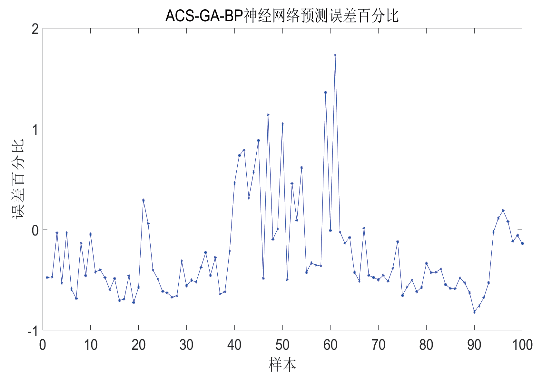
圖5 GA-BP神經網絡和ACS-GA-BP神經網絡的誤差百分比
經過MATLAB 此次計算,精度提升14.97%,雖然遺傳算法對神經網絡權值和閾值的更新具有隨機選擇性,但經過多次計算對比取平均數,CS-AGA-BP 神經網絡的均方差要低于GA-BP 神經網絡的均方差,誤差百分比也有所減小,因此可以認為模型優化取得良好的效果。
參考文獻:
[1] GEN?AY R,YANG X.A forecast comparison of residential housing prices by parametric versus semiparametric conditional mean estimators[J].Economics Letters,1996,52(2):129-135.
[2] 王宇星,黃俊,潘英杰.GA-BP神經網絡在老人負性情緒預測中的應用[J].小型微型計算機系統,2020,41(8):1702-1706.
[3] 羅博煒,洪智勇,王勁屹.多元線性回歸統計模型在房價預測中的應用[J].計算機時代,2020(6):51-54.
[4] 楊再宋,謝菊芳,胡東,等.基于AW-GA-BP算法的配電網設備運行環境相對濕度的預測方法及應用[J].重慶師范大學學報(自然科學版),2019,36(6):104-109,2.
[5] 惠天宇,杜尚勉,陳樂至,等.基于GA-BP神經網絡的手足口病疫情預測[J].教育教學論壇,2020(38):133-134.
[6] 魯明.基于PCA-GA-BP模型對污水BOD的預測[J].湖北汽車工業學院學報,2019,33(4):57-61,76.
[7] 羅成.基于SVD-GA-BP神經網絡模型的股價預測[J].佳木斯大學學報(自然科學版),2019,37(6):988-991.
[8] 趙銘生,劉守強,紀潤清,等.基于遺傳算法優化BP神經網絡的華北型煤田礦壓破壞帶深度預測[J].礦業研究與開發,2020,40(6):89-93.
[9] 司守奎,孫兆亮.數學建模算法與應用[M].北京:國防工業出版社,2015.
[10] 閔江濤,楊杰,馬晨原.基于改進GA-BP網絡算法的邊坡力學參數反演分析[J].水電能源科學,2019,37(11):152-155.
[11] NING M,GUAN J,LIU P,et al.GA-BP air quality e v a l u a t i o n m e t h o d b a s e d o n f u z z y t h e o r y [ J ] .Computers,materials & continua,2019,58(1):215-227.
[ 1 2 ] TANG T , Y u a n S, T a n g Y, e t a l .Op t i m i z a t i o n o f impulse water turbine based on GA-BP neural network a r i t h m e t i c [ J ] . J o u r n a l o f m e c h a n i c a l s c i e n c e a n d technology,2019,33(1):241-253.
(本文來源于《電子產品世界》雜志2021年12月期)



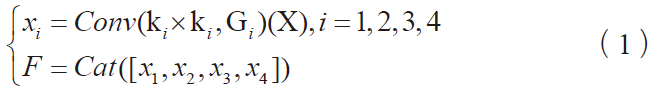
評論