摘要：針對采用常規控制方式的PWM整流器存在動靜態性能較差的問題，提出了一種PWM整流器的新型控制方法。該方法電壓外環采用滑模控制，電流內環采用內模控制，結合了滑模控制和內模控制的優點，即充分利用滑模控制的魯棒性強、對負載的擾動具有很好適應性的優點，以及內模控制的良好跟蹤性能和較高的穩態精度，使系統具有良好的動靜態性能。以基于LCL濾波的三相電壓型PWM整流器為研究對象，對其電流內環和電壓外環進行了設計與分析，仿真和實驗結果證明了所提方法的有效性和優越性。
關鍵詞：整流器；濾波器；內模控制；滑模控制

1 引言
電壓型PWM整流器具有網側電流為正弦、網側功率因數可控、電能雙向傳輸、動態性能較快等優點，因此在有源電力濾波、統一潮流控制器、超導磁能儲能等很多領域均有廣泛應用。
PWM整流器最常用的控制方式是基于電網電壓矢量定向的PI控制。為了得到良好的動態性能和解耦控制，需引入前饋補償項，影響了控制系統的魯棒性。由于內模控制具有良好的跟蹤性能和較高的穩態精度，在靜止坐標系下不存在耦合項和前饋補償項；滑模控制具有魯棒性強、對負載擾動有很好的適應性的優點，因此這里提出了一種新的PWM整流器控制策略，即電流內環采用內模控制，電壓外環采用滑模控制，使系統同時具有滑模控制和內模控制的優點。

2 三相電壓型PWM整流的數學模型
基于LCL濾波的三相PWM整流器的拓撲結構如圖1所示。

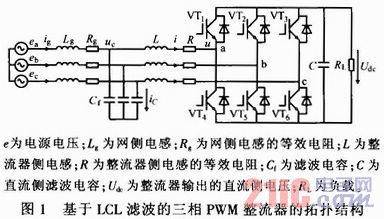
低頻時，忽略濾波電容的作用，將網側電感和交流側電感用一個等效電感來代替。三相電壓型PWM整流器在兩相靜止坐標系下的數學模型為：

對式(1)進行兩相靜止到兩相旋轉坐標變換，可得d，q坐標系下的數學模型為：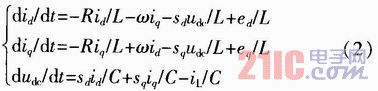


3 控制系統設計
3．1 電流內環的設計
由式(1)的數學模型變形得到：

基于內模控制PWM整流器的電流環控制結構框圖如圖2所示，如果內模控制器增加一個比例增益，系統的動態性能會變得更好。

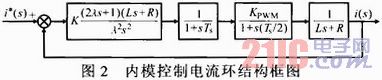
當λ=0．008時，畫出電流內環的根軌跡，按二階最優原理，使系統的阻尼系數為0．707，可知比例增益K=8．34，再畫出系統的波特圖，由圖可知系統的相角裕度γ=63．6°，截止頻率fc=242 Hz，滿足fn≤fc≤10fn，控制器符合設計要求，系統穩定。
3．2 電壓外環的設計
為了提高電壓型PWM整流器直流側電壓的動態響應和魯棒性，采用滑模變結構控制設計電壓環。三相電壓型PWM整流器在d，q坐標系下
的數學模型為式(2)，將其改寫為狀態方程：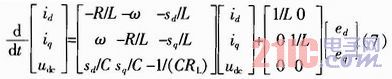

由式(7)可知，PWM整流器有sd，sq兩個控制量，其中sd用來控制PWM整流器直流側電壓udc，sq用來控制無功電流iq以獲得期望的功率因數。對于式(7)期望輸入正弦電流，且功率因數為1，輸出電壓為設定值，故可選取udc和iq為系統輸出，則式(7)改寫為：

根據式(12)來設計滑模控制器。

4 仿真和實驗結果
4．1 仿真驗證
在Matlab／Simulink中建立仿真模型，控制結構如圖3所示，采用傳統的雙閉環結構，電壓外環采用滑模控制，電流內環采用內模控制，仿真參數：電源電壓有效值為60 V，直流側電壓為150 V，開關頻率為5 kHz，直流側濾波電容值為3 000μF，負載為30 Ω，系統的阻尼電阻為8Ω。

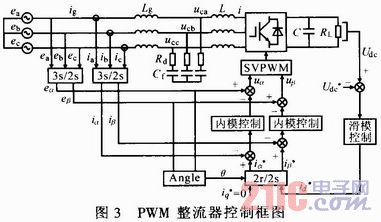
由整流器電網側電壓和電流仿真波形及電流頻譜分析可知，電壓電流工作在單位功率因數，且網側電流畸變很小。由整流器直流側電壓仿真波形可知，外環采用滑模控制，內環采用內模控制的控制方法比雙環都采用內模控制時的調節時間更短，動態響應快。

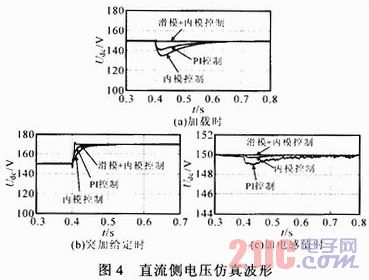
圖4a為突加負載時直流側電壓波形，圖4b為突加電壓給定時直流側電壓波形，由圖可知，外環采用滑模控制，內環采用內模控制的魯棒性最強，PI控制次之，內模控制的魯棒性最差。圖4c為突加濾波電感時直流側電壓波形，由圖可知，外環采用滑模控制，內環采用內模控制對被控對象的數學模型精度要求最低，內模控制次之，PI控制對被控對象的數學模型精度要求最高，由此說明外環采用滑模控制，內環采用內模控制的控制方法可將兩種控制方法的優點結合在一起，有更好的控制效果。
4．2 實驗結果
為了進一步驗證以上控制方法的正確性，搭建了以TMS320F2812為控制核心的三相電壓源型PWM整流器的實驗平臺。系統參數與仿真一致，所得到的波形如圖5所示。圖5a為穩態時整流器網側a相電壓和電流實驗波形，由圖可見，整流器的網側電壓與電流幾乎是同相位的，且正弦度很好，功率因數接近于1。圖5b為突加負載時整流器直流側電壓波形，由圖可見，系統的魯棒性很強，達到了控制目的。

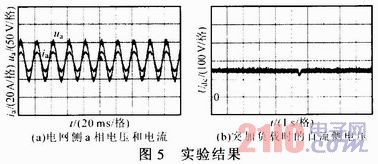
通過仿真和實驗，證明了外環采用滑模控制，內環采用內模控制的雙閉環控制系統可以充分結合兩者的優點，具有優異的動靜態性能。

5 結論
這里提出了一種PWM整流器控制策略，即電壓外環采用滑膜控制，電流內環采用內模控制，使系統不僅具有滑模控制對負載擾動和系統參數漂移的良好適應性以及良好的快速性，而且具有內模控制對被控對象參數依耐性小、能獲得良好跟蹤性能和較高穩態精度的優點，因此系統具有優異的動靜態性能。仿真分析和實驗表明了所提出方法的有效性和優越性。