第一章 緒論

1.1 引言

計算機斷層攝像技術CT(Computerized Tomography)是20世紀醫學的重大成果之一，該成果將計算機應用于醫學領域，使醫學射線學發生了革命性的變化。自從CT問世以來，計算機科學與生物醫學工程相結合，形成了計算機醫學圖像研究的新領域，并為生命科學的研究提供了新的方法，成為近年來世界科技界最活躍、最富有生機和成就的領域之一。

醫學影像學將數字圖像處理技術和計算機圖形學技術廣泛的應用于生物醫學領域中，通過把人體的內部結構以圖像或圖形的方式顯示出來，提高了醫療診斷的可靠性，使治療能夠準確和徹底。

1.2 醫用CT的簡介

CT是計算機X射線斷層造影術(Computerized Tomography)的簡寫。CT的發明是20世紀后期最重大的科技成果之一，由Hounsfield于1969年設計成功，1972年公諸于世。

CT利用人體各種組織(包括正常和異常組織)對X射線的吸收不等這一特性，將人體某一選定層面分成許多立方體小塊(這些立方體小塊稱為體素)，X射線通過人體測得每一體素的密度或灰度，即為CT圖像上的基本單位，稱為像素。它們排列成行列方陣，形成圖像矩陣。當X射線球管從一方向發出X射束穿過選定層面時，沿該方向排列的各體素均在一定程度上吸收一部分X射線，使X射線衰減。當該X射線束穿透組織層面(包括許多體素)為對面探測器接收時X射線量已衰減很多，為該方向所有體素X射線衰減值的總和。然后X射線球管轉動一定角度，再沿另一方向發出X射線束，則在其對面的探測器可測得沿第2次照射方向所有體素X射線衰減值的總和;以同樣方法反復多次在不同方向對組織的選定層面進行X射線掃描，即可得到若干個X射線衰減值總和。在上述過程中，每掃描一次，即可得一方程。該方程中X射線衰減總量為已知值，而形成該總量的各體素X射線衰減值是未知值。經過若干次掃描，即可得一聯立方程組，經過計算機運算可解出這一聯立方程組，而求出每一體素的X射衰減值，再經模/數轉換，使各體素不同的衰減值形成相應各像素的不同灰度，各像素所形成的矩陣圖像即為該層面不同密度組織的灰度圖像。

螺旋CT檢查包括兩方面的基本內容：一是X射管及探測器連續360°旋轉;二是患者同時隨檢查床勻速推進，如圖1.2所示。在掃描時間內，X射線焦點對病人作螺旋式運動，并同時收集這一范圍的全部掃描數據，用線性內插法重建圖像。

如圖1.3所示，醫用X-CT機的系統結構主要由六大部分組成，其各部分的作用如下：

(1)X射線源：產生用來檢測被測物的X射線，X射線源包括X射線球管源(能量在450kV以下)和直線加速器(能量在2MeV以上)。射線源的能量，決定了穿透能力。

(2)探測系統：包括準直器、傳感器、信號處理和信號傳輸等部分，是獲取信號的關鍵部分，也是決定CT性能的關鍵部分之一。穿過被測物的X射線首先通過準直器準直并離散化，傳感器先將射線轉換成電信號，信號處理電路再將不規則的信號轉換成標準的信號傳輸到計算機接口。

(3)計算機采集系統：主要由特殊的專用的多信道數據采集接口電路和計算機軟硬件組成。完成數據采集、轉換、校正、處理等。將采集的數據處理成標準的文件格式，供圖像重建、處理使用。

(4)機械掃描系統：作為各部分的載體并提供CT掃描所需的多個自由度的高精度運動。

(5)自動控制系統：包括檢測、驅動、控制器(計算機)，完成掃描運動控制、系統邏輯和程控、狀態監控和安全保護，協調整機工作，并完成系統自檢與數據診斷。

(6)圖像處理系統：包括圖像處理計算機硬件和軟件，如用于圖像重建與處理的高速計算機、大屏幕圖像顯示器、大容量數據存貯器、圖像拷貝輸出設備(打印機)、系統軟件及專用軟件。完成數據校正、圖像重建、處理、分析、測量、圖像輸出、存貯、顯示等。

我們所研究的CT圖像重建部分處于圖像處理系統中，是整個系統的瓶頸所在，也是決定系統整個過程所消耗時間的關鍵部分。

1.3 CT圖像重建技術概述

1.3.1 CT圖像重建的簡介

我們試圖重建的物體可被看作是某種函數的二維分布。對于CT，該函數代表物體線性衰減系數。關于斷層重建問題的描述，我們可以假設采集了一組測量結果，每個測量結果代表沿著特定的射線路徑，物體衰減系數的累加或線積分。這些測量結果是在不同角度和到旋轉中心的不同距離上獲取的。為避免數據采樣的冗余，我們假設測量按以下次序進行。首先沿著彼此平行且等間距的路徑進行一組測量。這些測量結果構成一次“觀測”或一組“投影”。在略微改變的角度下重復同樣的測量。持續該過程直到覆蓋整個360°(理論上僅有180°平行投影是必要的)。在整個過程中，相鄰兩次觀測之間的角度增量保持不變，并且被掃描物體在同一位置固定不動。CT重建的問題就是，我們如何基于這些測量結果來估計被掃描物體的衰減系數分布。

CT圖像重建問題是一個有趣而復雜的課題。它的公示表達可以追溯到1917年，當時Radon(雷登)[2]首先找到了從函數線積分重建該函數的求解方法。隨著20世紀70年代后期和80年代早期臨床實用CT掃描機的發展，該領域的研究活動有了極大的發展。大量研究論文、會議論文匯編、書籍章節，甚至教科書都關注這個課題[3,4]。提出了許多技術，它們在計算復雜性、空間分辨率、時間分辨率、噪聲、臨床治療方案、靈活性以及偽像各方面具有不同的折中平衡。

1.3.2 Radon(雷登)變換

CT的基本思想源于1917年奧地利數學家Radon提出的Radon變換。

Radon變換的內容可以表述為：若已知某函數，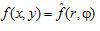

如圖1.4所示，其沿直線S的線積分為：

(1.1)

則

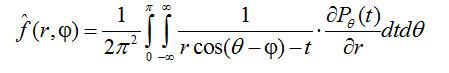
(1.2)

式(1.1)為Radon變換，實際上就是物體的投影，式(1.2)為Radon反變換，即根據投影數據 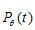重建函數 。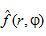

1.3.3 傅里葉切片定理

傅里葉切片定理的含義是：平行投影的一維傅里葉變換等同于原始物體的二維傅里葉變換的一個切片。即是指出線性衰減系數函數f(x,y)在某一方向上的投影函數gθ(R)的一維傅立葉變換函數Gθ(ρ)是f(x,y)的二維傅立葉變換函數F(u,v)或F(ρ,θ)(極坐標形式)在(ρ,θ)平面上沿同一方向且過原點的直線上的值，如圖1.5所示。

為此，我們在不同的角度下取得足夠多的投影函數數據，并作它們的傅立葉變換，那么變換后的數據就將充滿整個(u,v)平面。一旦頻域函數F(u,v)或F(ρ,θ)的全部值得到后，將其作一次傅立葉反變換，就得到原始的衰減系數函數f(x,y),即

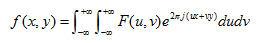
(1.3)

令u=ρcosθ，v=ρsinθ，則式(1)可進一步變形為

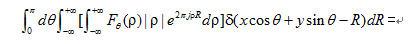
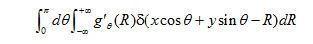
(1.4)

式中 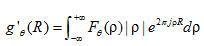，表示對投影函數 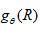的傅里葉變換函數進行濾波變換，其中 為濾波函數。

由傅立葉變換性質可知，頻域中的濾波運算可等效地在空域中用卷積運算來完成，因此由(2)可得到

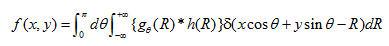
(1.5)

式中h(R)為濾波函數 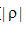的空域形式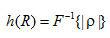， ，因而這種方法也稱為卷積反投影方法。

利用中心切片定理[5]及二維FFT反變換法重建圖像，由于勿須反投影運算,因而速度快,但圖像重建過程中,需要內插運算，因而重建圖像精度相對較低。

首先求出各投影數據的一維傅里葉變換，在不同的投影角度下所到的一維變換函數可構成完整的二維傅里葉變換函數，將此二維函數作一次反傅里葉變換，就得到重建圖像。為了在二維逆變換中采用快速傅里葉變換算法，通常在逆變換前要將極坐標轉化為直角坐標的形式。

傅里葉變換法重建法的特點是變換速度快，但精度不如濾波反投影法。算法的關鍵是將弧形的的極坐標數據轉換成直角坐標數據時，由于在邊緣區高頻數據減少，因而造成誤差，但傅里葉變換重建法重建速度比濾波反投影可提高2-3倍一在弧形極坐標數據向直角坐標系轉化時，最簡單的是最鄰近內插法，當然這種方法精度最低，雙線性內插重建圖像精度好于最鄰近內插法，而且計算又不復雜。

解決的方法是擴大計算區域，通過外延數據附加上一些格外的點，即計算更多的像素點以減小邊緣的誤差。如重建圖像為M×M，則可計算3M×3M區域內的FFT變換，當然這是以增加了計算量為代價的。傅里葉變換重建圖像算法在內插網格點上進行一些適當的選擇。如使徑向點取在直角坐標網格的線上，這樣只需一次內插，而重建圖像精度有了較大的改進。

1.3.4 CT圖像重建的幾種算法

在實際重建當中所存在的問題是，雖然Radon給出了一個數學公式，但是我們需要一個有效的算法來解決它，圖像重建的算法有很多，大致分為三類：精確算法、近似算法和迭代算法。近似算法中，以濾波反投影算法(Filter back projection，FBP)最具代表性，應用最為廣泛。選代算法中，代數重建算法(Algebraic reconstruction technique，ART)是提出最早并最為人們熟悉的算法。迭代型算法(如代數重建算法等)具有許多優點，但由于計算量大、重建時間長.在很長一段時間內限制了其在醫學和工業CT領域的應用。提高迭代型算法的計算速度一直是人們關注的問題。近年來人們提出了不少提高迭代算計算速度的方法，加上近年來計算機計算速度的迅速提高，迭代算法重新受到人們青睞。此外，由于應用的需要，局部重建算法(Local Reconstruction Algorithm， LocalRA)也在近十年中有了較大的發展。在傳統全局CT算法中，即使重建物體斷面中一個小區域的圖像，也得圍繞整個斷面采集投影數據。而局部重建算法，僅需圍繞感興趣區域及其鄰域采集投影數據，即可重建感興趣區域的圖像。局部重建算法可減少數據采集時間和重建時間，降低人體(或生物體)的放射攝入量。