基于特征選擇改進LR-Bagging算法的電力欠費風險居民客戶預測
3 應用與結果
本文引用地址:http://www.j9360.com/article/201703/345948.htm本應用以“電費回收風險”為主題,要求根據2015年8月至2015年9月貴州貴陽電網欠費居民樣本客戶的行為分析和特征擬合,以及與全量居民客戶的特征匹配,采用分群管理理論和數據挖掘算法建立數學模型,計算出全量居民客戶的電費回收風險程度,自動分析識別出欠費高風險居民客戶群。
本部分主要通過改進的LR-Bagging算法與單一逐步邏輯回歸算法在電力欠費高風險居民客戶的預測的應用效果的比較來展開。借助的分析工具為R語言。
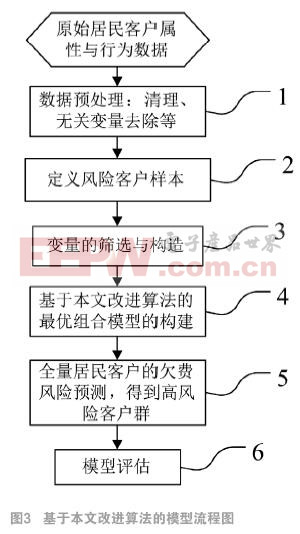
3.1 基于本文改進算法的模型流程圖
針對本應用的實際情況,結合改進算法的數據需求,整體實際操作過程的流程可以表述如圖3。
3.2 模型與結果
綜上所述,有如下處理過程:
3.2.1 定義風險客戶樣本
業務經驗告訴我們,并非所有的欠費居民客戶都是存在欠費風險的客戶,因為我們并不排除多數欠費居民客戶因為忘記繳費日期而出現欠費的可能性。一般情況下,存在欠費風險的居民客戶占全量客戶的比例不超過25%。因此,考慮通過所有欠費居民客戶在2015年8月至9月的累計欠費金額的四分之三分位點作為定義欠費風險居民客戶的標準。
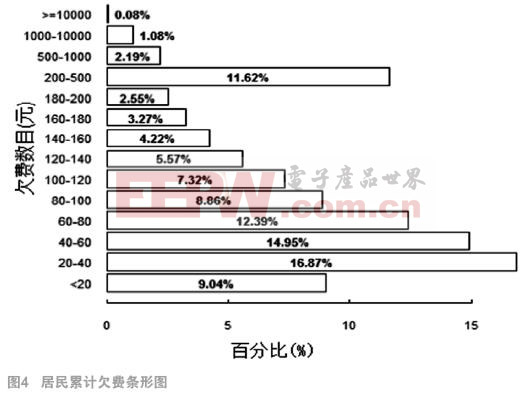
圖4為全部居民客戶在2015年8月至9月累計欠費金額的概率直方圖,可以發現,大約75%的居民客戶的累計欠費金額在140元以下。經過與電網專家的商討,認為可選定該數據為是否為欠費風險客戶的閾值。
綜上所述,我們定義“壞客戶”樣本,即欠費風險客戶樣本的標準為:在2015年8月至9月期內,累計欠費金額超過140元的居民客戶。
3.2.2 變量的構造與篩選
原始居民客戶數據包含包括年齡、用電性質、合同容量等基本屬性以及總用電量、電費實際金額等歷史行為屬性在內的25個字段,顯然,變量個數過多,需要進行篩選,具體操作為:
對于連續型變量,計算其與因變量“是否為壞客戶”的spearman相關系數,大于0.5的情況下保留;對于離散型變量,對其與因變量做卡方檢驗,保留在0.05顯著性水平下的顯著變量,最終確定的用于建模的變量為:平均用電量、平均電費、平均繳費時長、信譽分數、用電類別、行業代碼、合同容量、城鄉標志,對應地設置為X1~X8。
同時,考慮到離散變量對于邏輯回歸的效果影響,基于目標變量對WEO其做編碼處理。WEO叫做證據權重(Weight of Evidence),表示的其實是自變量取某個值的時候對欠費比例的一種影響。若WEOi表示離散變量的第i個類值的證據權重,則有:
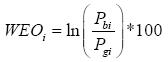 (8)
(8)
其中,Pbi和Pgi分別表示離散變量取第i個類值時,欠費風險客戶占比和非欠費風險客戶的占比。
最后,隨機抽取已完成前述處理的居民客戶樣本的10%,共條記錄作為構建模型的初始數據 。
3.3 建模
3.3.1 本文改進算法模型
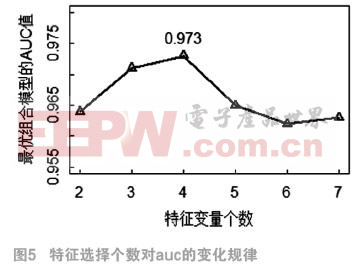
基于特征選擇改進的LR-Bagging組合模型雖然增加了分類結果的精度,但特征選擇的隨機性也不可避免的增加了模型的偶然性。顯然,每一次特征變量個數發生改變。在其他條件不變的狀態下,隨著循環次數的增加,至于特征變量的個數對模型結果的影響規律,我們甚至無法預知。對此,本處采用了實證比較的方法來初步確定上述兩影響因素的最優數值,即通過不斷改變特征變量探究模型效果的變化。模型的效果的好壞仍采用采用AUC值來衡量。即令特征變量個數k滿足: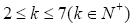 ,同時,基于經驗,我們設置訓練集與測試集的樣本比例為7:3,ε的值為0.05,則利用本文算法可以得到不同的組合模型。
,同時,基于經驗,我們設置訓練集與測試集的樣本比例為7:3,ε的值為0.05,則利用本文算法可以得到不同的組合模型。
觀察圖5不難發現,在其他條件不變的情況下,隨著特征變量個數的增加,AUC總體呈現先增長后下降的的變化趨勢,且當k取值為4時,AUC最大,因此大致可以認為4為其最佳特征個數,選取 時的組合模型為本文改進算法得到的最終模型。
3.3.2 單一逐步邏輯回歸模型
對初始數據S通過逐步篩選建立邏輯回歸模型,結果為:
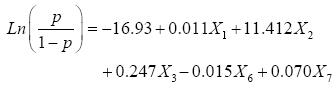
各系數均通過了0.05顯著性水平下的公式(6)的正態分布檢驗。因此,該模型是顯著有效的。
4 模型評估
分別采用本文基于特征選擇改進的LR-Bagging算法的組合模型與單一LR模型對全量居民客戶的風險概率預測,并借助預測結果對兩者的準確性與有效性做出評估。
4.1 準確性—ROC曲線
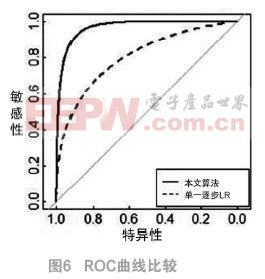
圖6表明,基于本文算法模型的預測電力欠費風險客戶的ROC曲線一直位于單一LR模型預測結果的ROC曲線上方,因此,可以認為,前者的準確性優于后者。
4.2 有效性—提升度
提升度(Lift)是評估一個預測模型是否有效的一個度量。這個比值由運用和不運用這個模型所得來的結果計算而來。一般來說提升度越大,效果明顯。
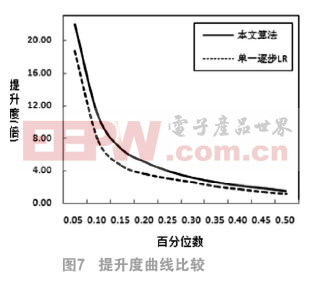
圖7表明,基于本文算法模型的預測電力欠費風險客戶的提升度曲線一直位于單一LR模型預測結果的提升度曲線上方,因此,可以認為,前者的提升度較大,有效性優于后者。
5 結論
本文從電力欠費風險預測的角度出發,提出了一種基于特征選擇改進的LR-Bagging(即以邏輯回歸為基分類器的Bagging集成學習)算法,其精髓在于每一個訓練的LR基分類器的記錄和字段均通過隨機抽樣得到。且算法的終止迭代準則由AUC統計量的變化率決定。該改進算法充分考慮了LR的強泛化能力、bagging的高精確度以及特征選擇帶來的LR基分類器的多樣性、弱化的多重共線性與“過擬合”度,效果優于單一LR模型。且最終的實驗表明,該改進算法得到的電力欠費居民客戶風險預測模型的準確定性與有效性得到提升。而下一步,可針對改進算法中最優變量個數的確定問題展開探討,或考慮將其推廣至其他應用領域。
參考文獻:
[1]顧曦華.濟南供電公司電力大客戶欠費風險預警研究[D].保定:華北電力大學,2007.
[2]田慧欣,王安娜.基于增量學習思想的改進AdaBoost建模方法[J].控制與決策,2012,27(9):1433-1436.
[3]李亞林,王茜.對電力營銷中全過程電費風險管理的探究[J].電力技術,2016,1(148):165-165.
[4]張宇獻,李松,董曉.基于特征聚類數據劃分的多神經網絡模型[J].信息與控制,2013,42(6):693-699.
[5]朱志華.電力客戶信用評價與欠費風險預警系統的總體設計[J].現代計算機(專業版).2009(01):188-190.
[6]周暉等.基于Logistic回歸模型的電力客戶欠費違約概率的預測[J]. 電網技術,2007,31(17):85-88.
[7]黃文思.基于決策樹算法的電力客戶欠費風險預測[J].電力信息與通信技術,2016,14(3):20-22.
[8]馬新宇.基于Bagging集成學習的水華預測方法研究[J].計算機應用化學,2014,31(2):140-144.
[9]Ma Ranran. Research of Ensemble Learning Algorithm. Shandong:Shandong Univerity of Science and Technology,2010.
[10]朱紹文,胡宏銀,王泉德,等.決策樹采掘技術及發展趨勢[J].計算機工程,2000,26(10):1-3.
[11]李海波,柴天佑,岳恒.浮選工藝指標KPCA-ELM軟測量模型及應用[J].化工學報,2012,63(9):2892-2898.
[12]馬冉冉.集成學習算法研究[D].濟南:山東科技大學,2010.
[13]施彥.物流中心選址的神經網絡集成模型研究[J].計算機工程,2009,45(16):211-214.
[14]劉淑蓮,王真,趙建衛.基于因子分析的上市公司信用評級應用研究[J].財經問題研究,2008,15(7):53-60.
[15]張克盡,陸開宏,朱津永,等.基于神經網絡的藻類水華預測模型研究[J].中國環境監測,2012,28(3):53-57.
本文來源于《電子產品世界》2017年第4期第70頁,歡迎您寫論文時引用,并注明出處。









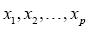
評論