功率譜、頻率分辨率、頻譜泄漏與窗函數

　　在分析和測定所采集的數據記錄時,快速傅立葉變換(FFT)和功率譜是非常有用的工具。借助這些工具能夠有效地采集時域信號、測定其頻譜成分、并對結果進行顯示。

　　功率譜圖(參考抽樣程序)在頻率軸(x軸)上的頻率范圍和分辨率取決于采樣速率和數據記錄的長度(采樣點數)。功率譜圖上的頻率點數或譜線數為N/2 ,N是信號采樣記錄中包含的點數。所有的頻點間隔為fSAMPLE/N ,通常稱之為頻率分辨率或FFT 分辨率：

　　Bin = fSAMPLE/N = 1 / (N · (tSAMPLE)

　　頻譜泄漏和窗函數

　　FFT分析中常常要用到窗函數。在基于FFT的測量中正確選擇窗函數非常關鍵。頻譜泄漏是由FFT算法中的假設造成的,FFT算法中假設離散時間序列可以精確地在整個時域進行周期延拓,所有包含該離散時間序列的信號為周期函數,周期與時間序列的長度相關。然而如果時間序列的長度不是信號周期的整數倍(fIN/fSAMPLE ( NWINDOW/NRECORD) ,假設條件即不成立,就會發生頻譜泄漏。絕大多數情況下所處理的是一個未知的平穩信號,不能保證采樣點數為周期的整數倍。頻譜泄漏使給定頻率分量的能量泄漏到相鄰的頻率點,從而在測量結果中引入誤差。選擇合適的窗函數可以減小頻譜泄漏效應。

　　為進一步了解窗函數對頻譜的影響,我們考察一下窗函數的頻率特性。輸入數據通過一個窗函數相當于原始數據的頻譜與窗函數頻譜的卷積。窗函數的頻譜由一個主瓣和幾個旁瓣組成,主瓣以時域信號的每個頻率成份為中心。旁瓣在主瓣的兩側以一定的間隔衰減至零。FFT產生離散的頻譜,出現在FFT每個譜線的是在每個譜線上的連續卷積頻譜。如果原始信號的頻譜成份與FFT中的譜線完全一致,這種情況下采樣數據的長度為信號周期的整數倍,頻譜中只有主瓣。沒有出現旁瓣的原因是旁瓣正處在窗函數主瓣兩側采樣頻率間隔處的零分量點。如果時間序列的長度不是周期的整數倍,窗函數的連續頻譜將偏離主瓣的中心,頻率偏移量對應著信號頻率和FFT頻率分辨率的差異,這個偏移導致了頻譜中出現旁瓣,所以,窗函數的旁瓣特性直接影響著各頻譜分量向相鄰頻譜的泄漏寬度。

　　窗函數特性

　　為簡化窗函數的選擇,有必要定義一些參數以便對不同的窗進行比較。這些參數有：-3dB主瓣帶寬、-6dB主瓣帶寬、旁瓣峰值、旁瓣衰減速度(表二)。

　　表二 常用的窗函數特性參數

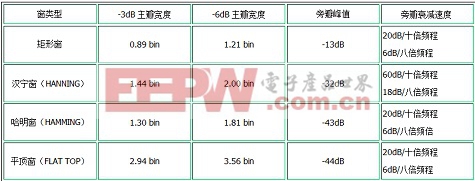
　　每種窗函數有其自身的特性,不同的窗函數適用于不同的應用。要選擇正確的窗函數,必須先估計信號的頻譜成份。如若信號中有許多遠離被測頻率的強干擾頻率分量,應選擇旁瓣衰減速度較快的窗函數;如果強干擾頻率分量緊鄰被測頻率時,應選擇旁瓣峰值較小的窗函數;如果被測信號含有兩個或兩個以上的頻率成份,應選用主瓣很窄的窗函數;如果是單一頻率信號,且要求幅度精度較高,則推薦用寬主瓣的窗函數。對頻帶較寬或含有多個頻率成份的信號則采用連續采樣。絕大多數應用采用漢寧(Hanning)窗即可得到滿意的結果,因為它具有較好的頻率分辨率和抑制頻譜泄漏的能力。

　　動態參數： SNR、 SINAD、 THD、SFDR與TTIMD

　　參照上述內容,由FFT可利用MATLAB軟件計算出功率譜、頻譜泄漏、窗函數、SNR、SINAD、THD、SFDR：

　　SNR=10*log10(Ps/Pn)

　　SINAD=10*log10(Ps/(Pn+Pd))

　　THD=10*log10(Pd/Ph(1))

　　SFDR=10*log10(Ph(1)/max(Ph(2:10)))

　　其中：Ps——信號功率、Pn——噪聲功率、Pd——由二到五次諧波引起的失調功率、Ph(1)——諧波功率(基波)、Ph(2:10)——二到九次諧波功率。

　　表三 信號頻譜與窗函數的選擇

　雙音互調(TTIMD)的測量非常巧妙,通過功率合成器將兩個輸入頻率相組合產生互調成份,用于模擬ADC的互調失真。選擇輸入頻率時必須考慮以下條件去優化互調性能：選擇輸入濾波器通帶以內的頻率;如果選擇的兩個輸入頻率非常接近時,還必須選擇正確的窗函數。然而如果頻率靠得太近,功率合成器會模擬二次和三次互調產生的全部互調分量;兩個輸入頻率相差太大時可能需要選用頻率分辨率較低的窗函數。

　　結論

　　在從高速ADC中捕獲信號并進行分析從而確定數據轉換器的動態性能時,需要考慮許多因素。理解基于FFT測量的基本知識和相關的計算、頻譜泄漏效應,了解如何借助適當的測試設備避免頻譜泄漏,掌握布線技巧就能成功地進行數據采集和分析。