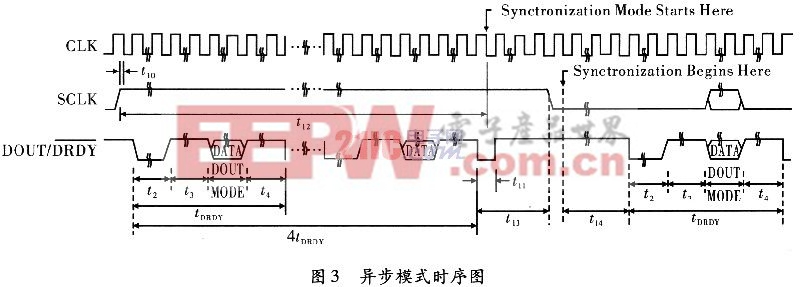
2．2 FPGA設計
FPGA的特點在于靈活，通用。如果資源夠用，可以實現各種數字組合，包括CPU。本系統采用的：FPGA是Ahera公司低價位的EP1C12，該芯片內含有兩個PLLs，12060LEs及239616 Total RAMbits。在本系統的設計中，FPGA內主要實現以下幾個功能：Kalman狀態控制信號、Kalm-an濾波運算、A／D控制模塊、時鐘及波特率設置等。卡爾曼濾波器的系統結構圖，如圖4所示。

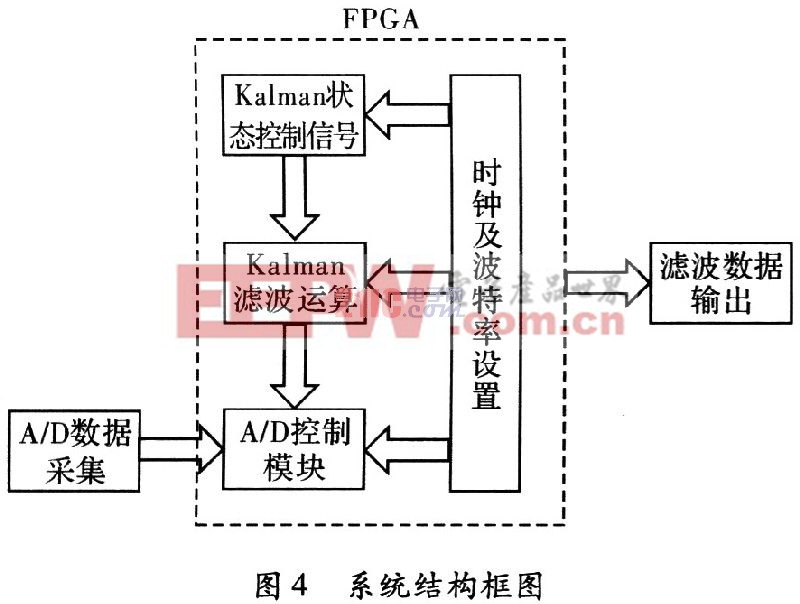
通過A／D轉換芯片采集轉換數據后，進入FPGA的A／D控制模塊，在Kalman狀態控制信號的作用下，進行濾波運算，然后通過控制接口將濾波數據輸出。由此可見，卡爾曼濾波的實現包括兩部分：Kalman狀態控制信號和Kalman濾波運算。

3 Kalmaft濾波器的設計
在FPGA中實現Kalman濾波器，重點在于平衡資源利用率和處理速度、數據運算精度之間的矛盾，難點在于浮點加、減、乘、除的硬邏輯及卡爾曼濾波流程控制的實現。一般地，實際應用中，數字采樣重復頻率是待采樣信號最高頻率成分的5倍以上能保證較好恢復原信號，本設計中出于后期升級的考慮，將采樣率設置在800次／s，是輸出信號帶寬的20倍。
通過第2節中的分解，Kalman濾波器由16次加法、20次乘法、1次除法以及必要的輸入、輸出及循環控制組成，共45步。狀態控制器(Kal-man狀態控制信號)實際是一個有限狀態機，分別控制濾波器中的45步運算，決定其執行順序，每一步利用計數器為其提供必要的時鐘周期。
Kalman濾波運算主要是浮點計算，浮點表示常用的標準是IEEE 754，IEEE二進制浮點數算術標準(IEEE754)是最廣泛使用的浮點數運算標準，為許多CPU與浮點運算器所采用。IEEE 754規定了4種表示浮點數值的方式：單精確度(32位元)、雙精確度(64位元)、延伸單精確度(43位元以上，較少使用)與延伸雙精確度(79位元以上，通常以80位元實做)。
二進制浮點數是以符號數值表示法格式儲存，將最高效位元指定為符號位元(Sign Bit)；“指數部分”，即次高效的e位元，為浮點數中經指數偏差(Exponent Bias)處理過后的指數；“小數部分”，即剩下的f位元，為有效位數(Significand)減掉有效位數本身的最高效位元，如圖5所示。

文中采用的單精度二進制小數，使用32個位元存儲，如圖6所示。

其中，31位是符號位；0表示正；1表示負；30～23位為階數；22～0表示數值的有效位。偏正值為+127。其表示的具體值可用式(27)表示

指數部分采用一個無符號的正數值存儲。單精度的指數部分是-126～+127加上127，指數值的大小為1～254(0和255是特殊值)。浮點小數計算時，指數值減去偏正值將是實際的指數大小。