降采樣FIR濾波器的設計與硬件實現
結合濾波器的階數可知式(1)中的h(n)可以表示為:
h(n)=-21×[δ(n)+δ(n-30)]-8l×[δ(n-1)+δ(n-29)]-58×[δ(n-2)+δ(n-29)]+…+6599×δ(n-15). (4)
于是,有:y(n)=-21×[x(n)+x(n-30)]-8l×[x(n-1)+x(n-29)]-58×[x(n-2)+x(n-29)]+…+6599×x(n-15). (5)
將以上各系數用(3)中的拆分結果替換,可將式(5)進一步寫為:
y(n)=-(16+4+1) [x(n)+x(n-30)]-(64+16+1) [x(n-1)+x(n-29)]-(64-8+2) [x(n-2)+x(n-29)]+…+(8192-2048+512-64+8-1)?x(n-15). (6)
這樣,輸出y(n)可表示成輸入移位相加減的形式。至此,抗混疊FIR濾波器便告設計完成。
由圖2可知,抗混疊濾波器輸出信號必須經過降采樣才能輸出。而對于本設計的濾波器,其降采樣率為2:l,理論上把式(6)取出一半即可滿足降采樣要求,但是,這樣就意味著之前浪費了一部分硬件資源去計算這一半不用的數據。基于此考慮,在設計濾波器時可加上一個降采樣控制器,x(n)還是正常輸入,每一拍進一個新的采樣點,而濾波過程則用降采樣控制器控制,這樣可使計算每隔一拍進行一次。本文引用地址:http://www.j9360.com/article/191625.htm
3 仿真結果分析
3.1 濾波器的幅頻響應
圖5所示是在matlab中利用定點化之后的濾波器系數畫出濾波器的幅頻響應特性曲線。
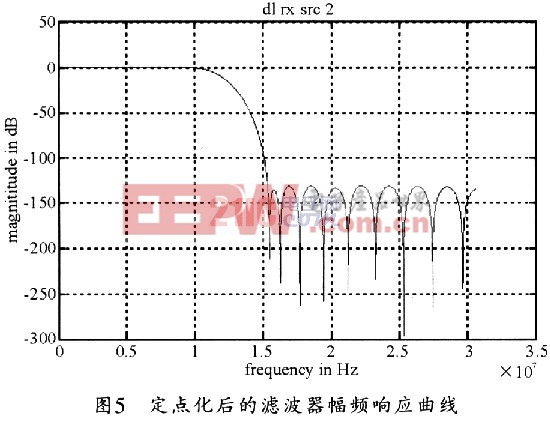
該曲線與2.1中設計的濾波器幅頻曲線基本一致,從而驗證了本設計的正確性。
3.2 硬件代碼的仿真波形
對于本文中設計的硬件架構,用Verilog語言寫出相應的硬件實現代碼,再用modelsim軟件進行波形仿真,其仿真結果如圖6所示。

濾波器相關文章:濾波器原理
濾波器相關文章:濾波器原理












評論