整數倍頻率偏移估計模塊

將相關單元輸出的復數據的實虛部符號位送到整數倍頻偏估計單元中進行整數倍頻偏估計。為了節省芯片資源，這里我們將估計整數倍頻偏的算法加以簡化，用相關后的復數據在導頻位置上的實虛部的符號位來估計整數倍頻偏值。下面的仿真的電路波形圖證明這樣實現整偏估計算法是可行的。它的輸入為相關單元輸出的復數據實虛部的符號位和此復數據的載波同步位置，輸出為整數倍頻偏估計值。

小數倍頻率偏移和采樣鐘頻率偏移模塊

首先對相關單元模塊輸出的復數據的實虛部進行歸一化，然后求歸一化單元輸出的16位復數據的相角，同時用RAM的讀地址和讀使能信號分別控制讀取存有矢量A和矢量B數據的ROM表中的數據。其中矢量A和B分別為線性最小平方估計算法中矩陣AT的第一行和第二行矢量，用此相角分別和讀出的矢量A和矢量B在一個符號內進行相乘累加，再根據保護間隔的不同，乘以相應的系數，便可分別得到小數倍頻偏和采樣鐘頻率偏移的估計值。

細定時估計模塊

考慮到定時估計范圍的問題，該模塊利用四個符號的散布導頻進行定時估計。將當前符號的散布導頻值及從RAM中讀出的前三個符號的散布導頻值按一定順序排列，并做相鄰導頻相關。將相關后的復數據的實虛部分別取絕對值累加，并將二者的累加和進行歸一化處理后進行查表，從而得出復數的相位值。這個相位即為符號定時偏移所引起的旋轉相位。再對此相位做如公式(6)的運算，這樣就得到了符號定時偏移的整數和小數部分的和，然后將其送到求整函數中，從而得到符號定時偏移的整數部分。將這個值經過并/串變換后送到前端時域同步部分，去調整FFT窗位。

電路仿真

其仿真條件為：瑞利信道，SNR為15dB，載波頻偏設為-14.9倍子載波間隔(即整數倍頻偏值為-15，小數倍頻偏值為0.1倍子載波間隔)，采樣鐘偏移為50ppm，保護間隔長為512，定時符號偏移為-100個采樣點。此電路工作頻率為10MHz。輸入的16位復數據由MATLAB仿真程序產生的。

整數倍頻率偏移電路仿真

由于電路波形中無法表示小數，因此將各小數進行“擴展”，其表示皆為二進制數據，以下同。在圖4.1中，out_re[31]和out_im[31]分別是前后兩個OFDM符號中對應子載波相關結果的實虛部的符號位，int_freqoffset[5..0]和syn_int分別是整數倍頻偏估值和其有效起始位置脈沖。

圖4.1 整數倍頻偏估計部分的電路仿真波形圖

由于整數倍頻偏在每一符號的結束處才能估計出來，所以syn_int在每一個符號的結束處出現，其后即為當前符號的整數倍頻偏值。由于本算法利用了4個符號的連續導頻，故圖4.1中，從第四個syn_int后的int_freqoffset[5..0]才是當前符號的整數倍頻偏估計值。由仿真波形可看出，估出的整數倍頻偏與仿真數據中所假設的一致。故用此算法的簡化形式可以準確地估計出整數倍頻偏值。

小數倍頻率偏移及采樣鐘頻率偏移估計的電路仿真

sernum[1..0]表示前級輸入的符號類型;syn為輸入復數據中的有用數據起始脈沖;rein[15..0]和imin[15..0]分別為FIFO模塊輸出復數據的實虛部;syn_offset為小數倍頻偏和采樣鐘偏移估計結果的起始位置;fri[14..0]和qdelt[14..0]為小數倍頻偏估計值和采樣鐘偏移估計值，它們由1位符號位和14位小數位組成。這里的小數位數是根據其估計范圍和估計精度要求來確定的。

在圖4.2中，小數倍頻率偏移和采樣鐘頻率偏移估計模塊使用連續導頻進行估計。在每個符號末，syn_offset高電平有效時，fri[14..0]和qdelt[14..0]才是當前符號的小數倍頻率偏移和采樣鐘頻率偏移估計值。波形中的估值與實際數據的對應關系如表4.1所示。

圖4.2 小數倍頻偏和采樣鐘偏移估計單元的電路仿真波形圖

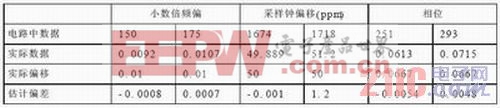
表4.1 波形圖中數據與實際數據對照表

小數倍頻率偏移和采樣鐘頻率偏移模塊是在整偏校完之后才有效，此時的小數倍頻率偏移是經過時域粗偏估計校正后的剩余部分。表4.1列出波形中的估值與實際數據的對應關系。從表中的數字對應關系可以看出，電路中估計的小數倍頻偏與實際頻偏的差在0.1%以內。采樣鐘偏移估計值與實際偏移誤差為1ppm左右，這已滿足了采樣鐘的粗調精度;相位輸出為前后符號的小數倍偏頻所引起的相位旋轉。由此單元電路，可以準確地估計出小數倍頻偏和采樣鐘偏移及其相位。