Hopfield網絡求解TSP兩種改進算法的仿真研究
用Hopfield神經網絡求解旅行商問題(TSP),給組合優化完備性問題的求解提供新的方法。但該算法會經常生成無效解,因此需進一步改進。有學者通過TSP網絡的動態分析修正TSP的能量函數,從而獲得有效解,但其能量函數的表達式過于復雜。有人簡化該能量函數,進一步提出改進算法。這里擬對典型的兩種改進算法進行仿真分析。
2 HopfieId網絡的能量函數
為將TSP問題映射成神經網絡的動態過程,Hopfield采取置換矩陣的表示方法,用N×N個神經元組成Hopfield人工神經網絡表示商人訪問N個城市。
網絡達到穩定狀態時各神經元的狀態對應置換矩陣各元素的值(“1”或“0”)。用uxi表示神經元(x,i)的輸出,相應的輸入用Vxi表示。
若城市x在i位置上被訪問,則Vxi=1,否則Vxi=0。Hop-field定義如下形式的能量函數:
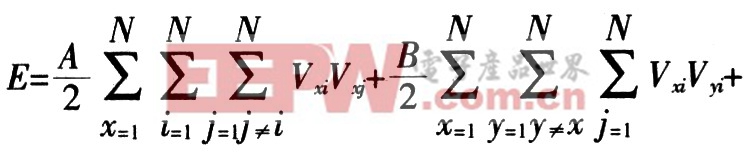
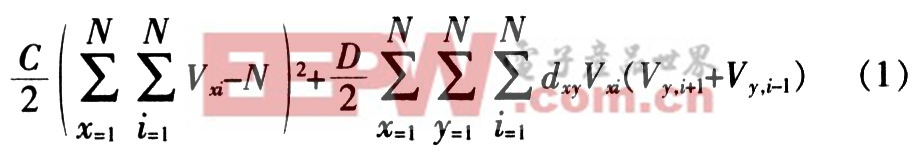
式中,A、B、C、D是實系數。dxy為城市x與y之間的距離。
式中前3項是問題的約束項。最后1項是優化目標項。利用動態方程:
![]()
式中,VT表示V的轉置。
求得A、B、C、D和d描述的連接矩陣和及偏置,的表達式:
Hopfield把能量函數的概念引入神經網絡,從而開創求解優化問題的新方法。但該算法會以大百分比生成無效解,因此需進一步改進。
3 改進算法與仿真
3.1 改進算法1
Aiyer等人從理論上證明Hopfield網絡不能生成有效解的原因,并提出一個新的連接矩陣:
外部輸入
可從理論上證明該算法的有效性,試驗也驗證它幾乎100%可獲得有效解。利用上述改進算法對Hopfield的10城市問題進行模擬試驗,已知其最短路徑為2.690 6。模擬試驗采用兩種神經元狀態更新函數,一種采用S型函數,即
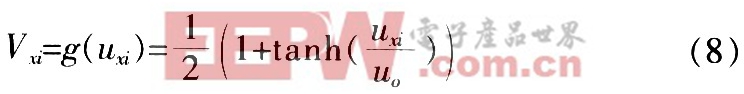
另一種采用如下定義的軟限幅函數:
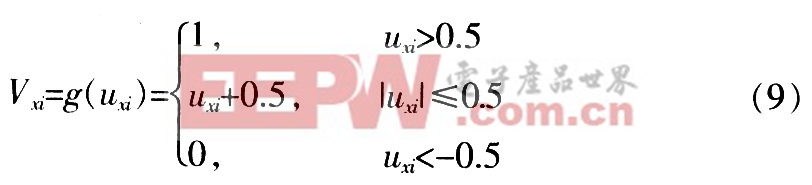








評論