摘要：對于無片外大電容的低壓差線性穩壓器來說，用建立小信號模型來分析系統傳輸函數從而推出零極點分布的方法過于復雜繁瑣，本文提出一種簡化電路分析方法，可以不用復雜的化簡和計算就可以得出LDO的零極點位置分布，并通過幾種LDO頻率補償方式為例介紹該方法的應用，最后通過仿真驗證了此方法的準確性。

　　引言

　　對于全片內LDO而言，由于沒有片外大電容，故很大程度上LDO的穩定性成為全片內LDO設計的難點。而頻率特性是衡量穩定性的重要指標，只有清楚電路的零極點的位置分布，才可以對LDO的穩定性進行補償，最常見的方法就是通過建立小信號模型，利用KCL和KVL等定理對各個方程式進行化簡，得出系統傳輸函數，但這種方法需要的計算量比較大，隨著補償電容和級數的增加，計算會越來越繁瑣，不利于快速分析。本文的工作主要是提出一種通過利用簡化框圖的結構，該結構在分析極點和零點時各采用不同假設從而得到不同的電流通路，可以快速分析出LDO系統零極點的分布情況，最后并通過仿真驗證了該方法的可靠性。

　　傳統的小信號分析方法

　　如圖1所示，普通無片外電容LDO結構一般由誤差放大器(EA)，調整管MP以及電阻反饋網絡RF1、RF2組成，CL是一個容值很小的電容，對于片內集成的LDO來說，一般只有1pF~50pF左右。以密勒補償為例，采用傳統的小信號分析方法，如圖2。　　

 

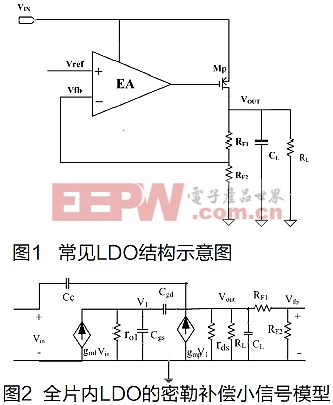
　　其中個g_m1和r_o1分別為誤差放大器的跨導和輸出電阻，g_mp和r_ds分別為調整管的跨導和溝道電阻，C_gs和C_gd分別為調整管的柵源電容和柵漏電容，C_c為密勒補償電容。根據KVL和KCL定理可得如下關系：