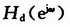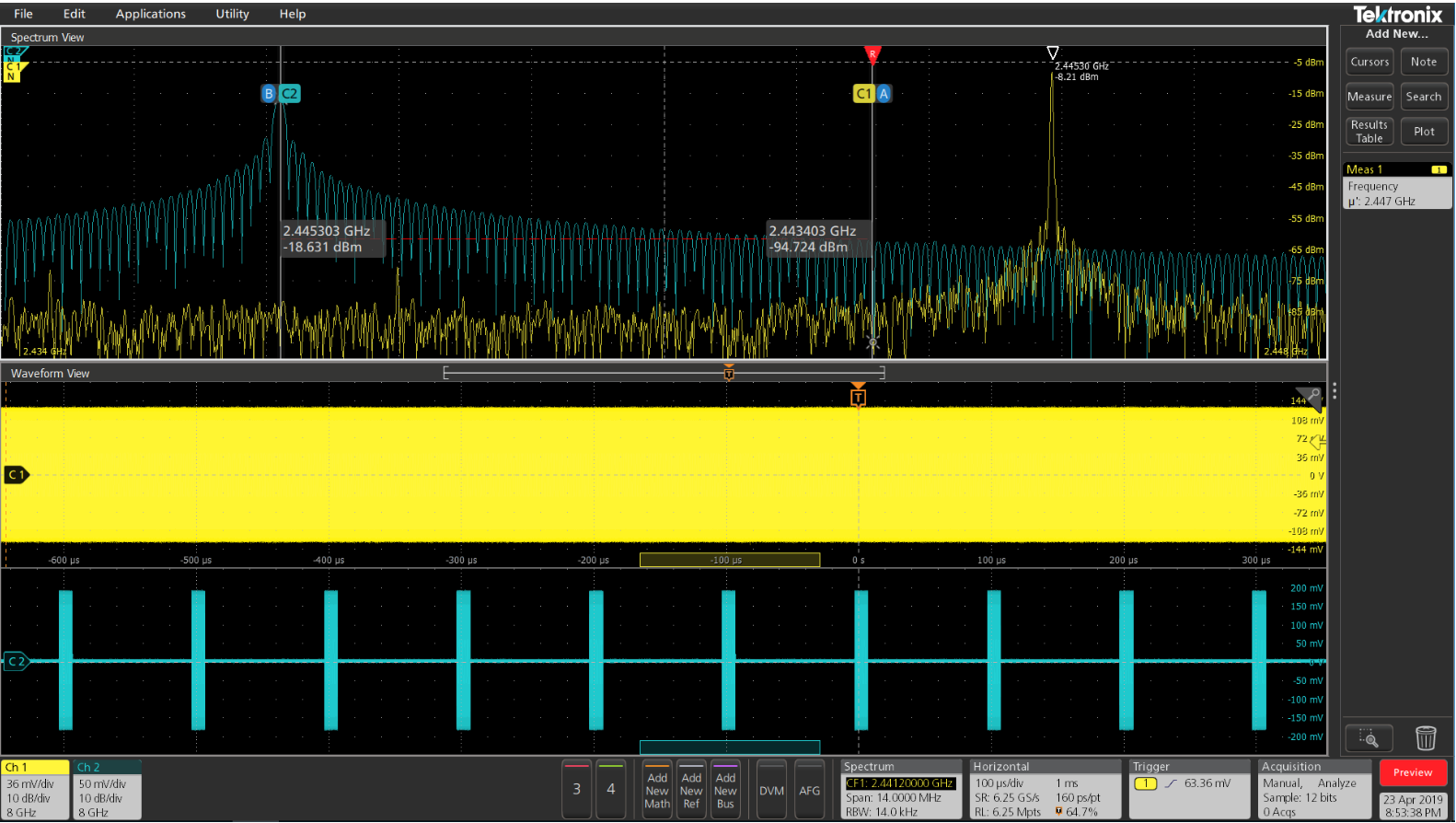
- 快速傅里葉變換 (fast Fourier transform) 簡稱FFT, 是利用計算機計算離散傅里葉變換(DFT)的高效、快速計算方法的統稱。快速傅里葉變換是1965年由J.W.庫利和T.W.圖基提出的。采用這種算法能使計算機計算離散傅里葉變換所需要的乘法次數大為減少,特別是被變換的抽樣點數N越多,FFT算法計算量的節省就越顯著。一直以來,我們接受的教育就是要用FFT來進行頻域信號的測試與分析。工作以后我們利用示波器上的FFT功能進行頻域信號測試。FFT功能在示波器普及率高,易獲取。可以實現時域、頻
- 關鍵字:
傅里葉變換 示波器 多通道分析
- 1.4 傅立葉級數展開 之前我們在介紹泰勒展開式的時候提到過傅立葉級數。利用傅立葉級數對函數進行展開相比于泰勒展開式,會具有更好的整體逼近性,而且對函數的光滑性也不再有苛刻的要求。傅立葉級數是傅立葉變換的基礎,傅立葉變換是數字信號處理(特別是圖像處理)中非常重要的一種手段。遺憾的是,很多人讀者并不能較為輕松地將傅立葉變換同高等數學中講到的傅立葉級數聯系起來。本節我們就來解開讀者心中的疑惑。 如果你對本文涉及的基礎問題不甚了解,那么建議你閱讀本文前面的部分。希望讀者能日積月累,夯實基礎。
- 關鍵字:
傅里葉變換 小波
- 這一系列的文章中間中斷了很久,很多朋友也留言希望我繼續連載完,遂“重拾舊河山”,希望如果有時間能夠把它做完。 本節我們介紹歐拉公式,它是復變函數中非常重要的一個定理,同時對于傅立葉變換的理解也必不可少。我們在高等數學里學習的傅立葉級數通常都是用三角函數形式表示的,而傅立葉變換中的一般都是用冪指數形式的,歐拉公式的作用正是把三角函數與e的冪指數聯系到一起。 如果你對本文涉及的基礎問題不甚了解,那么建議你閱讀本文前面的部分。 完全搞懂傅里葉變換和小波(1)——總綱 http://www.eepw.
- 關鍵字:
傅里葉變換 小波
- 書接上文,之前我們介紹了高等數學里的三個中值定理,本節我們繼續按照總綱的思路,用柯西中值定理來證明泰勒公式。這是我們循序漸進引出傅里葉的最后一項任務,完成這一步的學習之后,你就可以從級數的角度,了解傅里葉的意義了。 完全搞懂傅里葉變換和小波(1)——總綱 http://www.j9360.com/article/201703/344766.htm 完全搞懂傅里葉變換和小波(2)——三個中值定理 http://www.j9360.com/article/201702/344594.htm
- 關鍵字:
傅里葉變換 小波
- 書接上文,本文章是該系列的第二篇,按照總綱中給出的框架,本節介紹三個中值定理,包括它們的證明及幾何意義。這三個中值定理是高等數學中非常基礎的部分,如果讀者對于高數的內容已經非常了解,大可跳過此部分。當然如果你需要對傅里葉變換有一個更深刻的認識,或者說從數學角度一點一滴完全搞懂它,為了體系的完整性,這部分知識還是必須的。 上篇文章鏈接地址:完全搞懂傅里葉變換和小波(1)——總綱 http://www.j9360.com/article/201702/344594.htm 由于公式較多,這里只能
- 關鍵字:
傅里葉變換 小波
- 無論是學習信號處理,還是做圖像、音視頻處理方面的研究,你永遠避不開的一個內容,就是傅里葉變換和小波。但是這兩個東西其實并不容易弄懂,或者說其實是非常抽象和晦澀的! 完全搞懂傅里葉變換和小波,你至少需要知道哪些預備知識?主頁君從今天開始就將通過一些列文章告訴你他們之間的來龍去脈!本節是全部系列文章的第一節——總綱,日后我們也將按照這個思路一點一點講述所有的知識。需要說明的是,本文主要面向計算機專業或者電子信息專業的讀者,為此我們將盡量采取一些非常非常基礎的知識來幫助你理解。所以,題目里面講的“完全搞懂
- 關鍵字:
傅里葉變換 小波
- 隨著超聲波技術的發展,超聲波在風速測量、流體的流速和流量的測量中起到了重要作用。目前,采用超聲波進行風速測量的方法主要有超聲波時差法、多普勒法、相關法、卡門渦街原理、相位差法和超聲波頻率差法。超聲波時
- 關鍵字:
風速風向 DSP 相關函數 傅里葉變換
- 傅里葉變換在物理學、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的應用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值分量和頻率分量)。
傅里葉變換能將滿足一定條件的某個函數表示成三角函數(正弦和/或余弦函數)或者它們的積分的線性組合。在不同的研究領域,傅里葉變換具有多種不同的變體形式,如連續傅里葉變換和離散傅里葉變換。
傅里葉變換是一種解決問題的方法,一種工具,一種看待問題的角度。理解的關鍵是:一個連續的信號可以看作是一個個小
- 關鍵字:
傅里葉變換 拉普拉斯變換
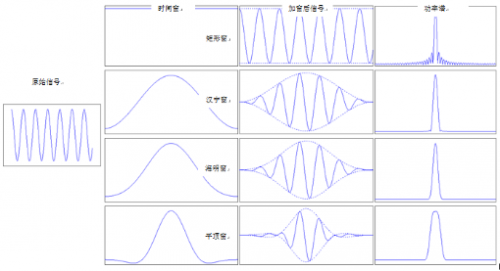
- 摘要:在信號分析時,我們一般會截取有限的波形數據做傅里葉變換,這個截斷過程會產生泄漏,導致功率擴散到整個頻譜范圍,產生大量“霧霾數據”,無法得到正確的頻譜結果。雖然知道加窗可以抑制泄漏,但復雜的窗函數表達式及抽象的主瓣旁瓣描述方法,另人更加迷惑,下面我們拋棄公式用通俗易懂的方式介紹窗函數的選擇。 1.加窗與窗函數 在數字信號處理中,常見的有矩形窗、漢寧窗、海明窗和平頂窗,這里不再贅述窗函數的表達式,只討論窗函數的使用,下圖直觀地描述了信號加窗的過程及窗函數基本特征。
- 關鍵字:
窗函數 傅里葉變換
- 簡介:本文介紹了在實際工程中常用到的傅里葉變換和Z變換之間的關系、各自的意義等內容。
傅里葉變換在物理學、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的應用(例如在信號處理中,傅里葉變換的典型用途是將信號分解成幅值分量和頻率分量)。
傅里葉變換能將滿足一定條件的某個函數表示成三角函數(正弦和/或余弦函數)或者它們的積分的線性組合。在不同的研究領域,傅里葉變換具有多種不同的變體形式,如連續傅里葉變換和離散傅里葉變換。
傅里葉變換是一種
- 關鍵字:
傅里葉變換 拉普拉斯變換 變換

- 學習傅里葉變換需要面對大量的數學公式,數學功底較差的同學聽到傅里葉變換就頭疼。事實上,許多數學功底好的數字信號處理專業的同學也不一定理解傅里葉變換的真實含義,不能做到學以致用!
事實上,傅里葉變換的相關運算已經非常成熟,有現成函數可以調用。對于絕大部分只需用好傅里葉變換的同學,重要的不是去記那些枯燥的公式,而是解傅里葉變換的含義及意義。
本文試圖不用一個數學公式,采用較為通俗的語言深入淺出的闡述傅里葉變換的含義、意義及方法,希望大家可以更加親近傅里葉變換,用好傅里葉變換。
一偉大的傅
- 關鍵字:
傅里葉變換
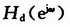
- 有限長脈沖響應(FIR)數字濾波器由于設計靈活,濾波效果好以及過渡帶寬易控制,因此在數字信號處理領域得到了廣泛的應用。FIR數字濾波器的典型設計方法主要有窗函數法和頻率采樣法。正確理解和掌握這兩種設計方法是學習FIR數字濾波器的一個重要環節。用窗函數法進行FIR濾波器設計的相關問題,目前的教材講解較為細致,這里不再贅述。本文主要探討用頻率采樣法設計FIR數字濾波器的相關問題,主要包括設計原理、性能分析、線性相位條件及設計中應注意的問題等幾個方面。
1 設計原理及濾波器性能分析
頻率采樣法是
- 關鍵字:
FIR濾波器 傅里葉變換
- 近紅外光譜分析技術近年來巳成功應用于食品、煙草、藥品及化工等諸多行業產品的分析測定,特別在農副產品的品...
- 關鍵字:
傅里葉變換 紅外光譜分析 化學測定
- 摘要 基于Good—Thomas映射算法和ISE快速傅里葉變換IP核,設計了一種易于FPGA實現的24點離散傅里葉變換,所設計的24點DFT模塊采用流水線結構,主要由3個8點FFT模塊和1個3點DFT模塊級聯而成,并且兩級運算之間不
- 關鍵字:
FPGA 離散 傅里葉變換 結構設計
傅里葉變換介紹
傅里葉變換-正文 一種積分變換,它來源于函數的傅里葉積分表示。積分
(1)
稱為? 的傅里葉積分。周期函數在一定條件下可以展成傅里葉級數,而在(-∞,∞)上定義的非周期函數?,顯然不能用三角級數來表示。但是J.-B.-J.傅里葉建議把?表示成所謂傅里葉積分的方法。 設?(x)是(-l,l)上定義的可積函數,那么在一定條件下,?(x)可以用如下的傅里葉級數來表示:
(x [
查看詳細 ]
關于我們 -
廣告服務 -
企業會員服務 -
網站地圖 -
聯系我們 -
征稿 -
友情鏈接 -
手機EEPW
Copyright ?2000-2015 ELECTRONIC ENGINEERING & PRODUCT WORLD. All rights reserved.
《電子產品世界》雜志社 版權所有 北京東曉國際技術信息咨詢有限公司

京ICP備12027778號-2 北京市公安局備案:1101082052 京公網安備11010802012473