數字控制式LLC諧振變換器建模分析與驗證
摘要:針對半橋LLC諧振變換器的建模及其驗證展開分析,同時分析了數字控制對系統穩定性造成的影響,并給出采用數字控制時系統穩定性的解決方案。首先,通過擴展函數描述法得到傳統的模擬域數學模型,并在Saber中搭建仿真模型,利用小信號分析法驗證該數學模型的準確性,從而得出得到的系統數學模型具有參考性,由此提供了環路設計的基礎;其次,采用數字控制,考慮到其離散特性,分析了數字控制對系統穩定性的影響,并通過Matlab仿真驗證了該理論的正確性,最終設計出性能良好的數字PID補償器;最后,針對實際應用場合,搭建實驗平臺,進行相關實驗驗證。
本文引用地址:http://www.j9360.com/article/276365.htm前言
現今蓄電池充電器常用的充電拓撲有正激、Buck、Boost以及各種形式的諧振變換器,而諧振變換器憑借其軟開關特性得到更加廣泛的應用,其中半橋LLC諧振變換器結構簡單,允許空載運行并具有較寬的輸入電壓范圍,且通過磁集成技術可以提高整機的功率密度,具有明顯的優勢,因此文中選用半橋式LLC諧振變換器作為研究對象。此外,由于數字控制具有元器件少、控制靈活、容易實現復雜控制算法優點,所以文中選用數字控制。
蓄電池充電器主要工作于恒流或恒壓輸出模式,要求變換器具有良好的穩態跟蹤性能,并且考慮到蓄電池在充電過程中,其所需要的充電電流會不斷變化,即蓄電池負載并非始終保持恒定,此要求變換器具有較好的動態性能,能夠較快跟蹤到參考電流變化,而現在市場上的變換器不具備以上特性,所以需要對變換器的控制環路進行設計優化。首先采用擴展函數描述法[1]對其進行建模,得到開環數學模型,并驗證該模型的準確性;其次,分析數字控制帶來的計算延時、控制延時對傳統數學模型穩定性的影響,并給出相應的解決方案并設計數字PID補償器;最后根據實際應用參數,進行仿真和實驗驗證。
1 系統環路設計
1.1 擴展函數描述法建模
由于諧振變換器的諧振特性,其狀態變量中含有許多開關頻率處的信息,傳統的狀態空間平均法不再適用,因此采用擴展函數描述法(EDF)建立半橋LLC諧振變換器的數學模型。如圖1所示為半橋式LLC諧振變換器原理圖。
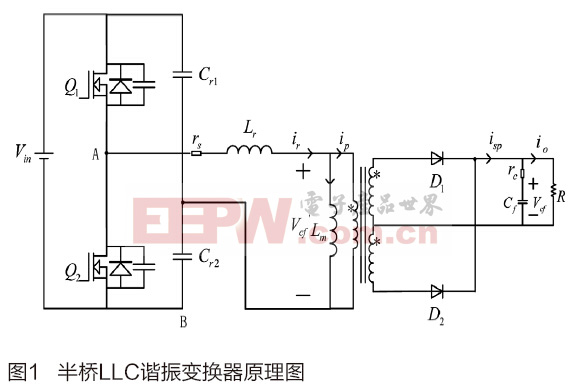
首先,選擇激磁電感電流、諧振電感電流以及諧振電容電壓作為狀態變量,并根據拓撲結構,列寫非線性時變狀態方程:
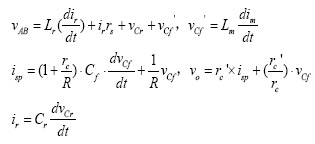 (1)
(1)
式(1)中:Lr為諧振電感,Lm為激磁電感、Cr1、Cr2為諧振電容。
其次,根據Fourier分解[2]將周期信號分解為正弦函數之和,只考慮基波分量,得到所需的近似大信號模型,系統穩態運行后,變量不隨時間變化而變化,因此忽略模型中的時變分量,即可得到穩態工作點求解方程并轉化成矩陣形式,最后在穩態工作點附近,進行變量分離,獲取系統的小信號數學模型,并表示成矩陣形式。
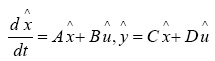 (2)
(2)
其中,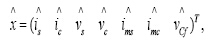
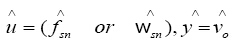

通過以上過程可以得到輸出電壓對開關頻率的關系矩陣:
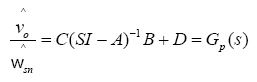 (3)
(3)
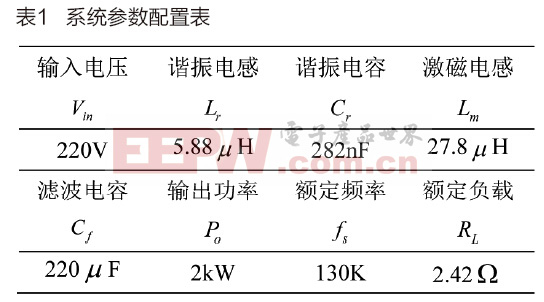
為進行環路設計,首先需要驗證上述方法得到的數學模型的準確性,如表1所示為實際系統參數。
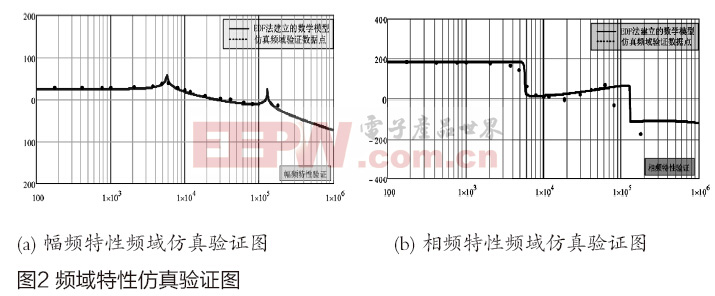
在Saber中搭建仿真模型,逐點仿真。仿真驗證結果如圖2所示。
為了獲得良好的系統動態和穩態特性,需加入補償環節,因考慮系統的寄生參數[2]后,系統階數較高,因此在設計補償環路時,通過加入適當的零極點,來改善系統的頻域特性。本文采用PID控制器[3],為實現零極點對消,將PID控制的表達式表示成:
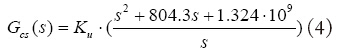
pid控制相關文章:pid控制原理
dc相關文章:dc是什么
pid控制器相關文章:pid控制器原理
調壓器相關文章:調壓器原理


評論