乘法器與調制器
雖然許多有關調制的描述都將其描繪成一種乘法過程,但實際情況更為復雜。
首先,為清晰起見,若信號Acos(ωt)和未調制的載波cos(ωt)施加于理想乘法器的兩路輸入,則我們將得到一個調制器。這是因為兩個周期波形Ascos(ωst)和Accos(ωct)施加于乘法器(為便于分析,假定比例因子為1 V)輸入端,產生的輸出為:

但在大多數情況下,調制器是執行此功能更好的電路。調制器(用來改變頻率的時候也稱為混頻器)與乘法器密切相關。乘法器的輸出是其輸入的瞬時積。調制器的輸出是該調制器其中一路輸入的信號(稱為信號輸入)和另一路輸入的信號符號(稱為載波輸入)的瞬時積。圖1顯示了調制函數的兩種建模方法:作為放大器使用,通過載波輸入上的比較器輸出切換正增益和負增益;或者作為乘法器使用,并在其載波輸入和其中一個端口之間放置一個高增益限幅放大器。兩種架構都可用來形成調制器,但開關放大器架構(用于AD630平衡調制器中)運行較慢。大多數高速IC調制器含有一個跨導線性乘法器(基于吉爾伯特單元),并在載波路徑上有一個限幅放大器,用來過驅其中一路輸入。該限幅放大器可能具有高增益,允許低電平載波輸入——或者具有低增益和干凈的限幅特性,從而要求相對較大的載波輸入以正常工作。
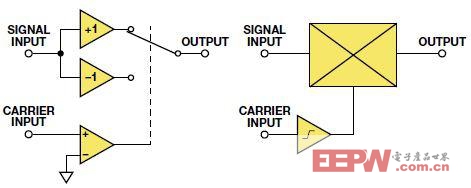
圖1.調制函數的兩種建模方法
出于某些原因,我們使用調制器而非乘法器。乘法器的兩個端口均為線性,因此載波輸入的任何噪聲或調制信號都會與信號輸入相乘,降低輸出;同時,大多數情況下可忽略調制器載波輸入的幅度變動。二階特性會導致載波輸入的幅度噪聲影響輸出,但最好的調制器都會盡可能減少這種影響,因此不納入本文的討論范圍。簡單的調制器模型使用由載波驅動的開關。(理想)開路開關具有無限大的電阻和零熱噪聲電流,且(理想)閉路開關具有零電阻和零熱噪聲電壓;因此,雖然調制器的開關并非理想,但相比乘法器而言,調制器依然具有較低的內部噪聲。另外,比起乘法器,設計與制造類似的高性能、高頻率調制器也更為簡便。
與模擬乘法器相同,調制器將兩路信號相乘;但與模擬乘法器不同的是,調制器的乘法運算是非線性的。當載波輸入的極性為正時,信號輸入乘以+1;而當極性為負時,則乘以-1.換言之,信號乘以載波頻率下的方波。
頻率為ωct的方波可使用傅里葉序列的奇次諧波表示: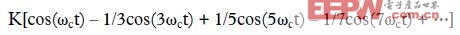
對該序列求和:[+1, -1/3, +1/5, -1/7 + ……]其值為π/4.因此,K數值為4/π,這樣當正直流信號施加到載波輸入時,平衡調制器可作為單位增益放大器使用。
載波幅度并不重要,只要它足夠大,可驅動限幅放大器即可;因此,由信號Ascos(ωst)和載波cos(ωct)驅動的調制器產生的輸出即為信號與載波平方的乘積:
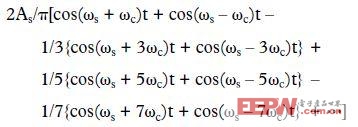
該輸出包含下列項的頻率之和與頻率之差:信號與載波、信號與載波的所有奇次諧波。理想的完美平衡調制器中不存在偶次諧波乘積。然而在真實調制器中,載波端口的殘余失調會導致低電平偶次諧波乘積。在許多應用中,低通濾波器(LPF)可濾除高次諧波乘積項。請記住,cos(A) = cos(-A),因此cos(ωm - Nωc)t = cos(Nωc -ωm)t,并且無需擔心“負”頻率。濾波處理后,調制器輸出可計算如下:
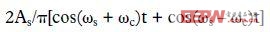
它和乘法器輸出的表達式一致,只是增益稍有不同。在實際系統中,增益采用放大器或衰減器進行歸一化,因此此處無需考慮不同系統的理論增益。
在簡單的應用中,顯然使用調制器優于使用乘法器,但如何定義“簡單”?調制器用作混頻器時,信號與載波分別為頻率等于f1和fc的簡單正弦波,未經濾波處理的輸出包含頻率和( f1 + fc)與頻率差( f1 - fc),以及信號與載波奇次諧波的頻率和與頻率差( f1 + 3fc)、( f1 - 3fc)、( f1+ 5fc)、( f1 - 5fc)、( f1 + 7fc)、( f1 - 7fc)…。經LPF濾波之后,預計僅得到基波項( f1 +fc)和(f1 -fc)。
然而,若( f1 + fc) > ( f1 - 3fc),將無法使用簡單的LPF區分基波與諧波項,因為某個諧波項的頻率低于某個基波項。這并非屬于簡單的情況,因此需進一步分析。



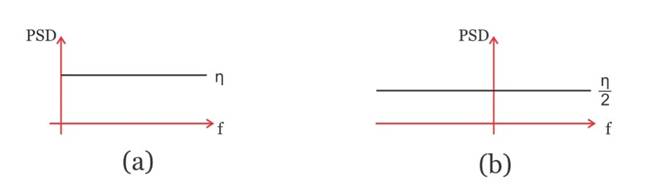

評論