1.引言

近年來，能源短缺和環境問題越來越受到人們關注，新能源的開發利用越來越受到人們重視。風力發電由于風速的可再生、清潔無污染等特點成為目前世界上增長最快的可再生能源。風速預測的準確性直接關系到風電場對電力系統的影響，同時也為風電機組的控制提供了重要依據。因此提高風速預測的準確性，對于增加電網的可靠性、提高經濟效益有很重要的意義。

在現實中，大多數時間序列都是非平穩的，因此仿真建模前需對實際數據進行差分處理，雖然差分后可將數據看作是是平穩序列，然而經驗證可知，其中仍含有非平穩部分，這就造成了ARIMA預測非平穩時間序列的誤差增大。為提高風速數據中非線性部分的預測精度，本文提出了一種基于ARIMA和改進Elman神經網絡組合模型對某地區風速進行預測的新方法。ARIMA模型用于描述歷史數據的線性關系，改進的神經網絡模擬數據的非線性規律。

本文采用2009年9月的720個風速數據建立組合預測模型，并利用該模型預測10月1日到6日內144個風速，取得了比較滿意的預測效果。

2.ARIMA-Elman模型原理

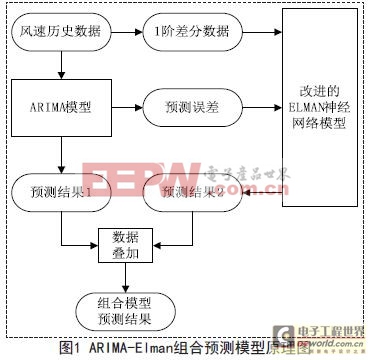
組合模型原理如圖1所示。對于波動性較大的風速數據而言，單一的時間序列預測具有較大的滯后，而差分后的時間序列能夠反映原始數據變化趨勢，具有一定的預知性。然后用改進Elman神經網絡，以ARIMA預測誤差和歷史風速1階差分序列作為網絡輸入，預測ARIMA模型的誤差，使非線性規律包含在改進Elman神經網絡的預測結果中。最后使用ARIMA的預測結果與改進Elman神經網絡的誤差預測結果相疊加得到組合預測模型的預測值。

3.ARIMA模型

3.1 模型的概念

時間序列模型分為平穩時序模型和非平穩時序模型。平穩時序模型包括自回歸(Auto-Regressive,AR)模型、滑動平均(MovingAverage,MA)模型和自回歸移動平均(Auto-Regressive and Moving Average,ARMA)模型。工程上最常用的非平穩模型是差分自回歸移動平均(Autoregressive Integrated MovingAverage,ARIMA)模型。其中ARIMA(p,d,q)模型的表達式記為：

3.2 模型建立

①數據的預處理

采用時間序列進行仿真預測可以大大降低預測的工作量，論文使用某一臺風機的風速數據，首先對時間序列用自相關函數法檢驗平穩性，經1階差分后，滿足時間序列平穩性要求，即差分階數d=1.

②模型定階與參數估計

目前常使用最佳準則函數進行定階，其包括最小FPE、AIC和SBC準則。本文采用AIC準則，即最小信息量準則，利用似然函數估計值最大值原則來確定模型p、q階數分別為2、1,即ARIMA(2,1,1)。模型定階后，利用最小二乘法，使殘差平方和達到最小的那組參數值即為模型參數估計值[7].

3.3 評價標準

本文采用平均絕對百分比誤差(MAPE)、平方和誤差(SSE)以及均方根誤差(RMSE)對預測結果進行評價，計算公式如下：

4.改進的Elman神經網絡

4.1 改進Elman神經網絡原理

Elman神經網絡是一種具有局部記憶單元和局部反饋連接的前向反饋網絡。本文采用一種改進的Elman神經網絡，其非線性狀態空間表達式為：

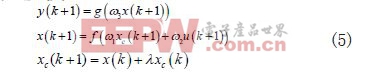
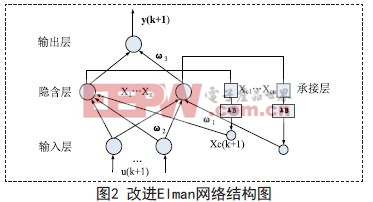
如圖2所示，在承接層部分引入前一時刻c x 值，B為一步延遲算子，其增益用λ 表示，其大小反映承接層對過去時刻記憶的強弱。