4.2.1.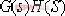 的二種表達式 的二種表達式
⒈系統方塊圖:如圖4-3 所示。
2.: 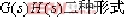 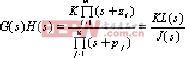
注:
(1).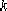 ………開環放大系數,增益,傳遞系數。 ………開環放大系數,增益,傳遞系數。 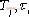 ……時間常數。 ……時間常數。
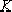 ………開環零極點形式的傳遞系數。 ………開環零極點形式的傳遞系數。
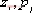 ……開環零點、極點的負值。 ……開環零點、極點的負值。
(2).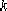 與 與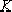 與關系: 與關系: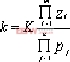 4.2.2 特征方程D(s)=0 的幾種表達形式:
⒈.閉環傳遞函數的幾種形式:
⑴.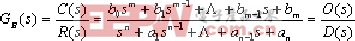
⑵.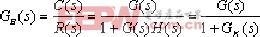
⒉" 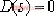 " 的幾種形式: " 的幾種形式: ⑴. 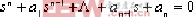
⑵. 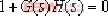
⑶.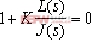
⑷. 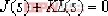
⑸.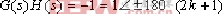 (k=0,1,2,3,……) (k=0,1,2,3,……)
⑹.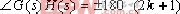 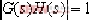
4.2.3繪制根跡的數學依據:
⒈. 幅角條件,幅值條件--幅相條件:
⑴.所謂幅角條件(相角條件):
①.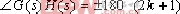 (k=0,1,2,3,……) (4-1) (k=0,1,2,3,……) (4-1)
②. 幅角條件是繪制根跡的根本依據
--根平面上凡是滿足幅角條件的點的全體就是根跡。
③.可利用幅角條件畫根跡。
⑵.所謂幅值條件:
①.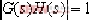 (4-2) (4-2)
②.根跡上凡是滿足幅值條件的點,就是相應K值的閉環極點sb,即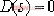 的根。 的根。
③.可利用幅值條件確定相應于sb的K。
⑶. 幅角條件與幅值條件不同點:
①幅角條件與K無關。
②.據幅值條件可知,幅值改變,相應于K在改變。
⑷.例
仍以圖4-1所示的系統為例,用幅角條件來求 由0→+∞變化時根軌跡,并用幅值條件確定使閉環系統的一對共軛復數極點的阻尼比ξ等于0.707時的K值。
對于上述給定系統,其幅角條件為: 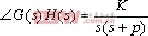
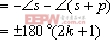 (k=0,1,2,3,……) (k=0,1,2,3,……)
其幅值條件為: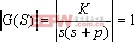
綜上可知,在作根軌跡圖時,只需應用幅角條件,即可畫出根的軌跡,然后利用幅值條件可求出根軌跡上某一點的相應的K值。因為在圖紙上繪制根軌跡的過程中,需要對幅角和幅值進行圖解測量,故必須將橫坐標軸與縱坐標軸按同樣的尺度進行等分。
⒉.繪制根軌跡步驟如下:
⑴.在S平面上畫出開環極點:
有兩個開環極點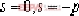 ,以×表示。 ,以×表示。
見圖4-4。
⑵.確定實軸上的根軌跡:
如果試驗點位于正實軸上,則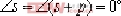 這表明不滿足幅角條件。因此,在正實軸上沒有根軌跡。 若將試驗點選在負實軸上, 這表明不滿足幅角條件。因此,在正實軸上沒有根軌跡。 若將試驗點選在負實軸上,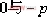 之間。 之間。
這時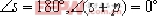 因此 因此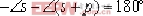
即滿足幅角條件。 因此, 在負實軸上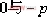 之間這一段是根軌跡一部分。 之間這一段是根軌跡一部分。 如果把試驗點選在負實軸上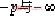 之間。這時 之間。這時 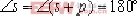 此顯然不滿足幅角條件。故在負實軸上從 此顯然不滿足幅角條件。故在負實軸上從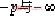 之間這一段,不是根軌跡一部分。 之間這一段,不是根軌跡一部分。
綜上,實軸上的根軌跡,存在于負實軸上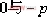 之間。 之間。
⑶.確定S平面上,除了實軸以外的其它根軌跡:
在S平面上任取一點 (見圖4-4),令╱s =Λ1, ╱s+p =Λ2 。如果 位于根軌跡上,則應滿足幅角條件,即Λ1+Λ2=180L。顯然,只有位于坐標原點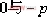 之間線段的垂直平分線上的點,才能滿足幅角條件,因此S平面上,該垂直平分線也是根軌跡的一部分。 之間線段的垂直平分線上的點,才能滿足幅角條件,因此S平面上,該垂直平分線也是根軌跡的一部分。
綜上所述,根據幅角條件求得并畫出當K由0→+∞變化時根軌跡與圖 4-2按公式直接計算根的值所畫出的根軌跡是完全一樣的,且前者不受系統方程階次的限制,明顯優于后者。
⑷.確定一對阻尼比ξ為0.707的共軛復數閉環極點:
這對閉環極點,位于通過原點且與負實軸夾角為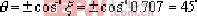 的直線上.由圖可以求出,當ξ=0.707時, 這一對閉環極點為 的直線上.由圖可以求出,當ξ=0.707時, 這一對閉環極點為
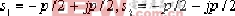
與這對極點相應的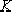 值,可用幅值條件確定為 值,可用幅值條件確定為![]()
技術專區
|
評論