4.7.1 正反饋回路根軌跡 ⒈引言:
前面介紹的繪制根跡的依據、法則,都是針對負反饋系統的。對于正反饋,前面的依據、規則,需要作些修改,修改以后的規則,可被用來畫正反饋回路的根跡。
⒉修改內容:
⑴.作圖依據:
①.特征方程: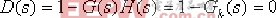 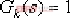
②.幅角條件: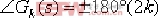 故稱零度根軌跡。 故稱零度根軌跡。
③.幅值條件: 和前面一樣。 和前面一樣。
⑵.作圖規則:
①.實軸上根跡:為所在線段的右面有偶數個開環零、極點。
②.(n-m)條漸近線傾角: k=0,1,2 k=0,1,2
③.根跡的出射角、入射角:
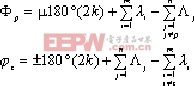
⒊結論: 按零度根軌跡規則,繪制正反饋回路根軌跡,其步驟同負反饋。下面舉例說明。
例4-6 設一反饋系統內回路為正反饋,如圖4-20所示,其開環傳遞函數為:
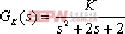
試繪制其內回路根軌跡。 圖4-20 ⑴.常規方法 ①.兩條根跡分支:分別起始于兩個開環極點-1+j, -1-j,終止于s平面∞處。 ②.實軸上根跡:因為實軸無開環零、極點,所以整條實軸是根跡。 ③.兩條漸近線之傾角: 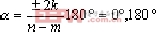 ④.開環極點-1+j的出射角: 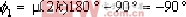 ⑤.會合點:由公式  ⑥.復平面上的根跡: 由幅角條件可知,兩個開環極點之間的連線是根跡。 ⑦.所求根跡,如圖4-21所示。 ⑵. “MATLAB”方法 解本題的MATLAB程序exe46.m: n=[-1];
d=[1 2 2];
rlocus(n,d)
title(‘4-21’) 執行本程序,可得正反饋根軌跡圖4-21 4.7.2 非最小相位系統之根跡
所謂非最小相位系統:
如果系統的所有極點和零點均位于s左半平面,則系統稱為最小相位系統。如果系統至少有一個極點或零點位于s右半平面,則系統稱為非最小相位系統。對于非最小相位系統之根跡繪制,要注意其幅角條件的變化。 例4-7 狀態空間模型的概念說明 設一非最小相位系統如圖4-22所示,試作出其根跡。 ⑴.常規方法 本系統的幅角條件為: 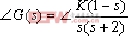 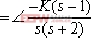 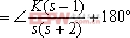
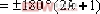 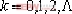
即 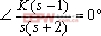
據上面方程可以作出如圖4-23所示
根軌跡。 ⑵.“MATLAB”方法 解本題的MATLAB程序exe47.m: n=[-1 1];
d=[1 2 0];
rlocus(n,d)
title(‘4-23’) 執行本程序,可得非最小相位系統根軌跡,如圖4-23所示。 ⑶.附言: 從這個系統的根軌跡圖,可以看出當根增益 小于2時,系統是穩定的。 |
評論