聲發射源多傳感器數據融合識別技術
2.1基于D-S理論的聲發射源識別方法[3]
從聲發射源發出的信號經過傳輸介質到達傳感器,信號會發生變化或損失,各個傳感器檢測到的波形信號一般是不完整、不精確、模糊的,甚至可能是矛盾的,即包含著過程的不確定性。我們只能根據這些不確定性信息進行分析推理,最終得出聲發射源的定性判別。不確定性推理最常用的方法有:Bayes方法和D-S證據理論兩種。與Bayes方法相比,D-S證據理論有一個非常突出的優點,就是無需先驗概率和條件概率,這對聲發射檢測這類幾乎沒有先驗知識和專家庫的新型技術顯得非常有用,而且各個傳感器之間的證據是相互獨立的,每個定位組的探頭數一般為三、四個,推理鏈不長,使用D-S規則非常方便。
對于聲發射源識別的數據融合模型結構按數據抽象的層次劃分主要有三類:數據級融合,特征級融合和決策級融合。根據聲發射信號的特點,一般選擇最高層次的融合方法,即決策級融合。由于球罐、橋梁等大型構件,通常采用數十個通道同時進行信號采集,而且一般聲發射檢測持續的時間較長,當進行全波形采集時數據量非常大,要對所有定位相關組的傳感器進行集中決策處理會大大降低系統的效率和實時性。所以,在各個傳感器局部目標識別的基礎上,進行全局決策的結構比較適合聲發射檢測的特點,操作起來非常靈活,也有利于減少系統的復雜程度,使整個決策系統清晰可靠。在一個或幾個傳感器判斷失效的情況下仍能繼續工作,即系統具有一定的容錯能力,總能得到一個唯一的識別結果。這對保證工程檢測結果能夠得到一個最終的安全性評價十分必要。此外,在工程上對于同一個聲發射源還可能進行其他檢測方法的復驗(如采用超聲、射線檢測等),以保證最終結果可靠。采用這種決策級的融合結構可以方便地對不同類型傳感器或者檢測方法的局部識別結果進行擴充融合,而不必對已有的系統結構做過多的修改。
應用D-S證據理論的關鍵是如何構造基本概率分布函數。D-S理論本身并沒有現成的表達式,使用者應根據經驗或具體的統計證據構造。對聲發射檢測的具體情況,構造如下概率分布函數[4]。
設N為同一定位組中傳感器的數目(對于三角形定位N=3),M為聲發射源的種類數(如裂紋、泄漏、外部噪聲等等),則
i=1,2,…,N (1)
j=1,2,…,M (2)
上式中各符號如下定義:
Ci(j):傳感器i與聲發射源類別j之間的屬性測度,是單個傳感器的識別結果。一般通過小波及神經網絡的處理獲得屬性測度值;



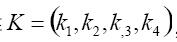
評論