基于FPGA的數字水印實現
The realization of digital watermarking based on FPGA
本文引用地址:http://www.j9360.com/article/201903/399042.htm程前 1 ,董長旭 1 ,廖媛媛 2
(1.電子科學與工程學院,四川 成都 610000;
2.電子科技大學,通信抗干擾技術國家級重點實驗室,四川 成都 610000)
摘要:數字水印技術在信息安全、知識產權保護和認證等領域有著重要的功能和地位。本文基于現場可編程門陣列(FPGA),通過流水線設計,乒乓緩沖和分布式算法,實現8×8矩陣的二維DCT變換,充分利用FPGA的查找表(LUT)和塊RAM(BRAM)資源,實現載體圖像的快速DCT域變換。原始水印圖像通過Arnold變換進行置亂,并與Logistic映射的混沌序列選擇合適的水印信息嵌入點。最后通過不同的水印攻擊來驗證本系統的
隱蔽性和魯棒性。
關鍵詞:水印圖像;二維DCT;分布式算法;Arnold置亂;混沌序列
0 引言
隨著通信技術的飛速發展,數字媒體通信在信息交流中得到了廣泛的應用。網絡信息交換之間的安全和加密等問題引起了高度重視[1],保證信息不被非法利用和破壞也變得越來越重要。圖像數據可承載比文字更多的內容,成為信息傳遞的重要途徑。傳統的加密方法主要針對數據傳輸過程進行保護,而不能完全解決接收解密后的安全性問題,而利用信息隱藏技術通過在公開的載體信息中插入隱藏的機密信息后進行數據傳輸,實現了信息的安全隱秘傳輸[2]。
數字水印技術可以廣泛用于信息安全、知識產權保護和認證等領域,其通過某一種水印算法,實現將包含機密信息的水印圖像隱藏在傳輸的載體圖像中,而數據接收方則通過專用解密方法提取水印信息,實現圖像數據安全提取和傳輸[3]。
1 圖像水印實現系統整體方案
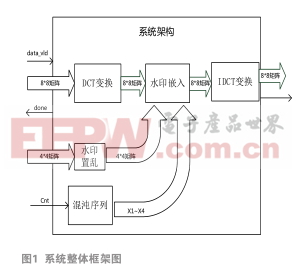
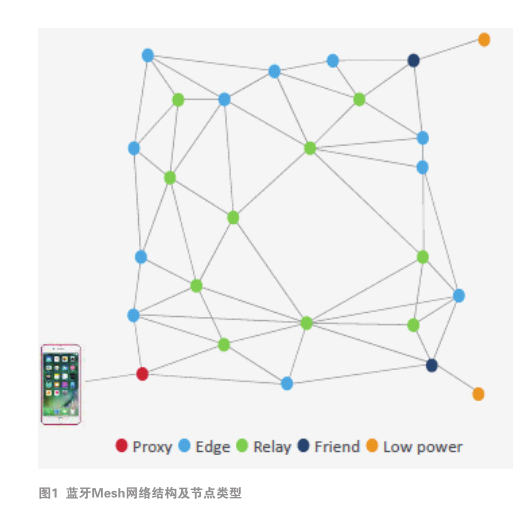
本系統分為水印嵌入和水印提取兩個模塊,實現將水印圖像嵌入載體圖像后提取加密水印,整體框架圖如圖1所示。
2 水印嵌入模塊
水印嵌入模塊選擇在空間域或變換域進行水印圖像嵌入載體圖像。首先將200×200的二值水印圖像進行置亂處理后,利用混沌序列在800×800載體圖像中選擇合適的水印嵌入位置,在制定的嵌入規則指導下進行水印的嵌入。本系統的水印嵌入模塊主要包括DCT變換模塊、Arnold置亂模塊、混沌序列模塊等。
2.1.1 二維DCT變換模塊
最初的數字水印算法是基于空間域實現,是在嵌入規則下直接實現水印圖像嵌入。雖然空間域嵌入可實現高速變換并降低系統復雜度,但是難以實現較好的魯棒性和不可感知性。變換域是指通過某一算法,常見的包括離散余弦變換(DCT),離散傅里葉變換(DFT),離散小波變換(DWT)等,將載體圖像變換到頻域進行水印圖像的嵌入,這樣可實現高魯棒性,高安全性的水印不可感知嵌入系統。因為DCT變化是圖片JPEG壓縮標準,所以本系統選擇在DCT域進行水印嵌入,實現高抗JPEG壓縮攻擊性[4]。
本 系 統 選 擇 對 8 0 0 × 8 0 0 的 載 體 圖 像 進 行8 × 8 矩 陣 分 塊 后 , 形 成 x(i,j) 0 ≤ i < 8, 0 ≤ j < 8的矩陣數據,然后再經過二維DCT得到變換結果X(m,n) 0 ≤ m < 8, 0 ≤ n < 8 ,二維DCT的公式如下:
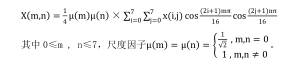
其中0≤m , n≤7,尺度因子。
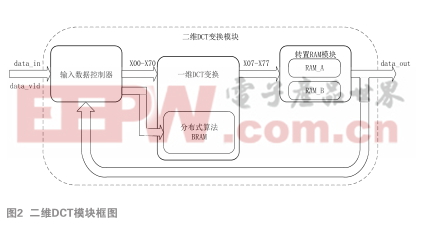
二維DCT運算算法十分復雜,若用組合邏輯實現將大大影響系統的時序性能,本系統利用其可分解性質,對8×8矩陣每行首先進行一維DCT變化,然后對變換結果每列進行一維DCT即可得到二維DCT變換結果,具體操作步驟如下:一維DCT變換公式可以表示為矩陣形式:對于二維DCT變換,其公式可以用矩陣表示為:更進一步,可以將二維DCT變換分解:為了得到更快的工作頻率,本系統選擇通過流水線設計改善其時序性能,提高計算效率。緩存時加入乒乓操作改善輸入速度和輸出速度差距過大的問題,巧妙設計時序增加資源利用率。由于dct模塊和轉置ram只例化一次,實現最小資源耗費。一維DCT算法基本操作即為8×8矩陣相乘,需要大量的乘累加運算,占用FPGA的專用乘法器資源,所以為了實現資源優化,本系統通過分布式算法,將一維DCT的系數矩陣C 8×8 與輸入數據可能的運算結果事先存儲在FPGA的BRAM資源中,利用真正的輸入行/列數據產生地址進行讀操作即可正確實現一維DCT運算。最終本系統實現100個周期內完成一次完整的兩個8×8矩陣的DCT變換(IDCT同理)。
2.1.2 Arnold置亂模塊
水印圖像的置亂操作,簡單來說就是將所有像素按照一定規則實現重新排序,使得圖像成為雜亂的不可識別圖像,從而隱藏水印信息,本質上就是對水印圖像的加密 [5] 。置亂后的水印圖像可以降低噪聲或者攻擊的影響,提高水印信息的魯棒性和抗攻擊性。本系統采用Arnold置亂對水印圖像進行處理,通過FPGA將32位200×200的原始水印圖像進行置亂。模塊將水印信息原存儲地址經過置亂后,得到Arnold存儲器地址后將水印信息重新存入。
地址變換是將水印圖像原地址(x,y)處的像素點移動至變換后的位置(x’,y’),其中位置變換公式為:x’ = (x + y) / 200,y’ = (x + 2y) / 200。

同時Arnold置亂具有周期性,通過仿真發現圖像的置亂周期為150,即經過150次置亂后得到原圖像,所以在水印嵌入模塊進行N Arnold 次置亂后,在水印提取模塊進行150-N Arnold 次置亂即可恢復水印圖像。
本系統的Arnold置亂模塊利用上述公式,對水印圖片的行/列地址進行置亂。首先將輸入的水印圖像信息按行的順序串行輸入并進行N Arnold 次Arnold置亂,利用遞減循環操作進行置亂地址的200減法求余運算,最終得到完成Arnold置亂的水印圖像,圖3的原始水印圖像經過90次Arnold置亂后得到圖4所示的置亂水印圖像。
2.1.2 混沌序列模塊
混沌現象非周期,不收斂,有界且對初值敏感,是非線性動態系統中出現的確定的類似隨機過程,可以容易地生成很多非相關、類隨機的確定再生信號。
映射是廣泛應用于混沌系統中的一個非線性方程 [6] ,公式如下:其 中 x, μ 是 分 支 系 數 , 且3.5699456≤μ≤4時,Logistic映射工作于混沌狀態,本系統選擇μ=3.875,初始值x 0 =0.621,在基于FPGA設計系統時,應盡可能避免小數操作,所以將μ右移3位得到U=31,初始值x 0 右移8位得到x 0 =159。輸入初值進行Logistic映射時,按照x i+1 =U×X i (1-X i )運算,得到的值x i+1 左移11位即可得到0~1之間的混沌序列。


(1)嵌入規則
本系統設計為盲水印算法,即在水印檢測過程中時,只需要密鑰而不需要原始數據的參與。在水印嵌入過程中,引入了混沌序列作為水印嵌入點選擇的條件。
由于混沌序列本身具有初值敏感性特性(即初值不同產生的序列完全不同),因此,引入混沌序列作為密鑰將進一步提高算法的隱蔽性。
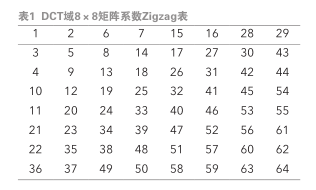
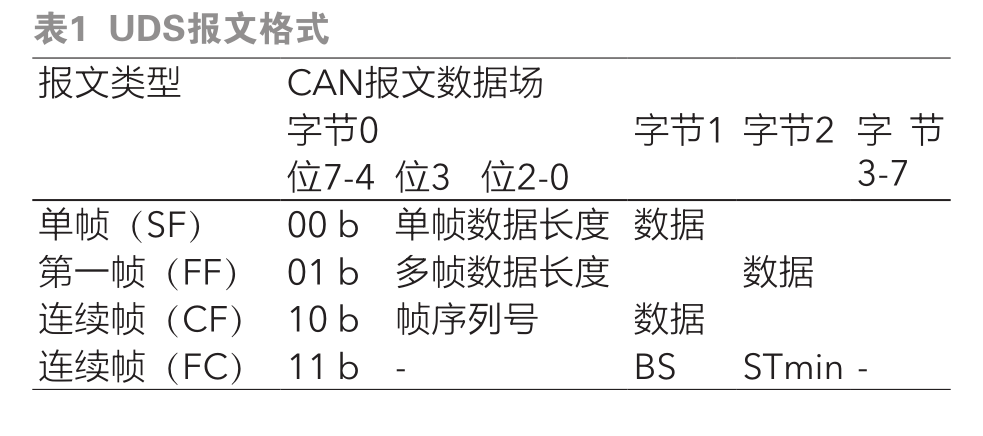
DCT 域8×8矩陣中的頻域系數進行編號得到順序排列表,且表從左上角到右下角代表著從圖像的低頻部分到高頻部分,如下表1所示。
根據 Waston 模型的頻率敏感度特性,同時考慮圖像進行JPEG壓縮后圖像質量不出現明顯降低,本系統選擇在中頻系數選擇合適的像素點,基于加法水印嵌入規則將200×200的水印圖像嵌入800×800的載體圖像,即可劃分為將4個水印圖像信息嵌入8×8載體圖像矩陣中,同時基于嵌入規則在可選4個像素點中選擇嵌入1個水印信息,嵌入比為1/16,因此為了嵌入所有水印信息,需要在8×8的載體圖像矩陣中選擇4組16個像素點。綜合考慮,本文選擇Zigzag 表中編號為19、20和 8、10 ,9、11和12、14 , 13、15和17、21 , 16、18和22、23這4組像素點進行水印圖像嵌入。最后根據上述置亂后的水印信息W,混沌序列值為X,每組像素點的系數分別為F1,F2,F3,F4,最終選擇一個合適的a值實現加法嵌入規則得到最終的像素點F0:
如果 X = 1,W = 1:若 F4 < F3,則F0 = F3+a,否則F0 = F4+a;
如果 X = 1,W = 0:若 F4 > F3,則F0 = F3- a,否則F0 = F4 -a;
如果 X = 0,W = 1:若 F2 < F1,則F0 = F1+a,否則F0 = F2+a;
如果 X = 0,W = 0:若 F2 > F1,則F0 = F1- a,否則F0 = F2-a。

(2)系統運行結果
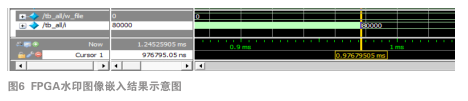
將800×800載體圖像和200×200的水印圖像轉化成二值數據傳入本系統,仿真結果如圖5(a)(b)
(c)(d)所示,可以發現嵌入水印后的圖像與載體圖像并沒有視覺上的失真,具有良好的水印不可見性,同時在未受攻擊時,水印圖像具有很好的隱蔽性。
對嵌入水印后的載體圖像分別進行1/4裁剪攻擊,方差 0.01的高斯加噪攻擊和馬賽克攻擊后提取水印信息來驗證本系統的魯棒性,攻擊方法如圖4(e)(g)(i)所示,結果如圖4(f)(h)(j)
所示,可以發現經過三種水印攻擊后,本系統仍舊可以提取水印信息,且通過仿真知,抵抗剪裁攻擊后的相關系數NC=0.7464,抵抗高斯噪聲后的相關系數NC=0.9998,抵抗馬賽克攻擊后的相關系數。
3.2 硬件速度與資源使用情況
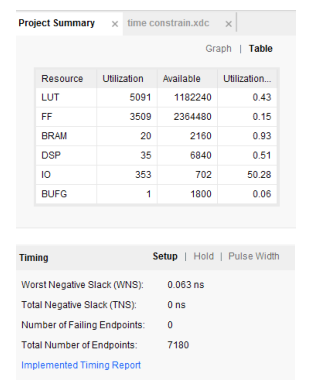
通過仿真圖5(a)可以發現,本系統在經過時序優化后,完成一次圖片處理小于1 ms,可在頻率下正常工作,并實現100 ms內完成100個水印圖像嵌入操作。FPGA硬件使用資源如圖5(b)所示,除IO接口外使用的資源不足FPGA開發板資源的1%。
4 結論
本系統在全國大學生集成電路創新創業大賽中,適用于參賽題目“華為云杯-圖片水印實現”,最終獲得西南分賽區一等獎,全國總決賽三等獎。本系統將繼續在架構上對二維DCT變換模塊進行優化,在保證功能的同時,降低FPGA的IO接口資源使用率。
參考文獻:
[1] 李趙紅, 侯建軍. 基于Logistic混沌映射的DCT域脆弱數字水印算法[J]. 電子學報, 2006,34(12):2134-2137.
[2] 于平平. 基于VLSI實現的數字圖像水印技術研究[D]. 天津大學, 2010.
[3] 常曄. 基于DCT域的圖像數字盲水印算法設計及硬件實現[D]. 天津大學,2010.
[4] 張釘銘. 基于FPGA的數字水印算法實現[D]. 南京航空航天大學, 2012.
[5] 倪蓉蓉, 阮秋琦. 利用Arnold對稱性變換的圖像信息隱藏算法[J]. 北京交通大學學報, 2002, 26(2):25-28.
[6] 劉昕浩, 郭騰, 謝德輝,等. 基于Logistic混沌映射的圖像加密通信系統研究[J].湖南理工學院學報(自科版), 2015, 28(4):27-31.
本文來源于科技期刊《電子產品世界》2019年第4期第76頁,歡迎您寫論文時引用,并注明出處



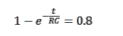
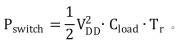

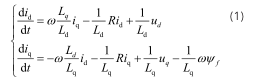
評論