本文作者maxfiner，畢業于西安電子科技大學，擁有信號與信息處理專業碩士學位。maxfiner曾供職于華為通信技 術公司無線通信部門，擁有多年的工程項目研發經驗，同時兼備算法理論研究，仿真驗證，以及對應的硬件設計實現能力；具備通信物理層開發設計各個方面的實戰 經驗...

　　從事信號處理相關工作，不可避免的用到一些數學知識。通常來說，用到啥，就回頭去看啥，或者說，缺啥補啥。有一些數學知識，是頻繁和反復用到的，因此有必要把它們匯總下。數學方面的東西，只看數學書籍的話，一般情況下，是相當乏味和枯燥的，但是和實際應用結合起來，就發現數學的魅力、力量和威力還是很強大的。和實際問題結合起來，數學也就變得有趣起來。在這里，暫時舉出三例，后續繼續豐富和完善。

　　一 復數的概念

　　復數可以說是我們從小到大一路走來，最后學到的一種數了。從歷史的角度看，它也是最后引入的幾個數之一，直到最近幾百年才開始引入并推廣應用。它是為了解方程的方便而引入的，而且一開始還一直不被人們接受，這些人中包括很多大數學家。可見一個新的事物，一個新的概念，一種新的思想，要想被人接受是很困難的，很漫長的一件事情。但是，隨著時間的發展，由于它的獨特價值，最終被人接受并廣泛應用。復數除了解方程之外，在工程領域，最能體現復數應用價值的是兩個方向，一個是量子力學，一個就是電磁學。

　　復數的概念在電子工程，電磁場與電磁波等領域應用極為廣泛，在信號處理方向更是如此。不論是信號處理的基礎理論——傅里葉變換，還是信號的基帶表示和帶通表示，解析表示，不論是頻譜的分析，還是討論信號的時移和相位，都離不開復數這個有力的工具的支撐。

　　相關概念：

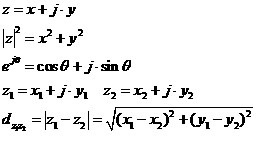
　　應用舉例簡述如下，在相關章節會分別進行更詳細的介紹。

　　BPSK，QPSK，16QAM等調制方式，信號星座可看做信號正交分量和同相分量的復數域的表示。

　　發射機的EVM測試，即根據星座點在復平面上的位置進行計算，計算的目標就是實際測得的星座點和參考星座點之間的距離，或者說就是復平面上兩個點的距離。

　　接收機存在某個頻率偏移時，星座圖上的星座點會以恒定速率旋轉，圍繞原點做勻速圓周運動，運動角速度和頻率偏移大小成正比。

　　電路的阻抗分析、諧振分析均以復數運算為基礎。

　　實信號的頻譜是共軛對稱的。頻譜的鏡像可用共軛成分來表示。

　　安捷倫和羅德施瓦茨都有矢量信號發生器，矢量信號分析儀，這些信號都是復數形式的信號。

　　信道估計算法，本質上可以看做是復數的除法運算。

　　發射機的正交上變頻，接收機的正交下變頻，本質上可以看做復數的乘法運算。

　　接收機頻偏的補償，本質上可以看做復數的乘法運算。

　　發射機鏈路和接收機鏈路上各個節點的功率的計算，為復數的模平方的計算，在信號功率監測，模擬自動增益控制（AAGC），數字自動增益控制（DAGC）等領域中有廣泛應用。

　　二 信號的伸縮和平移

　　信號的伸縮和平移，尤其是平移，在信號處理的理論和實踐中有著廣泛的應用。信號時域的平移和頻域的相移之間的關系，是非常奇妙而又應用廣泛的一對關系。信號的伸縮和平移，從數學上來說，就是函數的伸縮和平移的應用，這是高中初等數學的范疇，應該是非常一般的，即使很久不用數學也不會忘記的一個概念和方法。但是因為它如此的重要，因此有必要單獨拿出來進行一個小小的總結，從而更好的利用這一有效工具去解決各種信號處理相關的問題。這一章節專門討論和總結平移。伸縮的討論等到真正用到它時（比如信號的插值和抽取）再進行相應描述。

　　信號的平移，最簡單的是記住四個字——“加左減右”。即移動量是正值，則整個信號波形向左移動，即向x坐標軸的負軸方向移動。移動量是負值，則整個信號波形向右移動，即向x坐標軸的正軸方向移動。雖然想象左右比想象上下的心理反應時間要慢些，但多多體會就會熟記于心的。

　　舉個例子，比如單位采樣信號為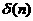不妨想一下，和單位沖擊信號有何區別呢？），如下圖所示：

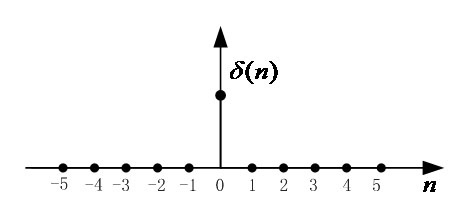
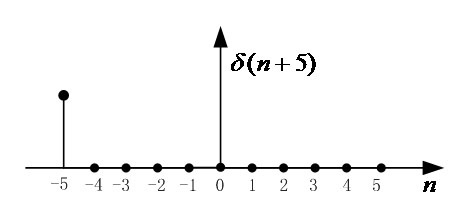
　　若是信號形式為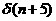則整個波形向左移動5個采樣點，如下圖所示：

　　對于一般的一個信號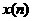可以根據單位采樣信號的平移性質，表示成如下形式：

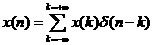
　　也就是說，任何一個離散信號，都可以表示成單位采樣信號的線性疊加形式。從信號與系統的角度來說，這是系統線性疊加的體現。這里的系統，當然是線性時不變系統，滿足齊次性，疊加性和時不變性，這是我們所有關于信號與系統的分析的前提。

　　三 和差化積公式

　　積化和差公式最普遍、最頻繁的應用就是信號的上下變頻處理。后續我們結合信號的基帶表示和帶通表示的時候會進行更細致的描述。

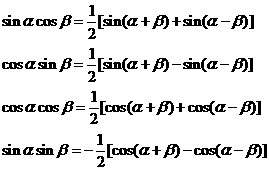
　　若是一下子記不住這四個公式，可以先理解第三個，然后依次類推。雖然說數學需要理解，但是實踐證明，為了更好和更高效的應用，一些極其常用的概念和公式還是記牢的好。

　　比如諸如積化和差之類的三角公式，比如香農公式，比如2的N次方（2N16）。

下期開講——精通信號處理設計小TIps（6）：卷積是怎么得到的？敬請關注！

聲明：電子發燒友網版權所有，謝絕轉載！