單片機主要作用是控制外圍的器件，并實現一定的通信和數據處理。但在某些特定場合，不可避免地要用到數學運算，盡管單片機并不擅長實現算法和進行復雜的運算。下面主要是介紹如何用單片機實現數字濾波。

　　在單片機進行數據采集時，會遇到數據的隨機誤差，隨機誤差是由隨機干擾引起的，其特點是在相同條件下測量同一量時，其大小和符號會現無規(guī)則的變化而無法預測，但多次測量的結果符合統計規(guī)律。為克服隨機干擾引起的誤差，硬件上可采用濾波技術，軟件上可采用軟件算法實現數字濾波。濾波算法往往是系統測控算法的一個重要組成部分，實時性很強。

　　采用數字濾波算法克服隨機干擾的誤差具有以下優(yōu)點：

　　l 數字濾波無需其他的硬件成本，只用一個計算過程，可靠性高，不存在阻抗匹配問題。尤其是數字濾波可以對頻率很低的信號進行濾波，這是模擬濾波器做不到的。

　　l 數字濾波使用軟件算法實現，多輸入通道可共用一個濾波程序，降低系統開支。

　　l 只要適當改變?yōu)V波器的濾波程序或運算，就能方便地改變其濾波特性，這對于濾除低頻干擾和隨機信號會有較大的效果。

　　l 在單片機系統中常用的濾波算法有限幅濾波法、中值濾波法、算術平均濾波法、加權平均濾波法、滑動平均濾波等。

　　（1）限幅濾波算法

　　該運算的過程中將兩次相鄰的采樣相減，求出其增量，然后將增量的絕對值，與兩次采樣允許的最大差值A進行比較。A的大小由被測對象的具體情況而定，如果小于或等于允許的最大差值，則本次采樣有效；否則取上次采樣值作為本次數據的樣本。

　　算法的程序代碼如下：

　　#define A //允許的最大差值

　　char data; //上一次的數據

　　char filter（）

　　{

　　char datanew; //新數據變量

　　datanew=get_data（）; //獲得新數據變量

　　if（ （datanew-data）》A||（data-datanew》A） ）

　　return data;

　　else

　　return datanew;

　　}

　　說明：限幅濾波法主要用于處理變化較為緩慢的數據，如溫度、物體的位置等。使用時，關鍵要選取合適的門限制A。通常這可由經驗數據獲得，必要時可通過實驗得到。

　　（2）中值濾波算法

　　該運算的過程是對某一參數連續(xù)采樣N次（N一般為奇數），然后把N次采樣的值按從小到大排列，再取中間值作為本次采樣值，整個過程實際上是一個序列排序的過程。

　　算法的程序代碼如下：

　　#define N 11 //定義獲得的數據個數

　　char filter（）

　　{

　　char value_buff［N］; //定義存儲數據的數組

　　char count，i，j，temp;

　　for（count=0;count《N;count++） //獲取數據

　　{

　　value_buf［count］=get_data（）;

　　delay（）; //如果采集數據比較慢，那么就需要延時或中斷

　　}

　　for（j=0;j《N-1;j++） //用冒泡法對數據進行排序，當然最好用其他排序方法

　　{

　　for（value_buff［i］》value_buff［i+1］

　　{

　　temp=value_buff［i］;

　　value_buff［i］=value_buff［i+1］;

　　value_buff［i+1］=temp;

　　}

　　}

　　return value_buff［（N-1）/2］;

　　}

　　說明：中值濾波比較適用于去掉由偶然因素引起的波動和采樣器不穩(wěn)定而引起的脈動干擾。若被測量值變化比較慢，采用中值濾波法效果會比較好，但如果數據變化比較快，則不宜采用此方法。

　　（3）算術平均濾波算法

　　該算法的基本原理很簡單，就是連續(xù)取N次采樣值后進行算術平均。

　　算法的程序代碼如下：

　　char filter（）

　　{

　　int sum=0;

　　for （count=0;count《N;count++）

　　{

　　sum+=get_data（）;

　　delay（）：

　　}

　　return （char）（sum/N）;

　　}

　　說明：算術平均濾波算法適用于對具有隨機干擾的信號進行濾波。這種信號的特點是有一個平均值，信號在某一數值附近上下波動。信號的平均平滑程度完全到決于N值。當N較大時，平滑度高，靈敏度低；當N較小時，平滑度低，但靈敏度高。為了方便求平均值，N一般取4、8、16、32之類的2的整數冪，以便在程序中用移位操作來代替除法。

　　（4）加權平均濾波算法

　　由于前面所說的“算術平均濾波算法”存在平滑度和靈敏度之間的矛盾。為了協調平滑度和靈敏度之間的關系，可采用加權平均濾波。它的原理是對連續(xù)N次采樣值分別乘上不同的加權系數之后再求累加，加權系數一般先小后大，以突出后面若干采樣的效果，加強系統對參數變化趨勢的認識。各個加權系數均小于1的小數，且滿足總和等于1的結束條件。這樣加權運算之后的累加和即為有效采樣值。其中加權平均數字濾波的數學模型是：

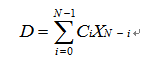
　　式中：D為N個采樣值的加權平均值：XN-i為第N-i次采樣值；N為采樣次數；Ci為加權系數。加權系數Ci體現了各種采樣值在平均值中所占的比例。一般來說采樣次數越靠后，取的比例越大，這樣可增加新采樣在平均值中所占的比重。加權平均值濾波法可突出一部分信號抵制另一部分信號，以提高采樣值變化的靈敏度。

　　樣例程序代碼如下：

　　char code jq［N］={1，2，3，4，5，6，7，8，9，10，11，12}; //code數組為加權系數表，存在程序存儲區(qū)

　　char code sum_jq=1+2+3+4+5+6+7+8+9+10+11+12;

　　char filter（）

　　{

　　char count;

　　char value_buff［N］;

　　int sum=0;

　　for（count=0;count《N;count++）

　　{

　　value_buff［count］=get_data（）;

　　delay（）;

　　}

　　for（count=0;count《N;count++）

　　sum+=value_buff［count］*jq［count］;

　　return （char）（sum/sum_jq）;

　　}

　　（5）滑動平均濾波算法

　　以上介紹和各種平均濾波算法有一個共同點，即每獲取一個有效采樣值必須連續(xù)進行若干次采樣，當采速度慢時，系統的實時得不到保證。這里介紹的滑動平均濾波算法只采樣一次，將一次采樣值和過去的若干次采樣值一起求平均，得到的有效采樣值即可投入使用。如果取N個采樣值求平均，存儲區(qū)中必須開辟N個數據的暫存區(qū)。每新采集一個數據便存入暫存區(qū)中，同時去掉一個最老數據，保存這N個數據始終是最新更新的數據。采用環(huán)型隊列結構可以方便地實現這種數據存放方式。

　　程序代碼如下：

　　char value_buff［N］;

　　char i=0;

　　char filter（）

　　{

　　char count;

　　int sum=0;

　　value_buff［i++］=get_data（）;

　　if（i==N）

　　i=0;

　　for（count=0;count《N;count++）

　　sum=value_buff［count］;

　　return （char）（sum/N）;

　　}

　　今天就寫到這，因為數字濾波的算法還有很多種方法，比如一階滯后低通濾波器（慣性濾波法），限時濾波，容錯冗余三中取二濾波法等等。不過由于個人能力和時間的原因，還沒能把它們一一地列出。以后我會不斷地找資料把它們完善。