連續時間Σ-Δ調制器(Continuous-Time ΔΣ Modulator)先天上具有對輸入信號濾波的效果，可降低前級濾波器設計復雜度，并提升信號質量，因而成為現今無線通信系統接收機(Receiver)設計的常用方案。

無線技術目前已廣泛應用于人類的生活中，低功率無線收發器(Ultra-Low-Power Wireless Transceiver)更是無線通信電路發展的重要關鍵。目前接收(Receiver)中的模擬數字轉換器(ADC)普遍提出的架構，皆以低通Σ-Δ調制器(Low-pass Delta-Sigma Modulator)為主(圖1)，信號經過帶通濾波器(BPF)、低噪聲放大器(LNA)，再經由混頻器(Mixer)做降頻的動作，接著在基帶(Baseband)做數字化處理。

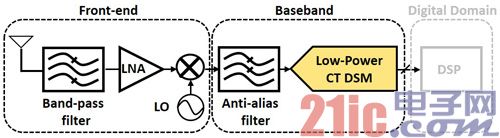
圖1 傳統接收器架構圖

Σ-Δ模擬數字轉換器(Delta-Sigma Analog-to-Digital Converter)一直以來是一個可以得到高分辨率(Resolution)的電路架構，其中連續時間Σ-Δ調制器(Continuous-Time Delta-Sigma Modulator, CTDSM)因先天上具有對輸入信號濾波的效果，使前級濾波器在設計需求上可以比較寬松，因此CTDSM成為在設計接收機時，常被使用的要素之一。當然此類的ADC設計上有許多地方須要注意，現今仍有諸多文獻在這個領域有不少著墨，以致力于低功耗、寬帶的CTDSM設計。

本文主要分成兩大部分，第一部分為過采樣ADC的基本運作原理介紹，第二部分則針對現今文獻在CTDSM所提出的技術，做一些簡單的介紹。

采樣/量化影響ADC信號準確

ADC的運作過程主要分為采樣(Sampling)和量化(Quantization)兩大步驟。采樣的動作是將連續信號轉為離散的數據，在此過程中，勢必會遇到兩個問題，第一是如何確定取得的結果為所需要的信號;第二是要多快的采樣頻率才夠準確。

由頻率圖(圖2)的結果可以發現，第一，為了確保采樣信號確實是我們要的，一般會先經過抗混疊濾波器(Anti-Alias Filter)來過濾不要的信號;第二，經過采樣后，若信號帶寬超過fs/2的話，那數據會互相重迭導致失真發生，如同尼奎斯特準則(Nyqusit-Sample-Theorem)中所述，采樣頻率至少必須大于兩倍數據帶寬。

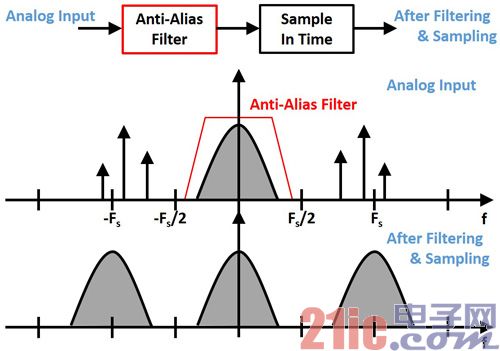
圖2 采樣頻譜圖

量化的動作是將連續的振幅轉為離散數值，而量化中產生的誤差會影響準確度(圖3(a))，假設輸入的信號為一個三角波(Ramp Signal)，則量化誤差會呈現鋸齒波(圖3(b))，并分布在±0.5Δ內(表示Δ量化階的差值);如果輸入沒有造成超負荷(Overload)，則量化誤差可以視為一個均勻分布的函數，其機率密度函數ρ(e)如圖4所示，其平均值(Mean Value)為0，量化誤差的功率等于其變異值(Variance)，可表示為：

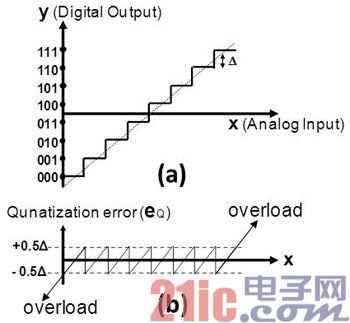
圖3 (a)3位的轉移函數、虛線為三角波輸入，(b)對應之量化誤差

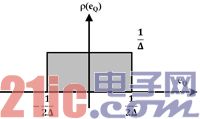
圖4 量化誤差的機率密度函數

......公式1

接著為了求ADC的信噪比(SNR)，必須要知道信號的功率。若輸入一個弦波到一個輸出為N個位的ADC，在轉換器未達超負荷的前提下，輸入弦波的最大振幅為A，則A滿足：

......公式2

所以輸入的功率可以表示為：

......公式3

因此SNR的最大值可以表示為：

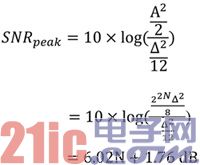
......公式4

根據上述公式，每增加一個位可以增加6dB，所以對于一個高分辨率的ADC，則實際上需要一個N位的輸出，這在實作上將難以達成，因此后來提出過采樣(Oversampling)的方式來改善這個問題。

搭配噪聲整形 過采樣可減少誤差

上述在ADC滿足采樣頻率為信號帶寬兩倍的，屬于尼奎斯特型(Nyquist Rate) ADC(圖5(a))。過采樣的意思即是采樣頻率大于兩倍的帶寬，這時候可以定義一個參數是過采樣比例(Over-Sampling-Ratio, OSR)為：

1)>

圖5 (a)量化誤差功率分布(OSR=1)，(b)量化誤差功率分布(OSR>1)

(FB為信號的帶寬)............................公式5

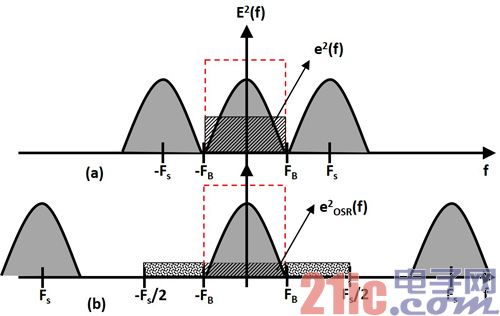
假設量化誤差為白噪聲(White Noise)，即它的功率為均勻地分布在Fs/2之間(圖6(b))，則它的功率譜密度(Power-Spectral-Density)為：

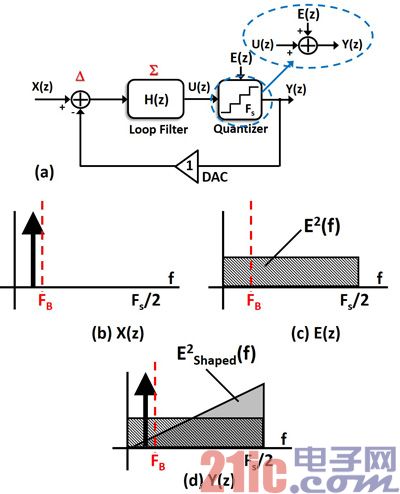
圖6 (a)三角積分器示意圖;(b)輸入X(z)頻譜圖;(c)量化誤差E(z)頻譜圖;(d)輸出Y(z)頻譜圖

......公式6

則于信號帶寬(FB)內的總量化誤差功率PNoise,OSR為：

......公式7

因此SNROSR的最大值可以表示為：

......公式8

由上述公式可以知道，固定信號帶寬下，每兩倍OSR(即Fs兩倍)僅增加3dB(0.5個位)。由結果可以發現，僅增加OSR所獲得的好處并不大，因此一般會進一步配合噪聲整形(Noise-Shaping)的技巧。

Σ-Δ調制器改善量化誤差

三角積分器本身即同時采用過采樣及噪聲整形兩項技巧，噪聲整形即利用相減(Delta, Δ)和積分(Sigma, Σ)組合而成(圖6(a))。則量化誤差E(z)所經過的轉移函數(Noise-Transfer-Function, NTF)為：

......公式9

則輸入信號X(z)所經過的轉移函數(Signal-Transfer-Function, STF)為：

.....公式10

由上面兩個公式可以發現，當選擇H(z)為一個高直流增益的低通濾波器時，噪聲轉移函數則為一個高通濾波器函數，代表本來為白噪聲分布的量化噪聲E(z)會經過高通濾波器塑型;而信號轉移函數則為一個低通濾波器函數，代表在低頻時，輸入信號X(z)經過增益為一的輸入轉移函數到輸出。而同時因為采用過采樣，所以信號帶寬相對于采樣頻率小很多，即大部分的量化誤差都被塑型到信號帶寬(FB)外面，所以帶寬內的量化誤差被大幅度的減少。

因此，調制器的輸出Y(z)包含輸入信號即經過塑型的量化誤差ESHAPE(z)(圖6(b)(c)(d))。最后依據環路濾波器(Loop-Filter)為離散型H(z)或連續型H(s)，可分為連續型或離散型Σ-Δ調制器。一個環路濾波器階數為L的Σ-Δ調制器，其SNRDSM的最大值可以表示為：

......公式11

由上面公式可以知道，固定信號帶寬下，每兩倍OSR可以增加(6L+3)dB，假設一個三階的環路濾波器，則可以增加21dB，相對于只有做過采樣，可多得到18dB(三個位)。

低功率CTDSM適用于無線通信系統

以下將針對連續型三角積分器中各個子區塊做說明。在過采樣Σ-Δ調制器中，架構上可以分成兩種形式，一種是離散時間Σ-Δ調制器(Discrete-time Delta-sigma Modulator, DTDSM)，另一種則是CTDSM。由于架構先天上的優勢，CTDSM比起DTDSM更適用于高速、寬帶的應用;但是隨著帶寬需求的增加，采樣頻率(Fs)也會隨著增加，伴隨而來的就是更高的功率消耗，主要可以分幾個部分來說明。

首先，因為帶寬的增加，使得用來實現CTDSM中環路濾波器的運算放大電路，需要更高的單位增益帶寬(Unit Gain Bandwidth)，這樣的需求也同時伴隨著更高的功率消耗;另一方面，因為用于CTDSM中的量化器，是操作在采樣頻率的速度，因此隨著采樣頻率的增加，也會使得量化器為了達到速度的需求，須要消耗更多的電流來壓低運算時間。

在高規格的CTDSM中，為了增加回授路徑上之數字模擬轉換器(Digital to Analog Converter, DAC)的線性度，常會使用數據加權平均(Data Weighted Averaging, DWA)的方法，來降低DAC中各個單位Cell之間不匹配所造成的Harmonic Tone。

再者，由于整個CTDSM是一個負反饋的閉回路系統，這使得每一筆從量化器輸出的數據，都需要在小于一個、甚至是半個采樣周期的時間回授到CTDSM的輸入，系統才會穩定，也就是整個信號路徑包含環路濾波器、量化器以及DWA所貢獻的延遲，須要壓在半個周期(0.5/Fs)內完成。

當環路濾波器以及量化器都會貢獻一定程度上的延遲時，DWA電路就須要操作在更高的速度，使其所貢獻的延遲更小，保持CTDSM系統的穩定，但是更高速的操作，就代表需要更多的功率消耗。

最后，就是延遲回路(Excess Loop Delay, ELD)的補償。因為整個閉回路系統上的電路所貢獻的延遲時間，相較于采樣頻率是不可忽略的，因此這樣額外的延遲等效上就是在系統上增加額外的極點，使得系統穩定度下降。

為了補償這個不理想性，高速的CTDSM通常需要額外的補償路徑，使系統可以正常的操作，而這個額外的補償路徑通常需要額外的DAC甚至是額外的運算放大器來實現信號相加減的運算，這都使得高速CTDSM比起低速的CTDSM，須消耗更多的硬件以及功耗。

但是，如果希望在CTDSM應用于無線通信系統中，功耗就必須壓低，基于這樣的需求，有許多技術被提出來降低CTDSM中各部分的功率消耗。

基本上CTDSM系統架構可以簡單分為幾個電路區塊，主要的電路區塊包含環路濾波器、DAC、量化器(Quantizer)和DWA(圖7)。

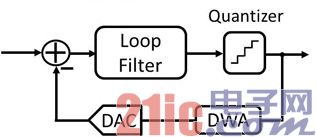
圖7 CTDSM基本架構

Gm-C/VCO/Twin-T降低環路濾波器功耗

通常在CTDSM中，如果希望壓低量化誤差，其中一個方法就是增加環路濾波器的階數，階數越高，對帶寬內量化誤差的壓抑效果就越好，但是伴隨而來的就是要采用更多的運算放大器來實現積分電路，以達到所需環路濾波器的方程式。

通常積分器的實現都是采用Active-RC架構，環路濾波器的階數多增加一階，就須要多增加一個Active-RC電路來實現積分電路;再者，用于Active-RC電路中的運算放大器是屬于閉回路應用(Active-RC中的C，通常連接于運算放大器的輸入與輸出，形成負回授)，所以此運算放大器的單位增益帶寬必需是采樣頻率的兩到三倍，系統才會穩定。

基于這個考慮，有些高速的應用，就會適當的引入Gm-C架構來實現積分電路，因為Gm-C電路中，Gm的實現是屬于開回路的實現方式(Gm的輸入與輸出點之間并無回授路徑)，因此對于用來實現Gm電路的單位增益帶寬之需求就比較低，也就使得Gm-C的架構可以使用比較少的功耗，實現出相同的環路濾波器轉換方程式。

然而，Gm-C的架構因為是開回路架構，所以比起Active-RC的架構，線性度較差，Gm-C架構所貢獻的電路噪聲也較Active-RC大。因此，Gm-C電路通常只能取代環路濾波器中部分的積分器;而在CTDSM中信號擺伏比較大的地方或是CTDSM的輸入端，這些對線性度以及信雜比要求較高，通常還是會采用Active-RC的架構。

Gm-C的架構比起Active-RC架構還有一個缺點，一般Active-RC架構因為是負回授架構，所以會有虛短路(Virtual Short)點可以將輸入信號以及回授信號做相加減;但是，因Gm-C電路比較屬于開回路架構，并沒有明顯的虛短路點可以做信號相加減，因此在環路濾波器架構的選取上，比起用Active-RC的方式實現，就會比較受限。

另一方面，為了提升環路濾波器的階數，同時希望達到低功耗，有些方案會適當的引入電壓控制式振蕩器(VCO)電路，以同時達到一階積分效果以及量化的功能。正因為VCO這項將兩者功能合而為一的特性，因此能夠有效地降低功率消耗。

至于為什么VCO就可以將積分和量化兩項功能合而為一，主要是因為VCO在時域上的操作是依據輸入電壓的不同。VCO電路會振蕩在不同的頻率，而頻率的積分會是相位，因此，只要用一個具有固定相位的信號，和VCO的輸出信號做比較，就可以得到VCO在一個采樣周期內的相位變化量。等效上就是得到對輸入信號積分一個周期后的變化量，這樣不但可以使得輸入電壓因為通過VCO的關系有積分效果，并且輸入電壓因為VCO也會對應到相位信息。

透過和固定相位的參考頻率做比較(通常通過簡單的D Flip-Flop就可以實現以及固定頻率的頻率)，可以得到相位是領先或是落后的信息。而得到量化過后的結果，也就是說藉由VCO電路，可以同時實現積分以及量化運算，亦即把積分器以及量化器合而為一，達到降低功耗的目標。

由以下VCO簡單的公式推導，可以了解到VCO電路在頻域上，的確具有一階積分的效果：

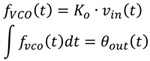
......公式12

Ko:振蕩頻率的增益

fVCO:VCO的振蕩頻率

out:VCO的輸出相位

Vin:VCO的輸入電壓(控制電壓)

此應用的VCO電路通常使用環形振蕩器(Ring Oscillator)(圖8)，因為環形振蕩器可以提供多相位，也就是可以將相位的變化量，區分為更多的狀態，等效出多位(多位)量化器的效果，壓抑量化誤差。然而，因為是采用環形振蕩器，壓控環形振蕩器的線性調變范圍很小，因此如果設計不好，很容易產生額外的Harmonic Tone，這是此一架構的缺點。

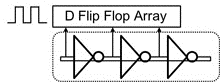
圖8 多級環形振蕩電路

此外，還有另外一種方法，就是引入雙T型濾波器(Twin-T Filter)(圖9)。此種濾波器的特性就是可以只使用一顆運算放大器，配合特別設計過的電阻、電容網絡，即可得到二階的積分效果;換句話說，就是T型濾波器的架構可以只使用一顆運算放大器，就能實現出原先需要兩個Active-RC積分器才能實現的系統方程式。

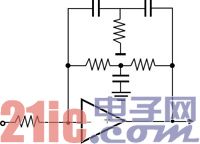
圖9　雙T型濾波器

很明顯的，這個方法可以有效降低運算放大器的使用數量，等效上就是降低環路濾波器的硬件以及功耗。但是這樣的方法通常因為只用到一顆運算放大器，就可以實現兩階積分的方程式，比起原先使用兩個獨立積分器來實現同樣的系統方程式，虛短路的點比較少，而使得在系統參數的設系上，會比較受限。設計自由度會比使用兩顆單獨的運算放大器還低。

綜合上述各種架構做一個簡單的結論，一般最常見實現環路濾波器的方式是Active-RC架構，但是為了更進一步降低功耗，所以有許多方案會采用Gm-C、VCO-Based、Twin-T等方式實現環路濾波器。圖10對環路濾波器的實現方式做了一些簡單的結論。

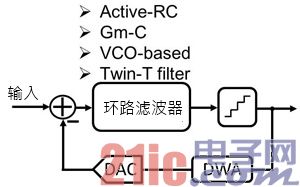
圖10　環路濾波器的各種實現方法

DWA處理消除DAC非線性

誤差

回授路徑上的DAC，如果是使用多位DAC，則DAC的非線性會限制了CTDSM的信號噪聲失真比(Signal to Noise and Distortion Ratio, SNDR)。DAC的非線性誤差可以被視為一個除了電路噪聲以外，額外添加的噪聲源，此噪聲正是因為DAC中各個子電路(Unit Cell)之間的不匹配。要解決這個問題，最直接的方法就是采用單位元的DAC架構(1Bit DAC)，因為只有一個位，就沒有所謂不匹配的問題。

但是采用單位元DAC又會衍生其他問題，例如單位元DAC系統中的積分器相較于多位會比較難設計;同時，單位元DAC也對時序信號抖動(Clock Jitter)此一非理想效應更敏感。如果想要使用多位DAC，但是又想要消除非線性度對CTDSM的影響，最常被使用的方式，就是將DAC的輸入數字碼做適當的處理，也就是所謂DWA的處理。

處理的算法基本方向，就是讓不同的DAC Cells平均地被使用。正因為每個DAC Cells都被平均的使用，所以DAC Cells之間的不匹配效應就會受到一定程度的壓抑，而使得整體CTDSM可以有更高規格的表現。

一般來說，做這樣的信號處理，必須要等到量化器的輸出都已經穩定，才可以做進一步的運算。量化器輸出經過處理后才會被送到DAC的輸入，因而此一電路在回授路徑上，也會貢獻額外的時間延遲，使系統容易振蕩，所以在估計整個CTDSM的系統穩定度時，須要將此一電路所貢獻的延遲適當地考慮進去。

在DAC電路上，最適合用于高速的架構莫過于電流導引(Current Steering)。DAC設計上，最大的問題除了線性度以外(通常會配合DWA電路加以解決)，另外就是電路熱噪聲的問題。目前面對電路噪聲問題，最好的解決方法就是拉高DAC電源電壓，使熱噪聲可以降低，此外鮮少有比較好的解決方法。

本篇文章分為主要兩個部分，在第一部分，介紹了DSM基本的架構以及操作原理，包含過采樣(Oversampling)、噪聲整形(Noise Shaping)等概念;第二部分則是更進一步介紹了CTDSM各部分子區塊的電路架構，包含環路濾波器、量化器、DWA電路以及ADC。針對各個部分，本文亦介紹了許多現今常被使用的技術以及其優缺點。