摘要：針對一種復雜的、較難建立精確模型的空間桁架，研究了其建模、主動桿位置優化及振動控制的問題。文中首先建立了空間桁架的機理模型。然后設計了壓電主動桿，選取一種不依賴于控制律的基于能量的優化準則，并基于所建立的模型對其在空間桁架中的安裝位置進行了優化。最后對于空間桁架這種并聯結構，設計了一種不依賴于被控對象精確模型的自抗擾控制器。仿真算例表明本文所設計方法的有效性。

1 引言

隨著對太空探索的不斷深入以及我國空間光學技術的迅速發展，人們對于太空中航天器的工作精度和穩定運行等方面的研究也越來越深入，特別是航天器中的撓性桁架結構。當有外界擾動作用在桁架上時，由于桁架結構自身所具有的結構特性和太空中低阻尼環境等因素的原因，桁架結構易產生非期望的振動，從而影響航天器的正常工作。因此對于航天器內桁架結構的振動控制方面進行研究具有重大現實意義。

目前，在桁架結構的控制問題中，大多是將主動構件內嵌于桁架結構中，從而構成智能結構，并以主動構件為核心原件，對智能結構進行控制。在主動構件的選擇中，由于壓電材料所具有的質量輕、響應快、低功耗等特點，因此被廣泛應用于空間桁架的振動控制之中。本文以壓電材料為基礎，設計了壓電主動桿。針對壓電主動構件的位置優化問題，目前已有基于能控/能觀性的優化準則、基于系統能量的優化準則等、考慮到太空中能量較為珍貴，本文選擇了一種以最小驅動電壓產生最大驅動力的優化準則。

目前對于桁架結構的主動振動控制已有多種方法，如正位置反饋控制、模態控制法、最優控制、模糊控制等方法。但由于桁架結構具有較大的復雜性，獲得其精確的數學模型是較為困難的。因此本文選擇了一種不依賴于被控對象精確模型的自抗擾控制器，通過對本文中所建立的桁架模型進行仿真實驗，驗證了自抗擾控制器的有效性。

2 空間桁架結構建模

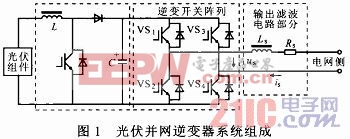
所需控制的空間桁架節點編號如圖1所示：

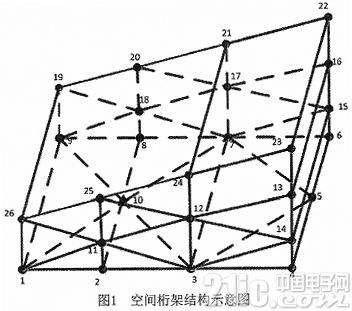
所設計的結構主要由梁單元組成，共有63根柔性梁，26個節點，其中底面的2、3、7、8節點為固定在地面的約束節點，激振力施加于底面的10號節點豎直方向。基于有限元的方法，可以獲得該結構的動力學方程為：

通過求解式(3)所得出的，代回模態變換從而得出各節點位移。

3 壓電主動桿設計及位置優化

由于壓電材料具有正、逆壓電效應，是以其既可作為作動器，也可作為傳感器，并且具有質量輕、響應快、低功耗和易裝配等特點，因此其廣泛的應用于桁架結構的振動控制中。

3.1 壓電主動桿的設計

由于壓電片的壓電應變系數d33一般很小，因此單個壓電片所能輸出的位移非常小。而對于在實際工程應用中的主動控制構件來說，即需要具有能夠滿足需求的輸出位移量，同時也要求其能承擔住一定的壓力。而如果只通過一片壓電片，在輸入電壓受到限制的情況下，一般無法達到實際的需求。因此通過設計多個壓電片以力學上串聯、電學上并聯的方法堆疊在一起構成壓電堆，則可以克服較低電壓驅動下單個壓電片位移過小的缺點，通過多個壓電片變形量的線性疊加，則可以使用較低的電壓，獲得較大的輸出位移，從而增加了輸出的位移量，滿足了實際的需求。

壓電堆的輸出位移為：

其中，δi為單個壓電片的輸出位移，n為壓電片的個數，l為厚度，是恒定電場下的彈性柔順系數，d33為壓電應變系數，Ks稱為壓電堆的等效剛度，ds稱為壓電堆等效壓電應變常數，F為軸向所受的力，V為軸向所施加的電壓，A為截面積。

采用180片壓電片疊加構成壓電堆，然后基于壓電堆，設計了壓電主動桿，其結構圖如圖2所示。

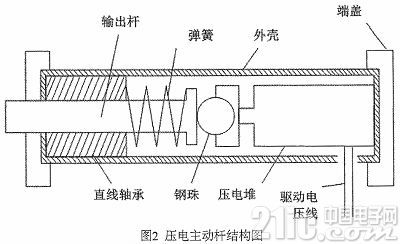
壓電主動桿的輸出位移和輸出力是進行壓電主動桿設計時所需考慮的重點內容。本文所設計的壓電主動桿主要由壓電堆、直線軸承、鋼珠和外部包裝的鋼殼等幾部件構成。

壓電堆內部放置了碟片彈簧進行預壓，使壓電堆始終工作在受壓狀態并保證其內部壓電片之間緊密相連。但是為了保證壓主動桿內部各部件之間不存在間隙，還需要在主動桿內部設計一個彈簧，以保證主動桿內部各零件之間緊密接觸。同時，在壓電堆的一側使用鋼珠作為傳力裝置以保證壓電堆只會受到外部軸向載荷的作用，從而避免其可能出現承受彎曲載荷的情況。同時，為了減小輸出桿在運動時所產生的摩擦，使用直線軸承內套輸出桿，以保證輸出桿靠近鋼珠端不會與主動桿外殼接觸，并且在直線軸承內要保證足夠的光滑，以最大限度的減小軸向摩擦力。

3.2 主動桿的優化準則

由于在太空中，能源是比較珍貴的資源。所以對于剛架的控制希望是主動桿的振動控制能盡可能的節省電能。因此，總是希望主動桿的安裝位置能夠保證其在使用盡可能小的驅動電壓的情況下輸出最大的控制力。

在式(2)中，令：

A=φTBKv (5)

由上式可以看出，矩陣4是由模態矩陣φT、主動桿的安裝位置矩陣B和主動桿的性能矩陣Kv所組成。因此，矩陣A不僅與系統自身的模態相關，而且很大程度上會受到主動桿的安裝位置和其致動特性的影響，所以稱A為主動桿位置配置矩陣。令：

由上式可以看出，若λ的值越大，則表明模態控制力和控制電壓的比值也就越大，即表示使用的控制電壓較小時，可以產生的模態控制力較大，此時系統的作動效率較高。所以當保證ATA的所有特征值都很大并且分布較為集中時，可以獲得較大的作動效率。如此則可以得出作動器的優化準則為：

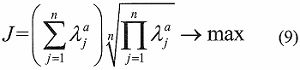
在上述的優化準則中，前半部分是ATA所有特征值的算術平均值，后半部分是所有特征值的幾何平均值，求這兩項乘積的最大值就能得出一個特征值較大且分布集中的A。

3.3 遺傳算法優化結果

使用遺傳算法對前面所得優化準則進行主動桿的位置優化，選取腓為遺傳算法的適應度函數。選擇使用三個主動桿。優化流程圖如圖3所示。

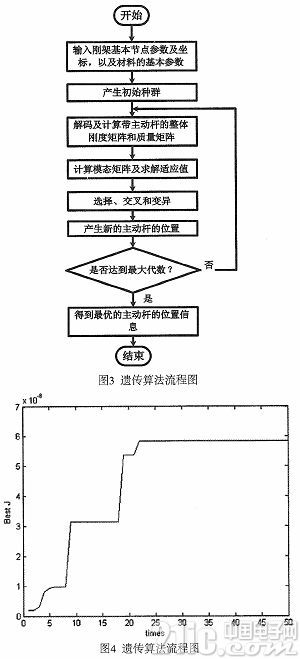
根據流程所示的過程，得出了在剛架中配置3個主動桿時的最優安裝位置如表1所示。圖4為遺傳算法優化過程中最優適應值的迭代過程圖。

4 自抗擾控制器

由于空間桁架結構模型較為復雜，很難獲得其精確的數學模型。而自抗擾控制器不依賴于被控對象的精確模型，并且對于擾動能夠進行很好的抑制，具有較強的魯棒性，因此非常適用于對空間桁架結構的控制之中。

圖5為自抗擾控制器的結構框圖，其主要由擴張狀態觀測器(ESO)和非線性誤差反饋控制率(NLSEF)組成。

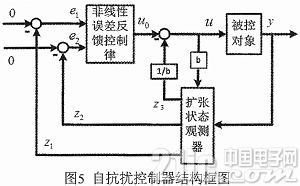
4.1 擴張狀態觀測器

擴張狀態觀測器的核心思想是將系統的外部擾動和內部建模不確定性等未知擾動一起視作“總擾動”，將此“總擾動”擴張成為一個新的狀態變量，從而構建一個能夠觀測此擾動變量的擴張狀態觀測器。

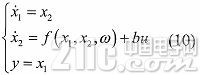
對于二階的非線性系統

式中f(x1，x2，ω)為系統外繞和內部未知因素的總合。將原二階系統中的f(x1，x2，ω)擴張成一個新的狀態變量x3，并記 ，即可得到系統新的狀態方程：

式中，β01、β02和β03等均為觀測器的參數，通過調節這三個參數，可以使得z1(t)→x1(t)、z2(t)→x2(t)和z3(t)→x3(t)。fal函數是為了避免在數值仿真時出現的高頻顫振而設計的冪次函數，此函數在原點周圍具有線性的特性，定義如下：

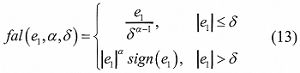
其中δ為線性區間的長度。

4.2 非線性誤差反饋律

為了消除振動，系統輸入的參考位移和速度均為0。根據擴張狀態觀測器輸出的狀態變量的估計值可以得到系統的位移誤差e1和速度誤差e2。從而設計的非線性誤差為：

u0=β1fal(e1，a1，δ)+β2fal(e2，a2，δ) (14)

4. 3 擾動補償

將ESO估計的總擾動z3(t)在控制律中予以補償可得：

將式(15)的控制量輸入到式(10)的二階非線性系統后，可以得到補償后的系統為：

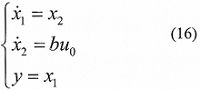
在補償后的控制系統中，已經沒有未知的擾動項，并且將控制系統轉化為了簡單的積分器串聯型的形式。

4.4 并聯系統自抗擾控制

將前面所建立的解耦后的剛架動力學方程分解為下式，這種結構稱為并聯系統結構。

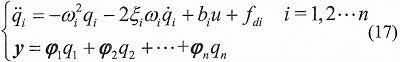
對于不能夠精確確定的剛架結構各階固有頻率、阻尼比或其他一些不確定因素，可將這些不確定的部分認為是內部未知因素，從而可以將以上系統變換為：

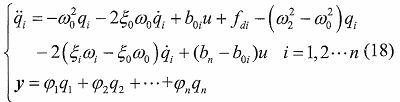
式中的ω0和ξ0均為自己設計的已知參數。

對式(18)進行變換，可得以y作為狀態變量的新系統模型為：

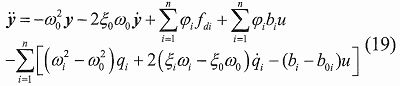
上式中前四項的參數均為已知的，是系統的已知部分、外界已知的激振力和系統的控制律，最后一項是系統未知的部分。

5 自抗擾控制的仿真曲線

使用壓電主動桿對空間桁架進行振動控制，共使用了三個壓電主動桿，1號主動桿安裝位置為底面的節點3—10，2號主動桿為側面的節點15—16以及3號主動桿為頂部節點21—24。安裝好壓電主動桿以后的空間桁架結構前10階固有頻率如表2所示。

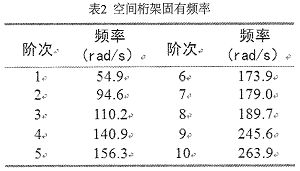
選取底面10號節點的方向為激振點，選取的正弦激振力幅值為10，激振頻率與桁架結構的一階固有頻率相同，為54.9rad/s，這樣可以激起桁架結構模型的一階振動模態，從而激起較大的振動位移。并聯系統中的參數ω0=60，ξ0=0。

控制節點為三個主動桿安裝位置所在的節點，分別為10號節點的x方向，16號節點的z方向和21號節點的y方向，另外選取19號節點的y方向作為觀測節點。

從圖6中可以看出，施加控制以后，在添加了主動桿的三個連接節點可以獲得很好的減振效果，系統在受到外力時激起的振動得到了有效的抑制，并且有效的抑制了19號節點在產生振動時的位移響應。四個節點的振動位移均減少了近兩個數量級。

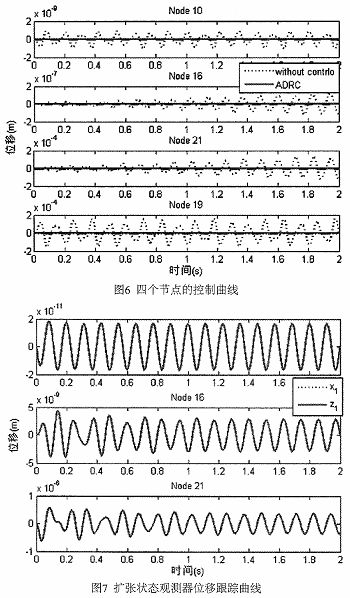
圖7和圖8分別為擴張狀態觀測器輸出的跟蹤位移和速度益線，從圖中可以看出，擴張狀態觀測器觀測獲得的三個控制節點的位移和速度曲線基本與原系統的速度和位移曲線一致，說明了擴張狀態觀測器很好的跟蹤了原系統的狀態。

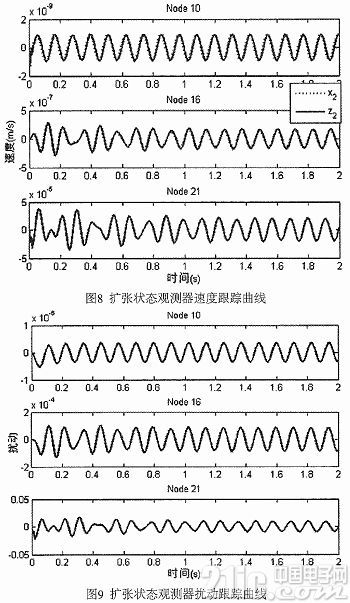
圖9為擴張狀態觀測器觀測得到的三個控制器的擾動跟蹤曲線。由于在實際控制中，擾動是不可被精確得知的，但由于擴張狀態觀測器對系統輸出的位移和速度的跟蹤效果很好，所以可以認為所設計的擴張狀態觀測器也能夠準確的跟蹤上總擾動。

所施加的正弦擾動幅值為30，頻率分別為50rad/s、200rad/s、600rad/s，在不同擾動頻率下觀測獲得的四個節點控制曲線如圖10和圖11所示。

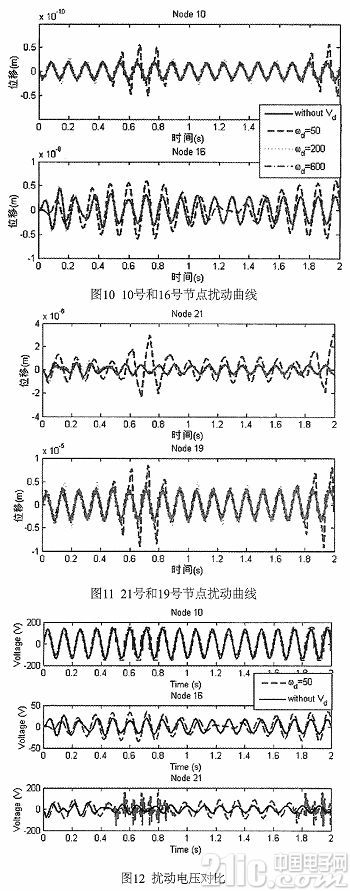
從圖10和圖11中可以看出，在控制輸入端增加了三種不同頻率的擾動以后，控制器的控制效果依然很好。其中當輸入頻率為200rad/s和 600rad/s時，控制器的輸出基本和不添加擾動時的一樣，僅在當擾動頻率為50rad/s時，控制效果會相對于沒有擾動時的控制效果略有變差，但仍然具有很好的振動抑制作用。施加擾動頻率為50rad/s時控制效果略有變差的原因是因為此時擾動信號的頻率與激振力的頻率相近，所以會對系統有一定的影響。因此，可以看出自抗擾控制器具有較好的魯棒性。

圖12中對比了未加擾動時和施加了頻率為50rad/s擾動時三個主動桿的控制電壓的差別。由于主動桿最大所能承受的電壓為1 50V，如果主動桿輸入的電壓超過150V，則有可能對其造成很大的損害，所以對于主動桿的輸入電壓需要進行限幅。從上圖中可以看出，控制21號節點的主動桿在0.5s到0.8s和1.75s到2s左右時，已經達到了最大的輸入電壓，所以位移響應的控制效果也會有所下降。而這也與圖9和圖1 0中所示的位移響應在0.5s到0.8s和1.75s到2s左右時的位移控制效果相對最差所相對應。在這2個時間段內，擾動會對系統造成較大的影響，但在這段時間過后，系統依然可以獲得較好的振動控制效果。

6 結論

本文對于所建立的空間桁架模型，選取了壓電主動桿作為其控制元件，建立了桁架結構的動力學方程。然后設計了壓電主動桿，并使用基于能量的優化準則和遺傳算法進行了主動桿的位置優化。在此基礎上，運用了由擴張狀態觀測器和非線性誤差反饋控制律組成的自抗擾控制器對建立的模型進行了仿真分析。通過擴張狀態觀測器對系統狀態的準確觀測，從而實現系統中未知擾動的補償。仿真結果表明，本文所設計的自抗擾控制器能夠有效、準確的對空間桁架結構的振動進行控制。最后在控制系統中加入正弦擾動，驗證了自抗擾控制器有較好的魯棒性。