摘要：基于內容的音樂分析是計算機音樂智能處理領域的重要分支，其中音符的分割和識別是關鍵技術之一。本文首先根據音級輪廓特征(PCP)，對音樂進行特征提取，將幀集通過行列式點過程(DPP)進行建模，最后根據最大后驗概率估計(MAP)選出幀子集，從而實現音符的分割。DPP將復雜的概率計算轉換為簡單的行列式計算，減少了計算量。在鋼琴音樂片段多音符的的識別中，得到了67.3%的正確率，解決了多音符的切分識別難題。

1 引言

　　對音符進行識別是音樂信號分析處理領域中重要的研究內容。音符識別技術在音樂數據庫的建立、管理和索引中具有重要的應用價值，如何準確地進行音符分割是檢索系統中較困難的問題^[1]。音符識別技術可以便捷地實現樂譜的計算機錄入，在音樂內容檢索、計算機輔助鋼琴教學、音樂作品數字化等領域具有廣闊的應用前景。隨著計算機多媒體技術、數字信號處理技術等不斷發展，越來越多的音樂作品進入數字化的軌道，基于計算機的音樂識別、樂譜跟蹤、音樂分類等一系列課題也被越來越多的學者關注。現有音符分割的方法大多是依據能量分割。文獻[2]提出了使用聲音的頻譜參數，利用計算音符的自相似性進行音符分割。文獻[3]憑借能量特征確定哼唱的起點和終點，通過設定動態門限的方法實現音符分割。近些年，國內學者的研究主要集中在和弦的識別以及單音符的識別上，對于多音符的識別較為欠缺。本文將運用DPP識別模型，對多音符進行分割識別。

　　行列式點過程模型(DPP)在圖片分割、文本摘要和商品推薦系統中都有成功的應用。DPP將復雜的概率計算轉換成簡單的行列式的計算，減少了計算量，提高了運行速度，并且很好地解決了負相關的問題^[4]。本文首先將音樂信號進行PCP特征提取，在識別階段運用DPP進行建模，并用300段標記好的訓練集對模型參數進行訓練，從而完成音符的自動分割識別。

2 DPP音符切分

2.1 PCP特征提取

　　音級輪廓特征(PCP)是音樂信息檢索中廣泛使用的一種信號特征。PCP將頻譜重建為音級譜，將音樂信號能量映射到12個音級上。

　　PCP特征計算：

　　第1步：分幀處理，將時域離散信號分為重疊的幀。

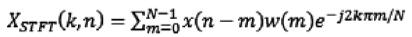(1)

　　k表示頻率坐標，n表示短時傅里葉變換窗口的中心，w(m)為漢明窗。

　　第2步：頻譜映射,強X_STFT(k,n)映射為一個十二維的向量p(k)，每維表征了一個半音級的強度。映射公式為：

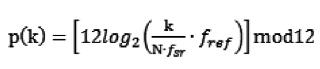　(2)

　　其中，f_ref為參考頻率，f_sr為采樣率。

　　第3步：將各個音級相對應的頻率點的頻率值進行累加，得到每個時間片段的各個PCP分量的值，公式如下：

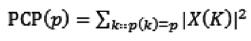(3)

　　其中p=0，1，…，11。PCP通過一個12維的向量來表示一個音級，它反映了音符在每一個12半音音程中半音階刻度下的相對強度^[5]。

2.2 行列式點過程模型

2.2.1 DPP概述

　　行列式點過程(DPP)是一種概率模型，它通過核矩陣的行列式來給出每一個子集的概率^[6]。離散集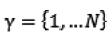上的點過程P是一個2^γ上的一個概率測度，當Y是P的一個隨機子集時，P就被稱作行列式點過程：

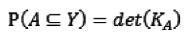(4)

　　其中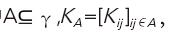K為邊緣概率核矩陣，K包含了計算A的概率的所有信息。K_ij的值越大代表i和j越不可能同時發生，因此DPP適用于對突出差異性的集合進行建模。從圖1可以看到，相比于獨立抽樣，DPP抽樣的點集覆蓋的信息更廣，全局性更好[7]。

2.2.2 模型的建立

　　K矩陣定義了一種邊緣概率，為了方便對真實數據進行建模，通常采用L矩陣集來代替K，L定義了每一種子集概率，為最優化提供了一個方便的表述。一個通過正定矩陣L定義的DPP如下：

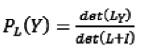　(5)

　　其中，I為N乘N單位矩陣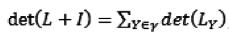，為歸一化因子，K=(L+I)^-1L。

　　對L進行格萊姆分解^[8]：

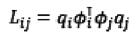(6)

　　qi∈R+表示i幀的Q值，即為能量;φ_i∈Rⁿ，||φ_i||₂=1為i幀的標準特征向量，由i幀的PCP特征向量做歸一化得到。所以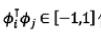代表了i幀和j幀的相似度。

　　圖2為DPP的幾何描述，每一幀都由一個向量表示。圖a向量所圍成的面積即為幀i和幀j的聯合概率;圖b增加了幀j的Q值，聯合概率也增加了;圖c提高了幀i和幀j的相似度，聯合概率相應地減小。

2.2.3 建立目標函數

　　通過在條件行列式點過程模型中加入參數，來實現有監督的學習模型。對于訓練集，輸入集合X為音樂每一個音符的一幀組成的點集，y(X)為該音樂內所有備選的點集。所以在參數θ下，給定的輸入集X，輸出集Y的條件概率如下:

(7)

　　其中。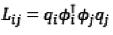

　　只要保證相似度特征矩陣是正定的，相似度特征向量φ_i(X)可任由期望的測量值構成，也可以是無限維度的。我們用對數線性模型計算Q值：

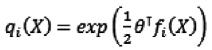(8)

　　其中f_i(X)∈R^m為幀i表征Q值的特征向量，θ∈R^m為參數向量。

　　利用最大似然估計(MLE)建立目標函數：

(9)

　　最優化L是基于一致性假設的。如果訓練數據準確地參數θ* 滿足條件行列式點過程分布，那么當時，學習到的參數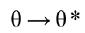。當然現實中的數據不可能準確地遵循任何確切的模型，但是最大似然近似依然能夠較好地矯正DPP產生合理的概率估計，因為使L最大相當于令訓練數據的對數損耗最小。

　　本文利用下降梯度算法，來最優化對數似然，L(θ)梯度如下：

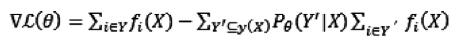(10)

2.2.4 最大后驗概率估計(MAP)

　　我們需要用學習到的參數θ來預測測試集X，得到最終的點集Y。一種方法是從DPP條件分布中抽樣，這將需要立方的時間復雜度[9]，本文將采用最大后驗估計(MAP)來進行預測。在約束條件下的Y^MAP定義如下：

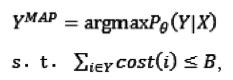(11)

　　其中cost(i)為幀i的能量，B為總能量的門限值，計算Y^MAP是NP困難問題^[10]，我們這里做兩個近似。第一，我們通過抽樣獲得大量的子集Y，然后通過約束條件選擇可能性最大的一個;第二，注意到公式(11)為一個子模塊，我們可以用一個簡單的貪婪算法來近似它。對于單調子模塊問題，這種算法有合理的近似保證^[11-12]。

3 實驗與結果分析

3.1 實驗環境與數據

　　本文的實驗環境為安裝有Matlab2010A 的PC 機，在356首符合條件的鋼琴曲片段中，隨機選出300個音樂片段作為訓練樣本數據，其余的56個片段作為測試數據。訓練、測試音樂片段的平均時間長度為6.8s，平均多音音符15個。從訓練模型庫中可以看出經過300個音樂片段訓練后得到的多音音符基本覆蓋了鋼琴88個單音所構成的多音符組合。表1是幾種多音符系統的識別率(多音符中單音符數超過3)。

3.2 結果分析

　　本課題所研究的基于DPP的多音符識別系統其識別率提高了近5%。與時頻域、統計法等識別相比，基于DPP的模式識別法雖然需要對樣本進行先期訓練，但是由于DPP對多音符特征轉換較為精確的建模，為多音符的正確識別奠定了基礎。在模型建立過程中，對于相近多音符的建模是本課題識別率較低的原因之一。比如，對于多音符A1C2F2 和A1C3F3，在特征提取過程中，二者相差的只是C2和C3兩音符上的頻率帶能量差，而根據鋼琴十二平均律的物理特性，二者成倍頻關系，這就為PCP特征提取帶來極大的困難。

4 結束語

　　本文介紹了利用DPP模型對鋼琴曲進行多音符自動分割識別的初步研究結果。在運用PCP特征的的基礎上，音符識別率達到了67.2%。但是，根據實驗中出現的問題，本系統還存在諸多需進一步研究改進的地方。首先，在對多音符的建模時，由于相近多音符的特征差異小，導致模型近似，出現誤識別，這就需要采用新的多音符特征;其次，DPP模型趨向于選擇差異性大的子集，所以對于短時有內大量重復旋律的音樂，DPP的分割正確率并不理想。但是，DPP將復雜的概率計算轉換成簡單的行列式計算，在計算速度上大大優于MRF^[13]，在對海量音樂進行分割識別時，DPP的優勢將更加明顯。

參考文獻：

　　[1]Meek C.J,Birminghan W.P Can't Sing:A Comprehensive Error Model for Sung Music Queries[C]//Proc.ofISMIR’02.Paris,France:[s.n],2002

　　[2]曹建紅.基于哼唱的音樂檢索技術研究[D].南京:南京理工大學,2009

　　[3]Foote,J.,Automatic Autio Segmentation using a Measure of Audio Novelty.In Proceeding of IEEE Intermational Conference on Multimedia and Expo,vol.i,pp.452-455,July 30,2000

　　[4]A. Kulesza and B. Taskar, Determinantal Point Processes for Machine Learning, Foundations and Trends in Machine Learning: Vol. 5, No 2-3, 2012

　　[5]王峰. 美爾音級輪廓特征在音樂和弦識別算法中的應用研究[D]. 太原: 太原理工大學, 2010

　　[6]Johansson. Determinantal processes with number variance saturation. Communications in

　　mathematical physics, 252(1):111–148, 2004

　　[7]Hough, M. Krishnapur, Y. Peres, and B. Vir_ag. Determinantal processes and independence. Probability Surveys, 3:206-229, 2006

　　[8]Kulesza and B. Taskar. Structured determinantal point processes. In Proc. NIPS, 2010

　　[9]A. Kulesza and B. Taskar. Learning Determinantal Point Processes. In Proc. UAI, 2011

　　[10]Ko, J. Lee, and M. Queyranne. An exact algorithm for maximum entropy sampling. Operations

　　Research, 43(4):684{691, 1995. ISSN 0030-364X

　　[11]Hui Lin and Jeff Bilmes. Multi-document summarization via budgeted maximization of submodular functions. In Proc. NAACL/HLT, 2010

　　[12]Krause and C. Guestrin. A note on the budgeted maximization of submodular functions.Technical Rep. No. CMU-CALD, 5:103, 2005

　　[13]Borodin. Determinantal Point Processes. arXiv:0911.1153, 2009

本文來源于中國科技期刊《電子產品世界》2016年第4期第28頁，歡迎您寫論文時引用，并注明出處。