1　引言

隨著社會的發展和醫療技術的進步，人們對身體健康的關心程度越來越高。醫學影像已經不再是僅供醫生參考的信息而成為診斷疾病的重要依據。在網絡傳輸條件下的圖像壓縮編碼成為建立數字化醫院的關鍵技術。

目前，二維圖像的壓縮標準有JPEG、GIF及采用了小波變換的JPEG2000等。醫學圖像具有特殊性，它一般不允許丟失有用的細節信息。傳統的DCT（Discrete Cosine Transform，離散余弦變換）和第一代小波在圖像變換后會產生浮點數，因而必須對變換后的數據進行量化處理，這樣就會產生不同程度的失真。可見，量化器的設計是決定圖像保真度的關鍵環節。由于第二代小波采用提升方法能夠實現整數變換，因而能夠實現圖像的無損壓縮，顯然，它是一種很適于醫學圖像的壓縮方法。

2　SPIHT算法

基于分層樹的集合劃分算法（Set Partitioning inHierarchical Trees，SPIHT）改進了內嵌零樹編碼算法（EZW）。在對圖像進行小波變換后，它更有效地利用了不同尺度子帶重要系數間的相似性。它呈現出良好的特性：不依賴傅立葉變換而在空間域中構造小波；較高的PSNR（Peak Signal Noise Ratio，峰值信噪比）保證了良好的重現圖像質量；整數運算利于實現實時快速編解碼和網絡傳輸；圖像碼流的逐漸呈現便于用戶上網檢索感興趣的圖像。

SPIHT算法對圖像信息采用如下的編碼步驟。

首先，定義三個隊列：不顯著性系數隊列LIP，顯著性系數隊列LSP和不顯著性集合隊列LIS。

設，O（i，j）表示節點（i，j）的直接節點的集合；D（i，j）表示節點（i，j）的子節點集合；L（i，j）表示子節點中排除直接節點后的集合。

在隊列中，每個元素由一個坐標唯一識別，它在LIP和LSP中代表孤立系數（無子節點的根節點），在LIS中代表第一類元素的D（i，j）或者第二類元素的L（i，j）。

對某個閾值T進行顯著性測試。將大于T的元素移入LSP，并在LIP隊列中移除該元素。對LIS也進行同樣的測試，將顯著的元素移入LSP，其他的再進行樹的分裂。

用類C＋＋語言描述的SPIHT算法如下：

第一步，閾值T和三個隊列（LSP、LIS和LIP）初始化。

的坐標；

（2）if（x，y）是第二類元素，對L（i，j）進行顯著性測試

if（L（i，j））＝＝1 all（k，l）∈O（i，j）作為第一類元素移入LIS，從LIS出隊。

第三步，比特傳輸／存儲。將LSP中的每個系數轉化成二進制傳輸／存儲。

第四步，閾值更新并轉至第二步：T／＝2；gotostep2。

3　提升方案與第二代小波

提升方法構造小波分為分裂、預測和更新三個步驟。

3．1　分裂（split）

將一原始信號序列Sj按偶數和奇數序號分成兩個較小的、互不相交的小波子集Sj－1和dj－1：

3．2　預測（predict）

由于數據間存在相關性，因而可以定義一個預測算子P，使dj－1＝P（Sj－1），這樣可用相鄰的偶數序列來預測奇數序列。若用dj－1與P（Sj－1）的差值代替dj－1，則其數據量要比原始dj－1小得多。

最簡單的情況下，取兩個相鄰偶數序號所在數據的均值作為它們間奇數序號所在數據的預測值。即，

3．3　更新（update）

由于上述兩個過程一般不能保持原圖像中的某些整體性質（如亮度），為此，我們要構造一個U算子去更新Sj－1，使之保持原有數據集的某些特性。

4 編／解碼方案

本文中前端采用第二代小波（lifting wavelet），接著對小波系數采用SPIHT算法，然后，采用Amir Said的自適應算術編碼。解碼是編碼的逆過程，包括與正向SPIHT對應的三個步驟：恢復更新、恢復預測和合并（merge）。編／解碼方案如圖1所示。

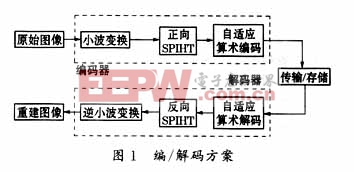
如果前端利用第一代小波進行有損壓縮，可以取得更高的壓縮比。顯然，第二代小波變換對數據壓縮的高保真性與高壓縮比的要求是矛盾的。

5 實驗結果及結論

對上一編碼方案，我們分別對醫學圖像和Lena圖像進行了測試，碼率bbp采用bit／pixel。由于采用了無損壓縮方案，所以，表1中的三種不同編碼方法均有PSNR＝∞。

從表1可以看出，在對標準測試圖像Lena進行編碼時性能差別不是很大，但由于一般的醫學圖像的邊緣存在大量的“零像素”，因此，在用SPIHT編碼時可以產生大量的“零樹”，大大減少了數據量。所以，在對醫學圖像進行壓縮時，更適合采用本文的方法。

進一步的分析表明，與目前廣為使用的JPEG相比較，本壓縮方案占用內存小、編碼效率高且無馬賽克現象。在低碼率時，兩者間的差距更為明顯。如果該方案采用并行快速算法和硬件實現，其實時性會進一步提高，所以，該醫學圖像壓縮方案有較好的應用前景。