摘要：提出了一種基于修正的M距離輻射源識別的新方法。該方法對各特征參數作加權值處理，得到一種新的相似性度量標準，大大提高了識別的準確性。通過計算機仿真，驗證了該方法的合理性與有效性。

現代戰場電磁環境日益密集、復雜，如何快速、準確地對輻射源進行識別已成為電磁斗爭領域的一項緊迫任務。一般來說，無源探測系統通過對輻射源輻射信號的處理，得到反映輻射源特征的特征量，由這些特征量根據一定的算法完成對輻射源的識別。這里提到的識別主要是指對輻射源的類型作出判斷，若能預先知道輻射源與載體之間的搭配關系，則可進一步實現對輻射源載體的識別[1]。目前，對輻射源識別方法的研究很多，包括人工識別方法、傳統的數據處理識別方法、智能化識別方法等[3[4]。人工識別方法是運用人的知識、經驗，進行分析和推理，作出判斷，不能適應復雜的電磁環境。傳統的數據處理識別是利用計算機技術、數字技術進行識別(如數據庫查詢識別、統計模式識別等)。這類識別方法在待識別雷達信號數據不全或新出現信號時，識別結果難盡人意。智能化識別方法一般比較復雜，難以實現。本文從統計學理論出發，提出了一種基于修正的M距離的輻射源識別法，對輻射源識別問題進行了一些有意義的研究。

1 問題描述

對于現有的數據庫或知識庫，輻射源個體識別過程就是將偵察所得信號與輻射源數據庫中的已知信號相比較，根據某一判決規則，使按該規則對被識別對象進行識別所造成的錯誤識別率最小或引起的損失最小，從而確定該信號的類屬。簡單地說就是一個分類問題[2]。其判斷的依據主要是看兩信號的相似性程度，這涉及到相似性度量標準的問題。為了有效地實現分類識別，需對原始偵察數據進行處理，得到最能反映分類本質的特征。一般把原始數據構成的空間叫測量空間，把分類識別賴以進行的空間叫做特征空間。如果用一組特征參數描述輻射源信號，由這組特征參數所構成的向量即為特征空間中的一個點，此時，點間的距離函數可以作為相似性度量的一個標準。這樣，在實際過程中可以依據距離的大小作為模式分類的依據。現在的問題就歸結為選擇什么樣的距離作為相識性度量的標準，從而實現識別、分類。

在輻射源識別中，常采用M距離作為相似性度量的標準。M距離又稱為馬氏距離，這里的M代表英文Maharanobis。在數理統計中，稱常數

r為a到b的M距離。其中a、b為m維列向量。下面以雷達為例，討論輻射源泉識別中M距離的應用。

對于雷達這樣的多特征對象，采用多元正態分布的概率模型，其概率密度函數定義為：

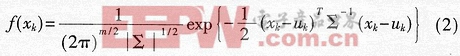
式（2）中，xk=[xk1,xk2,…，xkm]T,xki,i=1,2,…,m是表征第k類雷達信號的一組特征參數，它們對信號的識別起關鍵作用。例如xk1取載頻f,xk2取重頻間隔PRI，xk3取脈寬PW，xk4取天線掃描周期Ta等。這里，uk=[uk1,uk2,…,ukm]T為xk的m維均值向量，∑為xk的mxm維協方差矩陣，即∑=E{（xk-uk）(xk-uk)T}。由M距離的定義知道，對于特征空間的兩點xk和uk來說，M（xk,uk）表示空間上任意一點到某一考慮該特征分布中心的距離，具體表示為：

為特征矢量xk的每一個分量的方差，對于具體的偵察設備來說即為參數容差值。

事實上，M距離相對其他距離如歐氏距離而言具有以下優點：首先，M距離是歐幾里德空間中非均勻分布的歸一化距離，不用考慮各特征參數的量綱；其次，M距離是根據整個空間上的特征分布情況來作為判別依據的，排除了模式樣本之間的相關性影響；同時，給出的結果是一個數值，判斷標準簡單易行，也為更高一級的分析提供了較可靠的依據。但是，M距離的定義中并沒有考慮每一個特征參數在識別過程中所起作用即權重的大小。從式(4)可以看出，各特征參數在識別中是作等權值處理的，不符合實際情況。因此，采用修正的M距離作為相似性度量標準。定義新的距離函數如下：

其中W為權系數矩陣，表示如下：

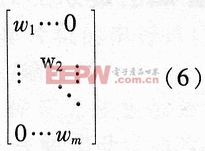
且滿足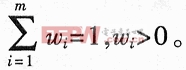則（4）式可表示為：

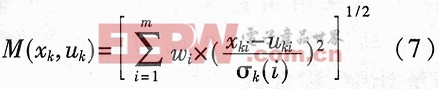
這樣，得到了一個新的相似性度量標準。

2 權系數的設置

一般來說，對輻射源目標特征參數之間重要性沒有任何先驗信息，采用等加權處理方法，如式(4)所示。它是修正的M距離的一個特例。如果是具有一定先驗信息的情況，此時權值可根據先驗信息確定。但在實際工，作中，先驗信息很難得到，此時可以采用如下的熵值分

析法確定權系數。

2．1 熵的定義[2]

熵在信息論中是一個非常重要的概念，它是不確定性的一種度量。設集合X中各事件出現的概率用n維概率矢量p=(p1,p2,…,pn)表示，且滿足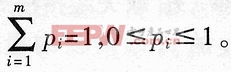則熵定義為：

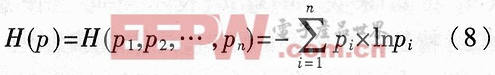
因此，熵H可以看作是n維概率矢量戶p=(p1,p2,…，Pn)的函數，稱為熵函數。

熵函數H(p)具有以下重要性質：

(1)對稱性：概率矢量p=(P1,P2，…，Pn)各分量p1,p2,，…，Pn的次序任意改變時，熵函數H(P)的值不變，即熵值只與集合X總體上的統計特征有關。

(2)非負性：熵函數是一個非負量，即： H(Pl,P2，…，Pn)≥0 (9)

(3)確定性：集合X中只要有一個必然事件，其熵值必為零。

(4)極值性：集合X中各事件以等概率出現時，其熵值為最大，即有：

H(p1,p2,…,pn)≤H（1/n,1/n,…,1/n）=1nn (10)

由熵函數的定義可知，熵值越小，不同類別的分離程度越大。從概率論的角度來看，某一特征的熵值越小則包含的確定性信息越多；反映在分類識別中就是它對識別結果的影響較大，這也意味著設置該特征參數所對應的權值要大一些，以保證識別的精度和準確性。

2.2 熵值分析法設置權重

對于有k類模式的雷達輻射源識別問題，已提取的特片參數共有m個，如式（2）所示。對每一個特征參數Fj;j=1,2,…，m，將其對應的分布區間分為相等的N段，記為rk(j),k=1,2,…,N.注意，這里的分布區間是指k類模式的最大可能的參數分布區間。滿足Fj∈rk(j)的樣本屬于i類的概率為pki(j):

pki(j)=[Nki(j)]/[Nk(j)] (11)

式（11）中，Nk(j)為有Fj∈rk(j)的樣本數，Nki(j)為Nk(j)中屬于第i類的樣本數，于是有：

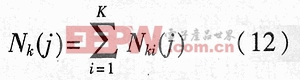
又設pk(j)為一個樣本有Fj∈rk(j)的概率，則有：

pk(j)=[Nk(j)]/N0 (13)

式（12）中N0為總的樣本數，即：

從而定義特片Fj的熵值為：

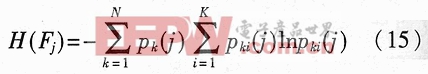
根據熵函數的性質，熵值H(Fi)越小，各類模式在特征Fi上的類間分離性越大，則特征巧對分類的貢獻越大，即在識別過程中的權重越大。如果有Fiεrk(j)的所有樣本都屬于同一類，則有H(Fi)=0。在這種情況下，用這一特征巧就可以實現分類識別。在得到各個特征參數的H(Fi)后，就可以定義相應的歸一化權值如下：

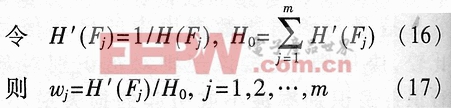
需要注意的是，由于識別過程實際上是將偵察所得信號與輻射源數據庫中的已知信號相比較，因而可以采用輻射源數據庫中的數據作為熵值分析法的樣本。這實際上是充分利用已有的知識數據庫中的分類信息確定各特征參數在識別中的權值，以期得到較好的識別效果。

獲得權系數后，就可根據相似性度量的大小判斷一個特征向量應屬于哪一類。若已知待識別信號為。，顯然滿足M'(s,ui)最小的類ωi與樣本有著最大的相似度。即：

M'(s，9ui)=min(M'(s，uj))→sεωi (18)

其中i，j=1，2，…，K，K為類的總數，ωi表示第i類。

3 仿真實驗及結果分析

在該實驗中以雷達知識數據庫中11類雷達輻射源的識別問題作為研究對象。所采用的描述雷達類型的特征參數為：載頻、重頻間隔、脈寬和天線掃描周期。分段數N=100，經計算得到的各個參數在識別中的權重如表1所示。

表1 各參數在識別中的權重

下面考慮對某個已知類型的雷達的一批偵察數據進行處理，計算對該目標的識別率，得到的識別率與信噪比的關系曲線如圖1所示。

由圖1可以看出，為得到較高的識別率，要求信噪比達到5dB左右。進一步的研究表明該方法對未知的新類型雷達目標具有較好的判斷能力；同時，分段數N的大小及由此決定的分段區間對權值的確定有一定的影響。當N足夠大時，權系數的變化趨向穩定，最終得到的極限值就可以作為確定權系數的依據。

本方法在實際應用中還要注意特征參數的選取和識別權系數的確定，特別是對先驗信息的利用，以期得到更佳的識別效果。