摘要：浮點運算器的核心運算部件是浮點加法器，它是實現浮點指令各種運算的基礎，其設計優化對于提高浮點運算的速度和精度相當關鍵。文章從浮點加法器算法和電路實現的角度給出設計方法，通過VHDL語言在OuartusII中進行設計和驗證，此加法器通過狀態機控制運算，有效地降低了功耗，提高了速度，改善了性能。
關鍵詞：浮點運算；加法器；設計；VHDL；狀態機

在一般的處理器中，浮點加法、減法、轉換和傳送最終都是可以轉換為采用浮點加法器實現，所以浮點加法器的使用頻率高達55％，是使用頻率最高的浮點運算模塊。浮點加法的兩個特點，一是它復雜，二是它被使用的頻率在所有操作里面是最高的，所以它是現代微處理器和數字信號處理器中非常關鍵的部分。因此．浮點加法器的設計對FPU的整體性能十分重要。

1 運算方法
最基本的浮點加法算法需要相對最多的串行運算操作，它需要完成兩個浮點操作數的求和運算，包括尾數部分的求和以及相應修改結果的指數值，而且最終結果必須是符合正IEEE754標準的規格化浮點數。
根據IEEE754浮點數表示方法與運算規則，其表示如公式(1)所示：

公式中：s為尾數的符號；t為指數的符號；e為尾數；f為指數。存儲格式如圖1所示。

為方便浮點數的乘除法運算，文中將e=1．n的表示方法改為e=1n，這樣不斷減少了進行乘除運算后的額外移位操作而且不增加加減法運算的運算量。
一般情況下，在浮點運算中為了提高數據表示的精度，通常需要將一段離散數據在實數軸上集中表示，這就需要對浮點數的表示方法進行限制，因此在浮點數中尾數的位數應大于指數的值，這樣表示的優點是其數據精度相對較高。
本浮點加法模塊，將采用突破浮點數表示方法的上述限制，使指數的值可以遠遠大于尾數的位數，這樣數據的表達范圍增大，實數軸上較寬的一段離散數據就可表達。然而這種做法的缺點是，一方面當數據表示寬度增大后，其精度就會降低，原因是表示的匯聚點距離拉大；另外一種情況是會出現數據移空現象，例如當一個操作數很大，而另一個操作數很小時，如果要進行減法運算，會出現在對階移位的過程中將一個操作數移成了空數據，其值將會變成零。因此當兩個操作數進行加法運算時，假如它們之間的差距很大，就可以不進行運算，直接將較大的操作數直接輸出作為運算結果，就可將無謂操作避免，從而節省運行時間。
對于浮點數加法運算來說，它要求參與運算的兩個操作數有一個共同的特點，那就是指數相同。只有當兩個操作數的指數相同時才能夠進行加法運算。浮點數加法如公式(2)所示：

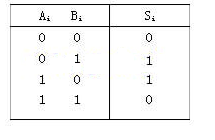
簽于浮點加法運算的特殊要求，兩個浮點操作數存進行運算時需要通過以下幾個步驟完成。第1步進行0操作數的檢查，如果判定兩個操作數中任意一個操作數為零，則沒有必要進行后續一系列的操作，直接輸出結果，從而節省運算時間；第2步，看它們的階碼是否相同，也就是小數點是否對齊，若相同則表示對齊，否則就必須通過對階使小數點對齊，即階碼相同。第3步，對階結束后，進行尾數求和，方法和定點加法運算相同。第4步，對結果進行規格化。第5步，進行必要的舍入處理。另外在進行加法器設計時，將和減法一起進行考慮，采用補碼運算，這樣將來的操作就可以直接調用加法核去完成。