0 引 言
數字信號處理主要研究采用數字序列或符號序列表示信號，并用數字計算方法對這些序列進行處理，以便把信號變換成符合某種需要的形式。在現代數字信號處理中，最常用的變換方法就是離散傅里葉變換(DFT)，然而，它的計算量較大。運算時間長，在某種程度上限制了它的使用范圍。快速傅里葉變換(FFT)的提出使DFT的實現變得接近實時，DFT的應用領域也得以迅速拓展。它在圖像處理、語音分析、雷達、聲納、地震、通信系統、遙感遙測、地質勘探、航空航天、生物醫學等眾多領域都獲得極其廣泛的應用。隨著FPGA技術的高速發展以及EDA技術的成熟，采用FPGA芯片實現FFT已經顯示出巨大的潛力。
目前用FPGA實現的FFT處理器結構大致分為四種：遞歸結構、級聯結構、并行結構和陣列結構。遞歸結構只利用一個碟形運算單元對數據進行規律的循環計算，使用硬件資源較少，但運算時間較長。級聯結構每一級均采用一個獨立的碟形運算單元來處理，相對遞歸結構速度上有所提高，不足之處是增加了延時用的緩沖存儲器使用量。并行結構對一級中的蝶形單元并行實現，陣列結構是將每一級的蝶形運算單元全部并行實現，這兩種結構有很高的運算速度，但消耗的資源過大，一般不采用。為了提高運算速度，特別是為了適應多批數據處理，一般采用級聯結構實現FFT處理器。

1 FFT整體結構設計
在FFT算法中，目前大多使用基-2和基-4算法實現級聯結構的FFT處理器，除此之外，也可采用基-8和基-16算法來實現。隨著基數的增大，對于相同點數的離散數列，處理器所分的級數越少，對緩沖存儲器的需求也越小，因此考慮采用基-16算法來實現FFT處理器，但基-16算法只能實現離散數列點數是16的p次冪的FFT。從而，引入混合基思想來改進基-16算法。
設x(n)為N點有限長序列，其DFT為：

式中：n1=0，1，2，…，r1-1；n2=0，1，2，…，r2-1。將頻率變量k(kN)表示為：
k=k1r1+k0
式中：k1=0，1，…r2-1；k0=0，1，…r1-1。
式(1)可變換為：

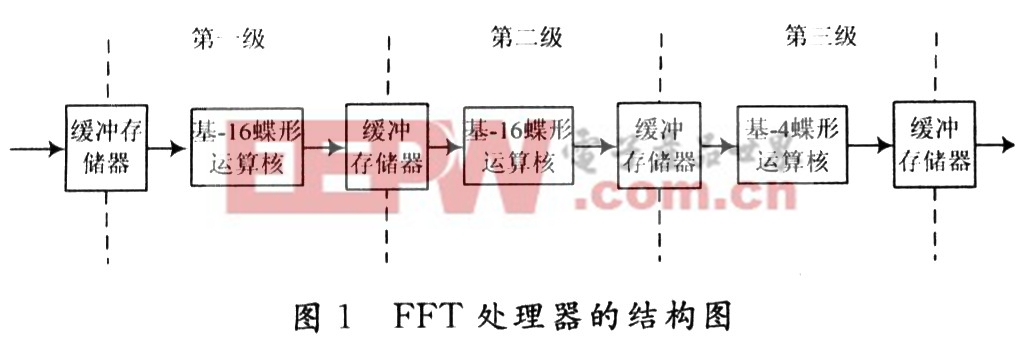
設r1=16P，r2=N／16P=2，4，8，式(2)先將原非16的p次冪的N點FFT分解為16P點的FFT；再分解為N／16P點的FFT。首先對輸入信號進行16P點的FFT運算，然后將結果乘以一個旋轉因子最后將計算出的數據進行一次N／16P點FFT運算，得到的結果即為所需要的N點FFT運算結果。這樣處理，既能減少分解的級數，又能使計算離散數列點數只需是2的整數次冪即可。以1 024點為例，只需分解成兩級基-16運算模塊和一級基-4運算模塊即可實現，其FFT處理器結構圖如圖1所示。在此結構圖的前端增加／減少基-16運算模塊或將最后一級基-4運算模塊改為基-2或基-8運算模塊，就可以實現其他離散數列的點數只需是2的整數次冪的FFT運算。