基于Ansoft仿真分析的SSN解決方案探討
在設計中,最快信號跳變時間為0.17 ns,所以整體設計的截止頻率為3 GHz。為了達到此帶寬,通常需要在MHz信號區域放置很多高頻瓷片電容(nF),在kHz信號區域放置體積較大的電解電容(?滋F)。通過系統設計書可知U17芯片的上升時間約為1 ns,所以它的工作截止頻率約為500 MHz。因此要求在500 MHz頻率范圍內,U17芯片附近電源/地阻抗低于0.825 Ω。
使用SIwave可以在IC(U17)芯片電源/地處放置一個端口,計算電路板在適當帶寬內的輸入阻抗。仿真顯示了電路板本身電容的影響而忽略了經過電源的低感應電流回路,由仿真結果可知,阻抗隨著頻率的減少而增加,但由于經過電源的回路存在低阻抗,因此這種關系并不嚴格。
為了使阻抗在1 MHz處低于目標阻抗0.825 Ω,電容值至少為0.18 μF,為此首先需要增加6個30 nF的電容矩陣(ESL=0.5 nH,ELR=0.05 Ω),此時的仿真Z參數如圖5所示。本文引用地址:http://www.j9360.com/article/179002.htm
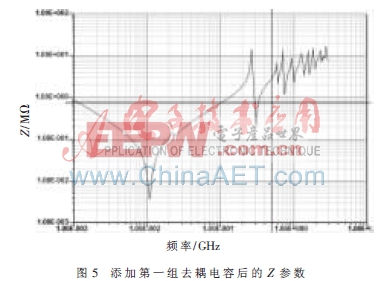
繼續做諧振仿真,板子在f=0.257 GHz處發生諧振,再添加4個10 nF的電容矩陣(ESL=0.3 nH,ELR=0.03 Ω),此時的仿真參數如圖6所示。
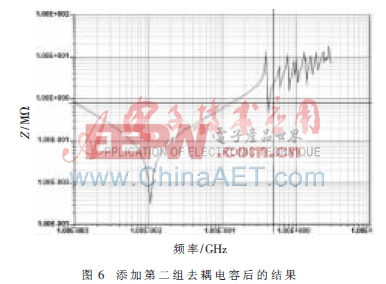
由圖6可知,第一個尖峰值從圖5中的180 MHz變到了圖6中的400 MHz,然后在U17周圍添加4個去耦電容,分別為0.3 nF、1 nF、3 nF、10 nF的電容矩陣(ESL=0.1 nH,ELR=0.01 Ω),為了使仿真與實際情況相符,還在板子最上端添加一個0.1 Ω的VRM等效電阻,此時的仿真Z參數如圖7所示。由圖7可知,添加去耦電容后,電源/地之間的阻抗變得非常小,在500 MHz頻率內,基本低于0.825 Ω。由于容值更小的電容具有更小的ESL和ESR值,因此增加旁路電容的數量有助于提高其高頻特性。

2 采用EBG(高阻抗電磁表面結構)抑制SSN
EBG結構是具有帶阻特性的周期性結構,可以采用金屬、鐵磁或鐵電物質植入基質材料,或者由各種合適材料周期性排列而成。采用EBG結構作為PCB襯底時,跨越幾個EBG周期單元的電路元件將能實現濾波。利用EBG結構可以實現在微帶電路襯底中集成具有很寬阻帶的濾波器,當和其他電路元件有機地結合起來時,可節省電路空間。
采用EBG結構抑制SSN時,特別在高頻時,效果比單純加去耦電容好許多。因為頻率的升高要求加入的去耦電容的數量隨之變多,從而引起其他的一些效應。而采用EBG結構+去耦電容的方式則可以更有效地在更高頻率范圍上提供一個較大的禁帶寬度,在最高頻率下能盡量滿足PDS的最小阻抗要求,從而減小SSN。
本文將對此單純加去耦電容的PDS設計和采用8×8方形EBG結構加去耦電容PDS設計的仿真結果。第一組數據是兩個80 mm×80 mm的平面電路板之間分別加入6×6電容矩陣和9×9電容矩陣,電容為10 nF,忽略其ESL和ESR。分別測試其Z參數。
結果表明6×6電容矩陣在頻率為2 GHz以下其特性阻抗低于7 Ω,9×9電容矩陣在頻率為3.7 GHz以下保持其特性阻抗低于7 Ω。
第二組數據采用前面分析8×8 EBG結構+6×6去耦電容矩陣和8×8改進EBG結構+6×6去耦電容矩陣兩種結構,并仿真得出結果。
結果顯示8×8 EBG+6×6去耦電容矩陣結構可以使特性阻抗在頻率為3.4 GHz以下都保持低于7 Ω,而8×8改進EBG+6×6去耦電容矩陣結構則可以使特性阻抗在頻率為4.2 GHz以下都保持低于7 Ω,結果表明采用EBG結構的PDS設計比傳統單純加去耦電容更具有優勢。
參考文獻
[1] CHEN Guang, KATHLEEN M, JOHN P.The applications of EBG structures in power/ground plane pair SSN suppression[J].IEEE Microwave and Wireless Components Letters, 2004,15(3).
[2] HOWARD J, MARTIN G.High-speed digital design[M]. Prentice Hall PTR, 1993.
[3] BOGATIN E.Signal integrity-simplified[M].Prentice Hall PTR, 2003.
[4] PART M D,PANT P,WILLS D S.On-chip decoupling capacitor optimization using architectural level prediction[J]. IEEE Transactions on Very Large Scale Integration(VLSI) Systems, 2002(2):319-326.
[5] KOZHAYA J N,NASSIF S R,NAJM F N.A multigrid-like technique for power grid analysis[J].IEEE Trans. on CAD of integrated circuits and systems, 2002,21(10):1148-1160.








評論