另外，LC振蕩的幅度對于正激式開關電源和反激式開關電源是不同的。對于正激式開關電源，當電源開關管Q1導通的時候，正好開關變壓器要向負載輸出能量，等效負載電阻R的值相對比較小，即衰減系數很小，LC振蕩回路被阻尼得很厲害，因此，振蕩幅度下降很快，一般第一個振蕩周期過后，振蕩回路很難再次振蕩起來。

對于反激式開關電源，當電源開關管Q1導通的時候，開關變壓器只是存儲能量，沒有能量輸出，因此，等效負載電阻R的值非常大，相當于開路，此時，衰減系數很大，約等于1，即LC振蕩回路基本上沒有被阻尼，LC振蕩是等幅振蕩，其振蕩的幅度基本上等于分布電容Cs兩端電壓的半波平均值Uc ，即：分布電容Cs兩端電壓Uc的最大值Ucm約等于輸入電壓U的兩倍，即：Ucm = 2U，Ucm為分布電容Cs兩端電壓μc 的最高電壓。

當電源開關管Q1關斷瞬間，即t = t6~t7時刻，相當于開關變壓器初級線圈的一端被切斷，開關變壓器中的漏感Ls和分布電容Cs與勵磁電感Lμ的充放電回路基本被切斷，原來存儲于Ls、Cs、Lμ中的能量會生產反電動勢，它只能通過等效負載R和電源開關管的內阻進行釋放。因此，反電動勢的大小與Ls、Cs、Lμ存儲能量的大小有關，還與等效負載R的大小以及電源開關管關斷速度的快慢有關，而 存儲能量又與占空比有關。

我們從(2-135)式以及圖2-44還可以看出，當電源開關管Q1導通時，分布電容Cs兩端電壓μc也是勵磁電感Lμ兩端的電壓，此電壓由一個振蕩波形與一個半波平均值Uc疊加，Uc≈U，因此，在Uc 的作用下，在勵磁電感Lμ中有一個隨著時間增長的線性電流通過，此電流大小為：

上式中，iμ為勵磁電感Lμ中的勵磁電流， Iμm為勵磁電流的最大值; iμ(0)為流勵磁電感Lμ中的初始勵磁電流，即時間t = 0時的勵磁電流， iμ(0)大小與電源開關管的占空比有關，一般當占空比等于或小于0.5時，iμ(0)等于0。

勵磁電感Lμ存儲的能量為：

Wμ=Lμ*I2μm/2 (2-138)

當電源開關管Q1由導通到關斷瞬間，Lμ勵磁電感 存儲的能量會產生反電動勢，反電動勢的大小與電流電感的大小以及電流變化率成正比，即：

eμ=Lμdi/dt(2-139)

(2-139)式中， eμ為勵磁電感Lμ產生的反電動勢， Lμ為勵磁電感的電感量， di/dt為電流變化率，負號表示反電動勢的方向與原來電壓的方向相反。

求解(2-139)式的結果一般都需要解微分方程，這種計算方法我們在第一章中已經反復用過，下面我們另外介紹一種比較簡便的方法，即半波平均值法。

知道了勵磁電感中存儲的能量，在實際應用中，不用解微分方程同樣也可以計算出勵磁電感產生的反電動勢。勵磁電感產生的反電動勢由下式求得：

(2-140)式中， Eμ為勵磁電感Lμ產生的反電動勢(平均值)， Wμ為勵磁電感存儲的能量， toff為電源開關管的關斷時間， RL為等效負載電阻(能量泄放電阻)，它與流過電源開關管電流的大小或內阻也有很大的關系。

值得說明的是，(2-139)式與(2-140)式中的反電動勢在意義上是不同的，(2-139)式中的反電動勢為瞬時值，它一個以時間為自變量按指數規律或正弦規律變化的函數;而(2-140)式中的Eμ為平均值，即半波平均值，相當于把電感產生的反電動勢等效成一個方波。根據歐拉公式，兩個正交指數函數的和正好是一個正弦波，因此，LC諧振電路產生的電壓或電流正好是正弦波。另外，當自由振蕩起振時，其包絡是按指數規律規律增加的，當其產生阻尼振蕩時，其包絡又是按指數規律規律衰減的。

知道了半波平均值，同樣也可以通過它來估算最大值，因為指數函數是變化規律的：當時間t等于τ時(τ為時間常數)，函數值的變化量(上升或下降)是最大值的63%;當時間t等于2.3τ時，函數值的變化量是最大值的90%。另外，正弦函數也是有規律的，因此，只要知道電路的時間常數和工作脈沖的寬度，以及半波平均值，就很容易估算出其最大值或瞬時值。

通過對圖2-44電路進行詳細分析，以及圖2-45對應圖2-44電路中的各點波形，使我們更容易理解半波平均值的意義。半波平均值就是把一個復雜的波形等效成一個方波。對于一個具有一定電工理論基礎的人來說，一般電路中的工作電壓波形基本上是了解的，理解半波平均值的意義之后，很容易就會把一個復雜的波形可以看成是一個已知的正弦波(或指數函數波)在上面進行迭加，這樣可使問題處理變得非常簡單。

從原理上來說，用圖2-44的等效電路來等效開關變壓器的工作原理還是有些過于簡單，因為，在圖2-44中，當電源開關管Q1突然關斷瞬間，分布電感Ls沒有放電回路，即負載電阻為無限大，根據(2-140)式，分布電感Ls兩端產生的反電動勢將非常大;但實際上，在分布電感 產生反電動勢的時候，它是可以通過分布電感兩端的分布電容產生并聯振蕩的，因此，我們可以把圖2-44電路進一步改進成如圖2-46所示電路。

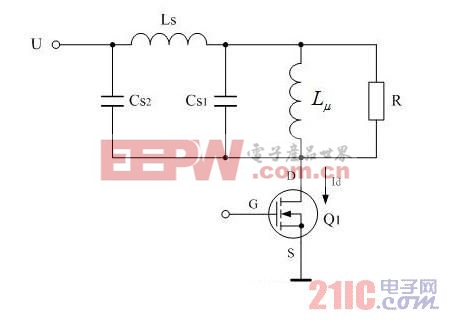
在圖2-46中，Cs1、Cs2都是分布電容，它們對于分布電感 來說，既可以產生串聯振蕩，又可以產生并聯振蕩。在電源開關管Q1導通瞬間，分布電感與分布電容主要是產生串聯振蕩，因為輸入電壓開始向串聯振蕩回路提供能量;在電源開關管Q1關斷瞬間，分布電感與分布電容主要是產生并聯振蕩，因為分布電感Ls必須要通過并聯回路釋放能量。在實際應用中，分布電感Ls相對于勵磁電感Lμ來說很小，因此，如果不考慮分布電感Ls 的作用，完全可以把Cs1、Cs2看成是一個分布電容。

由于在變壓器線圈中，分布電容和分布電感是由非常多的電容和分布電感互相串、并聯在一起組成，如要嚴格地用集中參數完全把它們等效是很難的。至于等效電路是采用串聯還是并聯，這主要看它在電路中所起的關鍵作用。例如，在電源開關管接通時，串聯電容的作用是主要的;而在電源開關管關斷時，并聯電容的作用反而是主要的。

當電源開關管Q1關斷瞬間，分布電感Ls產生反電動勢將會在分布電感 、Cs1、Cs2組成的LC回路中產生并聯振蕩，并聯振蕩回路電容由Cs1和Cs2串聯而成，Cs1和Cs2的大小以及比例關系，與變壓器線圈的結構有關，線圈的層數越多，串聯電容的容量就越大。

從圖2-45-c以及(2-140)式還可以看出，分布電感Ls以及勵磁電感Lμ產生的反電動勢，其幅度一般都等于或大于輸入電源電壓的幅度(假設占空比等于0.5)，即加到電源開關管D極的電壓最高可達輸入電壓的兩倍以上。這是因為電源開關管的關斷時間一般都很短，而分布電感釋放能量時等效負載電阻很大的緣故。因此，如果不對電源開關管采取保護措施，反電動勢很容易就把電源開關管擊穿。

根據(2-140)式，降低分布電感反電動勢幅度的最有效方法是減小負載電阻RL的阻值。除此之外，還可以在諧振回路接入一個由電阻、電容并聯，然后與整流二極管串聯的反電動勢限幅電路，來對分布電感以及勵磁電感產生的反電動勢進行限幅，如圖2-47所示。

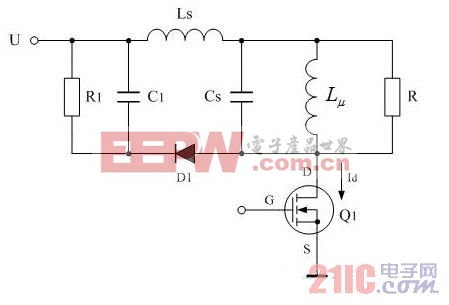
圖2-47 對分布電感以及勵磁電感產生的反電動勢進行限幅

在圖2-47中，當電容器C1充上一定的電荷之后，其作用就相當于一個穩壓二極管，不過這個穩壓二極管的穩定電壓值是動態的，它會隨著反電動勢的幅度升高而升高，而整流二極管D1的作用就相當于一個限幅二極管。當反電動勢的幅度高于電容器C1兩端的電壓時，整流二極管D1就導通，反電動勢就會向電容器C1充電，使變壓器初級線圈的分布電感存儲的能量向電容器轉移，從而起到降低反電動勢幅度的作用，與此同時電阻R1也會吸收一部份能量，使反電動勢的幅度進一步降低。

電容器C1在吸收反電動勢能量的過程中，其兩端電壓也會提高，但它可以通過R1進行放電，使電容器兩端的電壓基本保持在一個合理的范圍。即：電容器C1在吸收反電動勢的能量是有條件的，只有反電動勢的的幅度超過某個值之后，它才開始吸收。正確選擇RC放電的時間常數，使電容器在下次充電時的剩余電壓剛好略高于方波電壓的幅度，而電容充滿電的幅度又低于開關管的耐壓幅度，此時電源的工作效率最高。

以上我們對開關變壓器的工作原理做了的比較詳細的分析，但對于要設計一個實際電路中使用開關變壓器來說，上面這些這些知識還遠遠不夠，因此，后面我們還會用很大的篇幅來對開關變壓器參數設計加以說明。因為，在具體電路中各種開關變壓器的技術要求或參數都是不一樣的，更多的內容留待我們后面進行具體電路設計時再詳細介紹。