定點DSP中高精度除法的實現方法
引 言
本文引用地址:http://www.j9360.com/article/170751.htm各種集成化單片數字信號處理器(DSP)以其功能強、集成度高、應用靈活、性價比高等優點,在信號處理和系統控制中的主導性地位日益明顯。許多信號處理和控制需要運用除法運算。一般的數字信號處理器中沒有現成的除法指令。十多年前誕生的浮點DSP,由于其用硬件完成浮點數的運算,在數據處理和運算能力上大大超出定點DSP,處理除法運算也比定點DSP更為簡單。但是定點DSP每器件產品的價格更低,這對大規模的大眾市場應用而言是相當重要的優勢,也是定點器件至今仍是業界主流的主要原因。所以,討論定點DSP中除法的實現仍不失其意義。在定點DSP中雖然已經有人給出除法的算法,但是由于其運算的復雜和精度難以如愿,致使一些帶有除法的好的算法在信號處理中難以得到應用。
為了提高運算結果的精度,本文在已有除法算法的基礎上進行了一些改進,最大限度地保證了結果的精度。最后在TI公司的TMS320C5416芯片里具體實現并驗證了這一高精度除法。
1 經典算法
DSP中沒有現成的除法指令,除法是靠被除數與除數之間的移位相減來實現的。在C54X系列里利用減法指令SUBC和循環指令RPT實現2個16位數的相除。下面以C54X為例來具體實現經典的除法:
C54X提供的SuBC指令僅對無符號數進行操作,所以在移位相減開始之前必須先將被除數和除數取絕對值,僅考慮2個正數的除法。此時除法運算有兩種情況:
當|被除數||除數|時,將|被除數|存放在累加器的高16位,然后用SUBC完成15次移位相減,相減之后在累加器A的低16位中存放商的絕對值。根據運算前被除數和除數的符號是否相同來決定是否要改變所得結果的符號。
當|被除數|≥|除數|時,將|被除數|存放在累加器的低16位,然后用SUBC完成16次移位相減,相減之后在累加器A的低16位中存放商的絕對值。根據運算前被除數和除數的符號是否相同來決定是否要改變所得結果的符號。
從實現的過程分析,當|被除數||除數|時,移位相減開始時|被除數|和|除數|的小數點位置正好相差一位。第一次相減后在累加器A的O位最低位存進的數值正是商的最高位,該位為商的小數點后第一位。在15次移位相減之后,累加器A低16位所得的結果為Q值為15的小數。當|被除數|≥|除數|時,在第l6次相減時,|被除數|位于A的高16位(30~15位)上,小數點位在A的15位后,和|除數|的小數點位正好對齊,則此次相減后在A的0位加上的值正好是商的最低有效整數位,相當于十進制數中的個位。所以在16次移位相減之后,累加器A低16位所得的結果為Q值為0的整數。以此分析,當商的精確值不是整數,或者超出Q值15所表示的范圍時,此算法所得結果就達不到16位數據所能表達的精確度。
表1中任取幾組數據來說明。
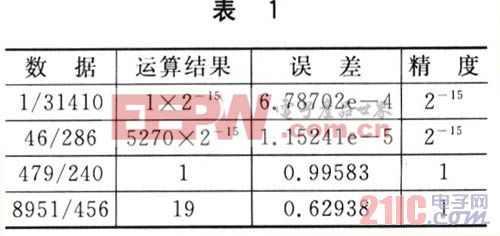













評論