永磁同步發電機的預測直接轉矩控制
摘要:針對直接轉矩控制(DTC)數字控制系統采樣與控制時延所造成的電機轉矩與磁鏈紋波增大的問題,提出一種應用于永磁同步發電機(PM SG)的預測DTC策略。通過建立PMSG的數學模型,深入分析控制系統的時延機理,建立了基于電機模型方程的轉矩與磁鏈預測算法。最后構建了PMSG實驗機組,實驗結果表明,該預測策略在保持傳統DTC優良動態性能的基礎上,可有效減小轉矩紋波,系統性能得到提升。
關鍵詞:永磁同步發電機;直接轉矩控制;時間延遲
1 引言
以風力發電為代表的可再生能源得到廣泛關注,其中基于雙饋感應發電機與PMSG的風電系統應用最為廣泛。由于PMSG風電系統具有運行
效率高、調速范圍寬等優點,且無需齒輪箱、滑環與電刷等,已成為大功率、海上風電領域極具潛力的發展方向。
為滿足PMSG的高性能運行需求,DTC作為一種先進的交流電機控制策略,應用于風電領域極具優勢。其中基于空間矢量調制(SVM)的DTC具有開關頻率恒定、轉矩紋波較小等優點。為改善傳統DTC較大的轉矩與磁鏈紋波,可采用基于開關表方法的預測DTC技術,但其控制算法較復雜,且無法克服開關頻率不固定等問題。
為提高PMSG運行性能,在此建立PMSG數學模型,在分析控制系統采樣延遲的基礎上,提出一種基于SVM的預測DTC策略。通過搭建的PMSG實驗機組,對所提方案進行了實驗驗證。
2 PMSG預測直接轉矩控制
2.1 PMSG數學模型
兩相靜止α,β坐標系下PMSG的定子電壓、磁鏈數學模型為:

2.2 預測直接轉矩控制策略
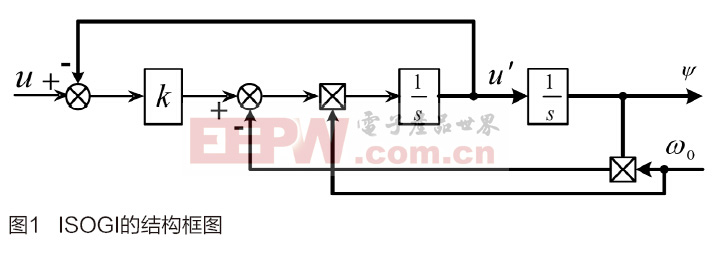
傳統DTC算法中,定子磁鏈與電磁轉矩是根據當前采樣點(假定為k時刻)的電壓u(k)與電流值i(k)由式(1),(2)算得,并根據DTC策略得到相應的目標電壓矢量v(k)。理想情況下該電壓矢量在k時刻施加,在k+1時刻使轉矩與磁鏈達到給定值,如圖1a所示。但由于采樣及數字計算的延遲,期望電壓矢量實際上是在一個采樣周期后,即k+1時刻施加,在k+2時刻才使轉矩與磁鏈達到給定值,如圖1b所示。這使得轉矩與磁鏈的響應始終滯后一個開關周期,降低了PMSG系統的運行性能。
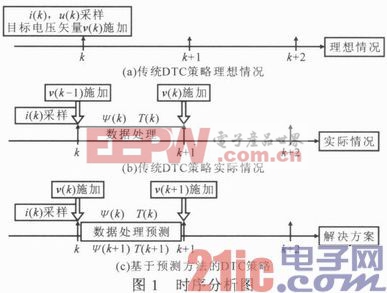
對此,這里給出一種基于預測方法的DTC策略,如圖1c所示。根據k采樣時刻電壓電流值計算出定子磁鏈與轉矩值,根據PMSG模型對k+1時刻的磁鏈與轉矩值進行預測,進而選出合適的電壓矢量。這樣在k+1時刻,施加的電壓矢量為v(k+1),當k+2時刻到來時,使得k+2時刻的磁鏈與轉矩值剛好達到給定,以解決由于時間延遲帶來的轉矩與磁鏈紋波較大等問題。
2.3 預測算法
為改善由于時間延遲導致PMSG運行性能下降的問題,需在DTC中加入對轉矩和磁鏈的預測。由式(1)可得定子磁鏈的預測表達式為:

若能推導出isα(k+1)與isβ(k+1),根據式(2)便可得到k+1時刻的轉矩值,但由于所研究的PMSG為凸極電機,難以在α,β軸下求解電流值,鑒于此可在d,q旋轉坐標系下對電流進行預測。
PMSG在d,q旋轉坐標系下的電壓方程為:

根據式(5)可預測k+1時刻的電流值,然后對其進行反Park變換(變換時需要轉子位置信息θ,θ值由無位置傳感器獲得),即可得到α,β軸
下電流的預測值,結合式(2),(3)即可計算出k+1時刻的轉矩預測值:
Te(k+1)=3np[ψsα(k+1)isβ(k+1)-ψsβ(k+1)isα(k+1)]/2 (6)



















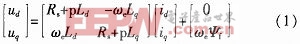
評論