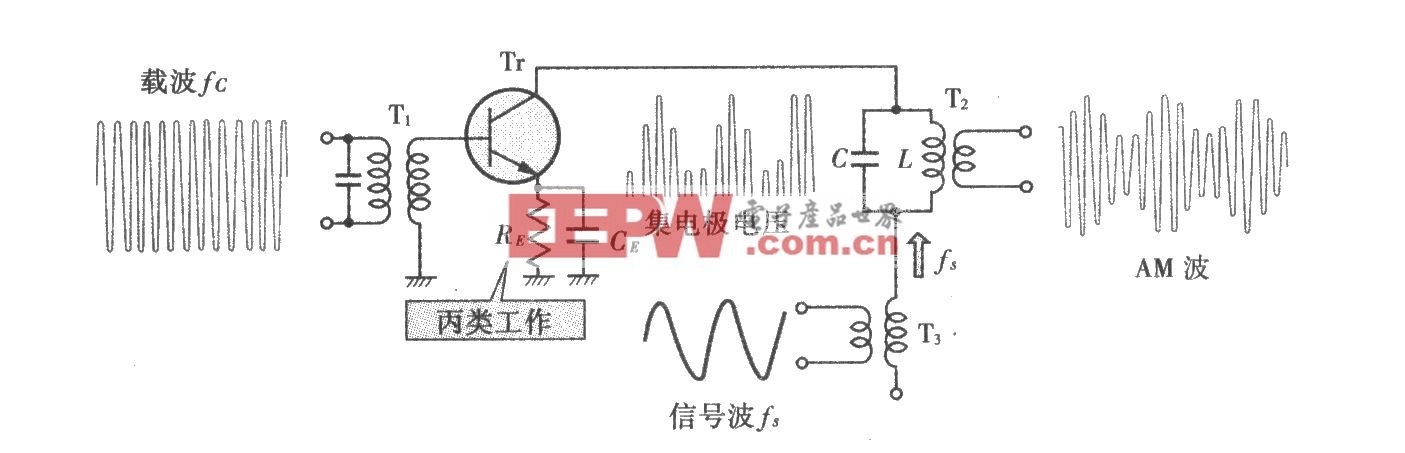
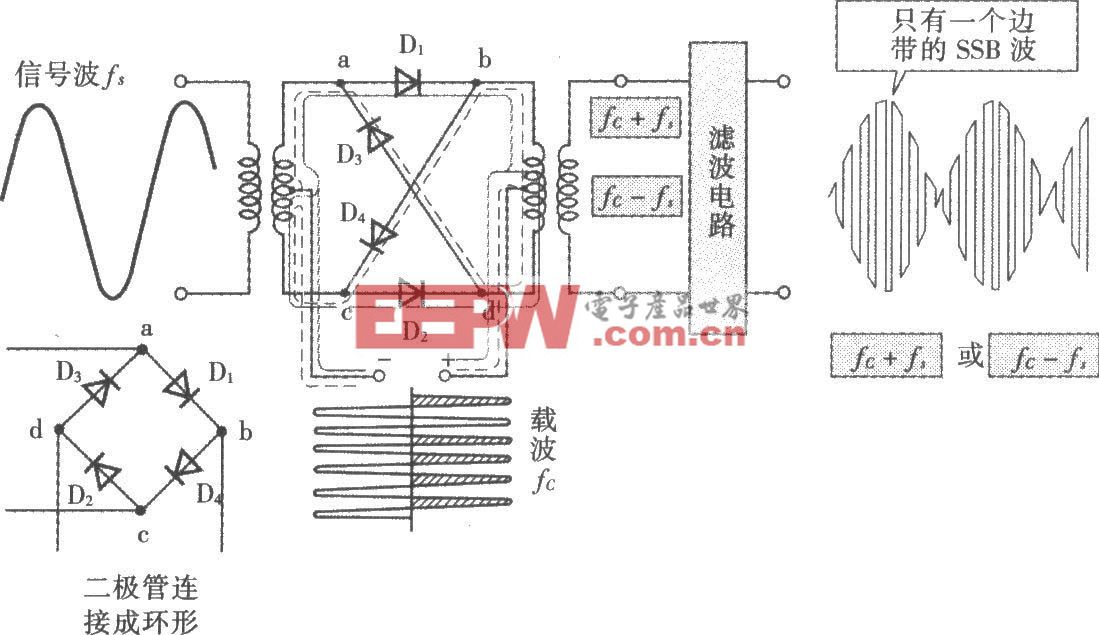
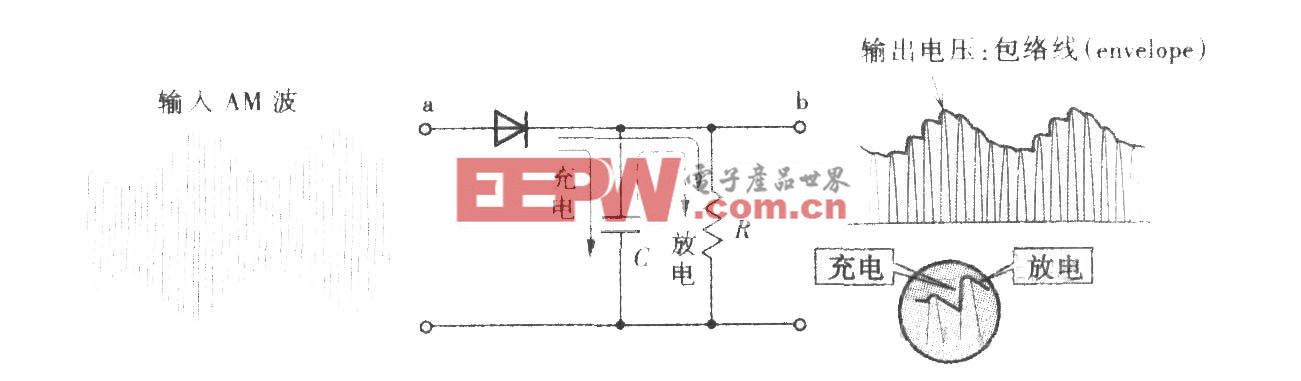
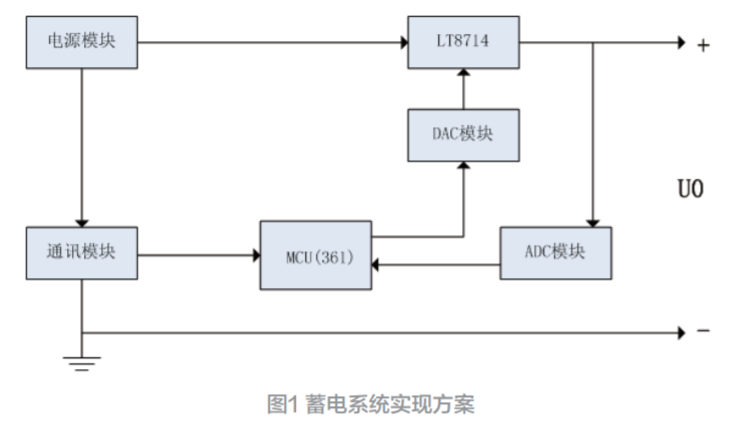
電路基礎系列:交流電路篇-11 串聯諧振電路
當電源頻率使L和C兩端的電壓相等或相反時,串聯電路就會發生共振
到目前為止,我們已經分析了源電壓為固定頻率穩態正弦電源的串聯RLC電路的行為。我們也看到了在我們的教程關于串聯RLC電路,兩個或更多的正弦信號可以使用相量組合,只要他們有相同的頻率供應。
但是,如果在電路上施加一個固定振幅但頻率不同的電源電壓,電路的特性會發生什么變化。另外,由于頻率的變化,電路的“頻率響應”行為會對兩個無功元件產生什么影響。
在串聯RLC電路中,當電感的電感電抗與電容的電容電抗相等時,就會出現一個頻率點。換句話說,XL= XC. 發生這種情況的點稱為共振頻率點(Er)當我們分析一個串聯RLC電路時,這個共振頻率產生了一個串聯諧振 .
串聯諧振電路是電子電路中最重要的電路之一。它們以各種形式存在,例如交流電源濾波器、噪聲濾波器以及無線電和電視調諧電路中,產生用于接收不同頻率信道的非常有選擇性的調諧電路。考慮下面的簡單串聯RLC電路。
串聯RLC電路
首先,讓我們定義一下我們已經知道的串聯RLC電路。
根據上述感應電抗方程式,如果頻率或者電感當電感器的總電感電抗值增加時,電感器的電抗值也會增加。當頻率接近無窮大時,電感器的電抗也會隨著電路元件的開路而增加到無窮大。
然而,當頻率接近于零或直流時,電感器的電抗會降到零,造成相反的效應,就像短路一樣。這意味著,感應電抗為鈥比例“到頻率,低頻時小,高頻時高,這在下面的曲線中得到了證明:
頻率感應電抗
感應電抗與頻率的關系圖是一條直線線性曲線。電感器的感應電抗值隨頻率的增加而線性增加。因此,感應電抗為正,與頻率成正比(十我E )
上面的容性電抗公式也是如此,但反過來。如果頻率或者電容增加總電容電抗會降低。當頻率接近無窮大時,電容器的電抗將降到幾乎為零,從而使電路元件起到0Ω的完美導體的作用。
但是當頻率接近于零或直流電平時,電容器的電抗會迅速增加到無窮大,使其表現為一個非常大的電阻,變得更像是開路狀態。這意味著電容電抗為鈥反比例“任何給定電容值的頻率,如下所示:
頻率容抗
電容電抗對頻率的關系曲線為雙曲線。電容器的電抗值在低頻時有很高的值,但隨著頻率的增加迅速減小。因此,電容電抗為負,與頻率成反比(XC E -1 )
我們可以看出這些電阻的值取決于電源的頻率。以更高的頻率XL頻率很高,頻率很低XC很高。那么一定有一個頻率點的值XL與的值相同XC還有。如果我們現在把感性電抗曲線放在電容電抗曲線的上面,使兩條曲線在同一軸線上,交點將給出串聯諧振頻率點(Er或 or)如下所示
串聯諧振頻率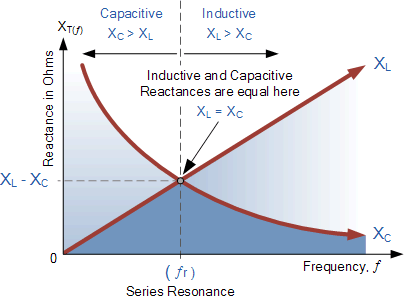
式中:fr以赫茲表示,L以亨利表示,C以法拉表示。
交流電路中,當兩個電抗相反且相等的電抗相互抵消時,就會發生電諧振XL= XC在圖上發生這種情況的點是兩條電抗曲線互相交叉。在串聯諧振電路中,諧振頻率,fr點可以計算如下
我們可以看到,在共振時,兩個電抗互相抵消,從而使串聯LC組合起到短路的作用,串聯諧振電路中唯一與電流流動相反的就是電阻,R. 在復數形式下,諧振頻率是串聯RLC電路的總阻抗變為純阻抗的頻率 "Real",這不是虛阻抗的存在。這是因為共振時它們被抵消了。所以串聯電路的總阻抗變成了電阻值,因此:Z = R .
然后在共振時,串聯電路的阻抗為最小值,僅等于電阻,R電路的。共振時的電路阻抗稱為電路的“動態阻抗”,取決于頻率,十C(通常為高頻)或十我(通常在低頻下)將控制共振的任一側,如下所示。
串聯諧振電路中的阻抗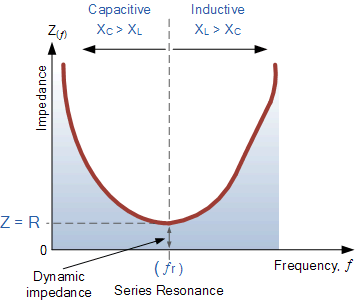
注意,當電容電抗控制電路時,阻抗曲線本身具有雙曲線形狀,但當電感電抗控制電路時,由于十我 .
你也可以注意到,如果電路阻抗在共振時是最小的,那么電路導納串聯諧振電路的一個特點是導納非常高。但這可能是一件壞事,因為諧振時的電阻值很低,意味著流經電路的電流可能高得危險。
我們記得上一篇關于串聯RLC電路的教程,串聯組合的電壓是相量和五R ,五我和五C. 如果在共振時,兩個電抗相等且相消,則兩個電壓代表五我和五C也必須是相反的和相等的值,從而相互抵消,因為純元件的相量電壓是90o和-90o分別
然后在共振級數電路組件五我= -VC零電壓和電阻之間的電壓都會下降。因此,五R= V供給正是因為這個原因,串聯諧振電路被稱為電壓諧振電路(而不是電流諧振電路的并聯諧振電路)。
串聯諧振RLC電路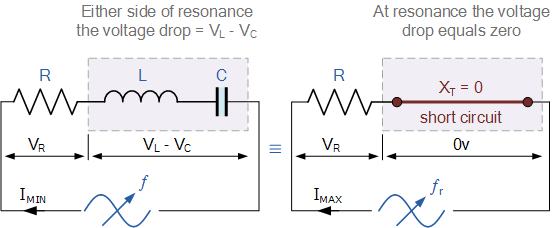
由于流過串聯諧振電路的電流是電壓除以阻抗的乘積,在諧振時阻抗為,Z處于最小值(=R). 因此,此頻率下的電路電流將處于其最大值垂直/反向如下所示
串聯電路諧振電流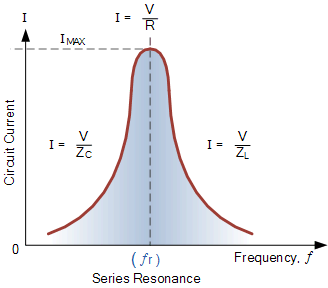
串聯諧振電路的頻率響應曲線表明電流的大小是頻率的函數,并將其繪制到圖表上,可以看出響應從接近零開始,在諧振頻率達到最大值我馬克斯= IR然后又降到接近零E變得無限。其結果是通過感應器的電壓大小,我還有電容器,C即使在共振時,也會比電源電壓大很多倍,但當它們相等且相反時,它們相互抵消。
由于串聯諧振電路只在諧振頻率上起作用,這種電路又稱為串聯諧振電路受主電路因為在共振時,電路的阻抗處于最小值,所以很容易接受頻率等于其諧振頻率的電流。
您可能還注意到,由于諧振時通過電路的最大電流僅受電阻值(純值和實值)的限制,因此電源電壓和電路電流必須在該頻率下彼此同相。那么串聯諧振電路的電壓和電流之間的相位角也是固定電源電壓的頻率函數,在諧振頻率點為零,當:五、 我和五R如下圖所示。因此,如果相角為零,那么功率因數必須是統一的。
串聯諧振電路的相角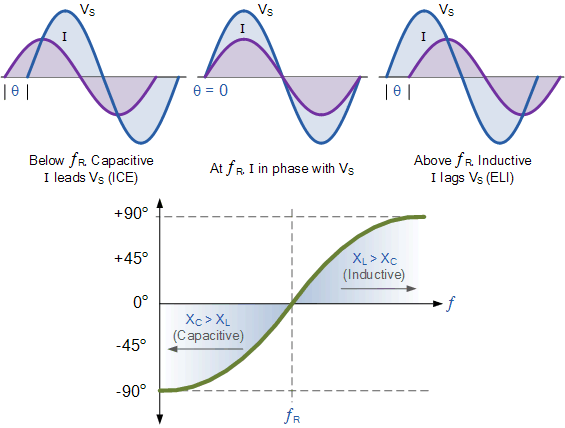
還要注意,相位角對于上述頻率是正的Er頻率低于Er這可以證明,
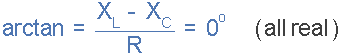
如果串聯RLC電路由恒壓下的變頻驅動,則電流的大小,我與阻抗成正比,Z因此,在共振時,電路吸收的功率必須達到其最大值,如P = I^2*Z .
如果我們把共振頻率的兩個點增加,我們稱之為共振頻率的一半半功率點比最大值低-3dB,取0dB作為最大電流基準。
這些-3dB點給出的電流值是其最大諧振值的70.7%,其定義為:0.5(I2R)=(0.707 x I)2R。那么在一半功率下對應于較低頻率的點稱為“較低截止頻率”,標記為?L,與半功率時的上頻率對應的點稱為“上截止頻率”,標記為?H。這兩點之間的距離,即(?H–?L)稱為帶寬(BW),是提供至少一半最大功率和電流的頻率范圍,如圖所示。
串聯諧振電路的帶寬以上電路電流幅值的頻率響應與串聯諧振電路中諧振的“銳度”有關。峰的銳度是定量測量的,稱為品質因數,Q電路的。品質因數將儲存在電路中的最大或峰值能量(電抗)與每個振蕩周期中消耗的能量(電阻)相關聯,這意味著它是諧振頻率與帶寬的比值,并且電路越高問帶寬越小,Q = ?r/體重 .
當帶寬在兩個-3dB點之間時選擇性電路的一個度量是它拒絕這些點任一側任何頻率的能力。一個更具選擇性的電路將具有較窄的帶寬,而較低選擇性的電路將具有更寬的帶寬。串聯諧振電路的選擇性可以通過調節電阻值來控制,同時保持所有其他元件不變,因為Q = (X我或者XC)/R .
串聯RLC諧振電路的帶寬然后將串聯諧振電路的諧振、帶寬、選擇性和品質因數之間的關系定義為:
1) 共振頻率(fr )
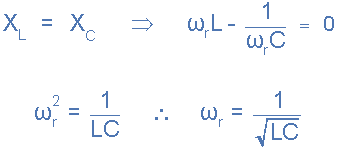
2) 電流(I)
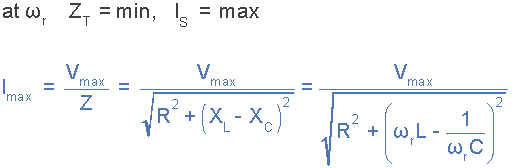
3) 下限截止頻率(?L)
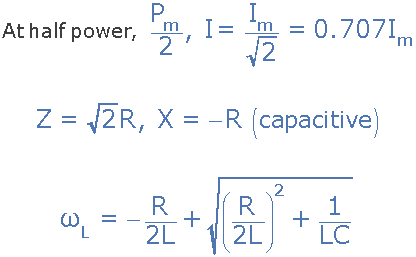
4)上限截止頻率(?H)
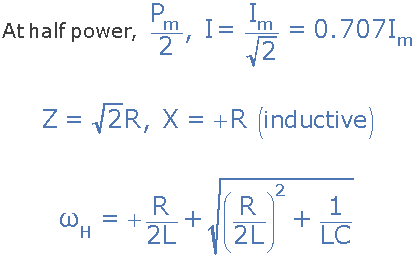
5) 帶寬(BW)
6) 質量系數(Q)
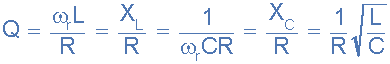
串聯諧振網絡由一個30Ω的電阻器、一個2uF的電容器和一個20mH的電感器組成,通過一個在所有頻率下恒定輸出9伏的正弦電源電壓連接。計算諧振頻率,諧振電流,諧振時電感和電容的電壓,電路的品質因數和帶寬。同時繪制所有頻率對應的電流波形。
1共振頻率,fr

2諧振時的電路電流,I

三。共振時的感應電抗,XL

4電感器和電容器之間的電壓,VL,VC
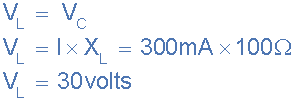
注:電源電壓可能只有9伏,但在諧振時,電容器上的無功電壓,VC還有電感器,V我峰值是30伏!
5質量因素,Q
6帶寬,BW
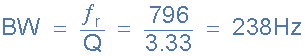
7上下-3dB頻率點,fH和fL
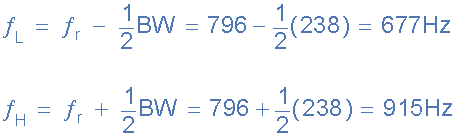
8電流波形
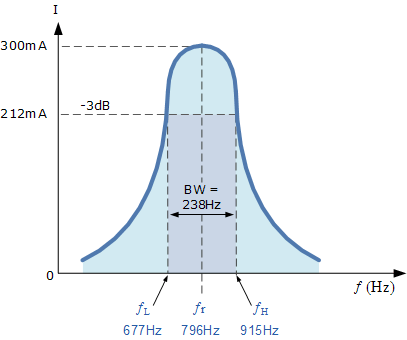
串聯電路由一個4Ω的電阻、500毫安時的電感和一個連接在100V、50Hz電源上的可變電容組成。計算產生串聯諧振條件所需的電容,以及在諧振點通過電感器和電容器產生的電壓。
共振頻率,Er
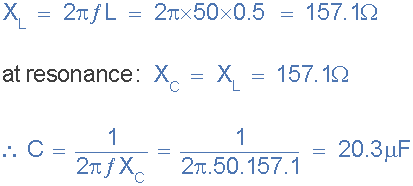
電感器和電容器之間的電壓,五我,伏C

您可能已經注意到,在本教程中分析串聯諧振電路時,我們研究了帶寬、上下頻率、-3dB點和質量或Q系數。所有這些都是用于設計和建造帶通濾波器(BPF)的術語,事實上,諧振電路用于3元件主濾波器設計,以通過“通帶”范圍內的所有頻率,同時拒絕所有其他頻率。
然而,本教程的主要目的是分析和理解串聯諧振發生在無源RLC串聯電路中。它們在RLC濾波器網絡和設計中的使用超出了本教程的范圍,因此這里將不再討論,抱歉。
為了在任何電路中發生共振,它必須至少有一個電感器和一個電容器。
諧振是當儲存的能量從電感器傳遞到電容器時電路中振蕩的結果。
當XL=XC且傳遞函數的虛部為零時發生共振。
諧振時,電路的阻抗等于電阻值Z=R。
在低頻時,串聯電路是電容性的,如:XC>XL,這使電路具有超前功率因數。
在高頻時,串聯電路是感應式的,如:XL>XC,這給了電路一個滯后功率因數。
諧振時的高電流值在電感和電容上產生非常高的電壓值。
串聯諧振電路可用于構造高頻率選擇性濾波器。但是,其高電流和極高的元件電壓值可能會損壞電路。
諧振電路的頻率響應最顯著的特征是其振幅特性有一個尖銳的諧振峰。
因為阻抗最小,電流最大,所以串聯諧振電路也被稱為接收器電路。.
在下一個關于并聯諧振的教程中,我們將研究頻率如何影響并聯RLC電路的特性,以及此時并聯諧振電路的Q因數如何決定其電流放大倍數。
*博客內容為網友個人發布,僅代表博主個人觀點,如有侵權請聯系工作人員刪除。