利用矢量旋轉求解平方根的算法及其FPGA實現*
引言
本文引用地址:http://www.j9360.com/article/96987.htm隨著電子技術的不斷發展,EDA技術在數字信號處理領域得到了越來越多的應用。在FPGA中,應用VHDL語言可以進行加法、減法、乘法等運算,但卻不能直接進行開平方運算。傳統的開平方算法主要可以分為三大類:牛頓迭代法[1~3],SRT-冗余算法[4~5],非冗余算法[6~7]。
當直接利用牛頓迭代法進行開平方運算時,涉及到復雜的除法運算。為了避免除法運算,必須首先計算出平方根的倒數,再與被開方數相乘得到平方根。利用牛頓迭代法求根的迭代次數只和初始值與被開方數之間的誤差有關,而與被開方數無關。另外,運算中還涉及到查表運算,要使迭代次數降低,必須相應地增加查找表的大小。而且在每次迭代運算中都涉及到乘法、加/減法運算,為了提高乘法運算速度,經常通過采用高速并行乘法器和進位保留加法器來輔助運算,需要較高資源。
經典SRT-冗余算法也是基于迭代實現的,在每次迭代中都涉及到加法、乘法、條件判斷轉移、數值轉換等運算,為了減少電路的復雜度,所有的迭代運算都共用硬件資源,因此,該算法的效率較低。
非冗余算法可分為恢復余數的算法和不恢復余數的算法。與SRT算法相似,這兩種算法都需要復雜的迭代運算。恢復余數的算法由于存在反饋補償機制,存在很大延時,效率低;不恢復余數的算法[9]還要采用更多加法運算。
本文提出了一種基于矢量旋轉求三角函數進而求得任意數平方根的算法,并用VHDL語言在Altera EP2S60開發板上加以實現。該算法相比其他傳統開平方算法具有處理速度更快、計算誤差更小、占用資源更少的顯著優勢。
基于矢量旋轉(VR)算法實現開平方的算法
矢量旋轉算法簡介
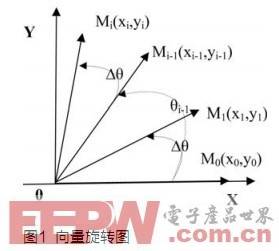
如圖1所示,初始向量M0(x0,y0)與x軸重合,經逆時針旋轉Dq角度之后得到向量M1(x1,y1),依此類推,逆時針旋轉i次之后得到向量Mi(xi,yi)。













評論