在本文的第三部分中，我們將介紹開發嵌入式音頻應用的一些策略。我們將從描述音頻處理中使用的一些標準方法開始，然后討論一些基本的音頻算法。

音頻處理方法

把數據送入處理器內核

　　把數據送入處理器內核有若干種方法。例如，一個前臺程序可以對一個串行端口中的新數據進行查詢，但這種傳輸方式在嵌入式媒體處理器中是不常用的，因為這樣會降低內核的使用效率。

　　取而代之的是，與音頻編解碼器相連的處理器一般用DMA引擎把數據從編解碼器的數據口(就像一個串行口)傳輸到處理器可用的某個存儲空間內。這種數據傳輸是以后臺操作的形式完成的，無需處理器內核的干預。這里的唯一開銷是對DMA序列的設定以及一旦數據緩沖區的接收或發送完成之后對中斷的處理。

塊處理與樣點處理

　　樣點處理和塊處理是處理數字音頻數據的兩種方法。在樣點處理的方法中，只要樣點一出現，處理器就處理這個樣點。這里，在每個采樣周期中的處理操作都會有開銷。許多濾波器(例如FIR和IIR，將在下面敘述)是以這樣的方式實現的，因為這種方式的有效延遲會很低。

　　另一方面，塊處理是基于把數據傳送到處理函數之前對特定長度緩沖區的填充。有些濾波器是用塊處理的方式實現的，因為這樣比樣點處理方式更有效。其中要說明的一點是，塊處理方法大大降低了針對每個樣點而調用處理函數的開銷。而且，許多嵌入式處理器包含有多個ALU， 可以對數據塊進行并行操作。另外，有些算法從本質上就是以塊處理方式操作的。其中一個大家都知道的是傅里葉變換(以及它的實際使用的形式，快速傅里葉變換，或稱FFT)，這種算法接受時域數據塊或空間域(spatial)數據塊，然后把這些數據塊轉換成頻域表示。

雙緩沖

　　在基于塊處理的、使用DMA與處理器內核進行數據傳遞的系統中，必須使用雙緩沖，以便在DMA傳輸和內核之間進行仲裁。這會使處理器內核和獨立于內核的DMA引擎不會在同一時間對同一數據進行訪問，避免了數據一致性問題。為了對長度為N的緩沖區的處理進行改進，我們簡單地產生一個長度為2×N的緩沖區。對于一個雙向系統，必須生成兩個長度為2×N的緩沖區。如圖1a中所示，處理器內核正在對in1緩沖區進行處理，并將結果存儲在out1緩沖區中，而DMA引擎此時正在對in0進行填充，并對out0中的數據進行傳輸。圖1b指出，一旦DMA引擎完成對雙緩沖區左邊半個的操作之后，它就開始把數據傳送到in1，并從out1取出數據，而此時的處理器內核正在處理來自in0的數據，并填入out0。這個結構有時被稱為“乒乓式緩沖”，因為處理器內核來回地對雙緩沖區的左右兩半進行處理。

　　應該注意到，在實時系統中，串行端口的DMA(或者另一個與音頻采樣率關聯的外圍設備的DMA)規定了時序預算。基于這個原因，塊處理算法必須以這樣的方式進行優化，即它的執行時間要小于或等于DMA對雙緩沖區的一半進行數據傳輸所需的時間。

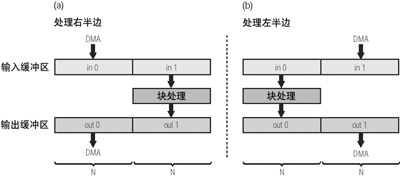
圖1  用于流處理的雙緩沖結構

二維(2D)DMA

　　當數據通過像I2S這樣的數據鏈路傳輸時，它可能會包含多個聲道。這些聲道可以全是從一條數據線上通過復用而輸入到同一個串行端口的。在這種情況下，2D DMA可以用來對數據進行解交織，從而使每個聲道在存儲器中是線性分配的。可以看一下圖2中對這一安排的圖示，其中從左右聲道來的樣點被解復用到兩個分離的數據塊。這個自動數據安排對于那些使用塊處理的系統是極其有用的。

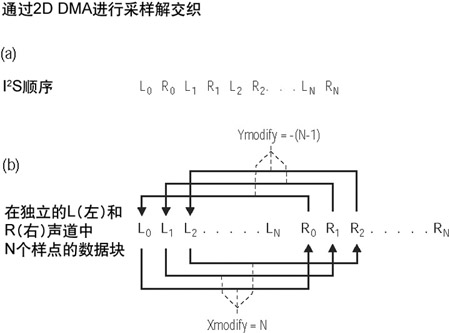
圖2  2D DMA引擎用于解交織  (a) I2S立體聲數據輸入 (b)分離的左右緩沖區

基本操作

　　在音頻處理中有三個基本的構建模塊。它們是加法操作、乘法操作和時間延遲。許多更復雜的效果和算法可以用這三個基本操作來實現。加法器顯而易見的任務是把兩個信號加在一起。乘法可以用于提升或衰減音頻信號。在大多數媒體處理器中，可以在一個周期內完成多次加法和乘法操作。

　　時間延遲有點復雜。在許多音頻算法中，當前的輸出取決于過去的輸入和輸出之間的組合。這種延遲效果是用延遲線實現的，而延遲線只不過是存儲器中用來保持過去數據的一個數組。例如，一個回聲算法可以對每個聲道保持500 mS的輸入樣點。當前輸出值可以用當前輸入值與稍微衰減的過去樣點進行相加后得到。如果音頻系統是基于樣點的處理方式，那么程序設計人員可以簡單地跟蹤一個輸入指針和一個輸出指針(兩者之間保持500 mS樣點數的間隔)，并且在每個采樣周期之后增加這兩個指針。

　　由于延遲線要被隨后的各組數據重復使用，因此，輸入與輸出指針將需要從延遲線緩沖區的末尾回繞到起始端。在C/C++中，這通常是在指針增加操作時再附帶一次求模操作(%)完成的。

　　對于那些支持循環緩沖(見圖3)的處理器來說，這個回繞操作不會增加額外的處理周期。在這種情況下，一個循環緩沖區的起始位置和長度必須只提供一次。在處理過程中，軟件增加或減少緩沖區內的當前指針，如果當前的指針位置落在緩沖區的兩個端點之外，則由硬件使指針回繞到緩沖區的起始位置。如果沒有這個自動地址生成功能，程序設計人員就必須手動地保持對緩沖區的跟蹤，因而會浪費有用的處理周期。

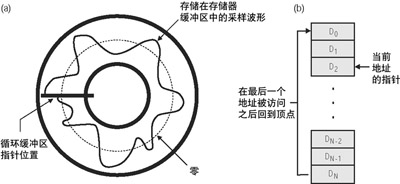
圖3 (a) 使用循環緩沖區的延遲線的圖示 (b) 循環緩沖區在存儲器中的布局

　　由延遲線結構可以引出一個叫做梳狀濾波器的重要的音頻構建模塊，它本質上是一個帶有反饋的延遲線。當多個梳狀濾波器同時使用的時候，可以產生混響的效果。

信號的產生

　　在有些音頻系統中，也許需要合成一個信號(例如一個正弦波)。泰勒級數的函數近似法可以用來對三角函數進行仿真。而且，用均勻隨機數發生器來產生白噪聲是很容易的。

　　但是，合成的方法也許并不適用于某些給定系統的處理預算。在具有充足存儲器的定點系統中，您可以取而代之地使用查表的方法來產生信號。這樣做的負面效應是占用了寶貴的存儲器資源，所以，作為一種折衷考慮，可以使用混合的方法。例如，您可以存儲一個不太精細的函數表，以節省存儲器。在運行時，準確的值可以用插值的方法從函數表中提取出來，而插值操作比使用泰勒級數近似法的時間大為縮短。這個混合法提供了在計算時間和存儲器資源之間的很好的平衡。

濾波與算法

　　音頻系統中的數字濾波器被用來對指定頻帶內的聲波能量進行衰減或提升。最常用的濾波器形式是高通、低通、帶通和點阻。這些濾波器中的任何一種都有兩種實現方法。這就是有限沖擊響應(FIR)濾波器和無限沖擊響應(IIR)濾波器，而且它們組成了搭建像參數均衡器和圖示均衡器那樣更復雜的濾波算法的構建模塊。

有限沖擊響應(FIR)濾波器

　　FIR濾波器的輸出是由當前和過去輸入之和確定的，而其中的每個輸入樣點首先要乘以一個濾波器系數。示于圖4a中的FIR求和公式，也叫做“卷積”，是信號處理中最重要的操作之一。在這個公式的句法中，x為輸入向量，y為輸出向量，而h為濾波器系數。圖4a表示了FIR的實現結構圖。

　　卷積是在媒體處理中非常常用的操作，因而許多處理器都可以在一個周期內完成一條乘累加(MAC)指令，同時還可以完成多個數據的訪問操作(讀或寫)。

圖4 (a)FIR濾波器的公式和結構  (b) IIR濾波器的公式和結構

無限沖擊響應(IIR)濾波器

　　與輸出僅僅取決于輸入的FIR濾波器不同，IIR濾波器則依靠輸入和過去的輸出。IIR濾波器的基本公式是一個差分方程，如圖4b所示。由于當前輸出對于過去輸出的依從關系，IIR濾波器經常被稱為“遞歸式濾波器”。圖4b也給出了IIR濾波器結構的圖示。

快速傅里葉變換

　　我們往往可以更好地描述音頻信號的特性，那就是用頻率組成。傅里葉變換以時域信號作為輸入，并把信號重新安排到頻域里，而傅里葉反變換則完成逆向的工作，把頻域表示變換回時域。從數學上看，時域中的操作與頻域中的操作之間存在一些很妙的特性關系。特別是，時域卷積(或者FIR濾波器)等效于頻域的相乘。如果沒有傅里葉變換這個特別的優化方法，即快速傅里葉變換(FFT)，那么這個信號處理中的珍品就不可能變為實用。事實上，FIR濾波器往往有更高效的實現方法，那就是把輸入信號和濾波器系數用FFT變換到頻域，然后將兩個變換式相乘，最后再用傅里葉反變換把乘積變換回時域。

　　在音頻處理中還經常使用其他一些變換。其中包括最常用的修正離散余弦變換(MDCT)，這是許多音頻壓縮算法的基礎。

采樣率轉換

　　有時您會需要把信號的采樣率轉換到另一個不同的采樣率。用到變采樣率的一個情況是，您需要對一個以8 kHz采樣的音頻信號進行解碼，但是您使用的DAC并不支持這個采樣率。另一個情況是，當一個信號被過采樣之后，需要轉換成一個較低的頻率，因而可以縮短計算時間。把信號從一個采樣率變換到另一個采樣率的過程叫做變采樣率(或SRC)。

　　提高采樣率的方法叫做插值，而降低采樣率的方法叫做抽取。對信號進行M倍抽取是通過只保留每個M樣點而拋棄所有其余的樣點來完成的。對信號進行L倍插值是通過對原來信號的每兩個樣點之間補充L-1個零來完成的。

　　雖然插值和抽取的因子都是整數，但您可以對輸入信號接連使用插值和抽取而得到一個有理數的變換因子。當您用5倍進行上采樣，然后用3倍作下采樣，那么最后的因子為5/3 = 1.67。

圖5  通過上采樣和下采樣的采樣率轉換

　　老實說，我們有點過分地簡化了SRC的過程。為了避免對信號補零(補零會引起頻域的鏡像成分)而引起的人工痕跡，被插值的信號在當作輸出或當作抽取器的輸入而被使用之前，必須經過低通濾波。通過使用一個知曉與L-1個插值樣點相對應的輸入都是零值的特定FIR濾波器結構，這個抗鏡像低通濾波器可以在輸入采樣率下進行，而不必在較快速率的輸出采樣率下進行。

　　同樣，在被抽取之前，不符合Nyquest采樣定律的輸入信號必須被低通濾波，以避免混疊。使用知曉輸出樣點中那些被拋棄的樣點是不需要進行濾波計算的FIR濾波器結構，這個抗混疊低通濾波器可以設計成以抽取后采樣率進行操作，而不必在較快速的輸入采樣率下操作。圖5表示了變采樣率的流程圖。應該注意到，抗鏡像濾波器和抗混疊濾波器是可以合二為一的，以便節省計算量。

　　顯然，對于這些嵌入式音頻的論題，我們僅僅能夠給出一個很表層的討論，但對于嵌入式音頻處理應用的開發，我們還是希望已經提供了一個有用的框架，并提到了其中各種必需考慮的問題。