如今，大多數無線接收器通常都需要有高增益的LNA。作為接收器鏈中的第一個有源組件（active block），LNA應該提供足夠的增益，以克服后續級帶來的噪聲，并盡可能減少噪聲。然而，在一些如IEEE 802.15.4的無線標準中，LNA的噪聲系數（NF）不是一個關鍵的性能參數^1，2。NF要求可以適當放寬，以優化其他設計參數，如增益、功耗和芯片面積。在這篇文章中提出的LNA是專門為IEEE 802.15.4標準設計的。

流行的LNA拓撲結構是源極電感負反饋（inductive source-degeneration）共源LNA（LCSLNA）、共柵LNA（CGLNA）和電阻反饋LNA（RFLNA）。由于其方便的輸入匹配、高增益和低噪聲，L-CSLNA通常是超低功耗窄帶應用的首選^3-6。但是，其增益性能會受到輸入匹配條件的限制。在L-CSLNA的高增益和良好的輸入匹配之間存在一個折衷問題。在這篇文章中，提出的LNA的輸入匹配是通過一個電容反饋方案和一個Л匹配網絡實現的。相比L-CSLNA，電容反饋有助于減少輸入匹配所需的電感數目。此外，利用Л匹配網絡可實現較高的增益和更大的設計自由度。Chung和Shahroury實現了利用電容反饋進行輸入匹配的概念⁷。不過，所使用的LNA采用的是非級聯結構。為了實現高反向隔離，它利用了一個多級結構，這導致了非常高的功耗。提出的LNA采用單級級聯結構，給出了輸入匹配、增益和NF的詳細分析。LNA是采用IBM 0.13μm RF CMOS技術實現的。

源極電感負反饋共源LNA

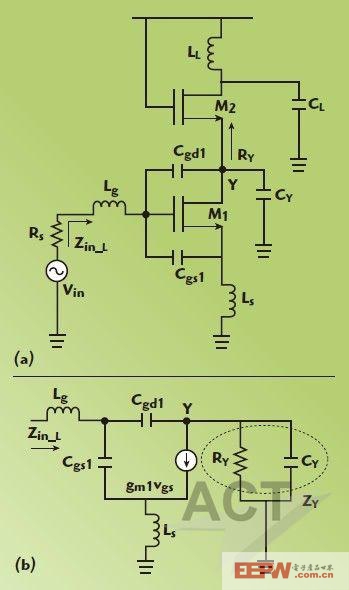
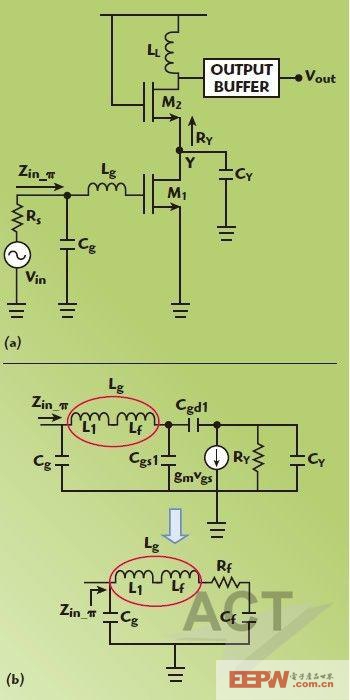
輸入阻抗分析的L-CSLNA原理圖及其等效小信號電路如圖1所示。C_Y包括節點Y的所有寄生電容，可以近似為：

R_Y是來自節點Y的M₂源的總阻抗，在此電路中，R_Y可近似為1/gm2，此處的gm2是晶體管M2的跨導。推導出的L-CSLNA的輸入阻抗是：

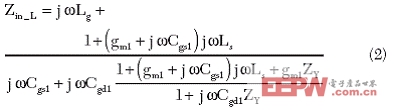
其中是工作頻率，Cgs1和Cgd1是寄生柵源和柵漏電容，gm1是晶體管M1的跨導。當 時，Zin_L可以簡化為：

這與經典結果是一致的。在諧振頻率，輸入阻抗Rin_L等于gm1Ls/Cgs1和晶體管gm1的跨導，可有效地提高Geff_Lgm1，其中Geff_L是：

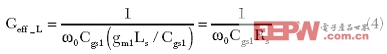
0是諧振頻率。在輸入匹配條件下這個LNA的噪聲系數是：

在方程5中，RLg是電感Lg的寄生串聯電阻，Rg是晶體管M1的柵極電阻， ?和 分別是晶體管M1和M2的漏電流噪聲， 是輸入源電壓噪聲。大gm1和小Cgs1是實現高增益和低噪聲所必需的^4，5。由于輸入匹配條件，Ls的值通常相當小。小Ls的要求有時會成為LNA設計的一個困擾，因為不是所有的電感值都適用于工藝設計套件（PDK）。

提出的具有匹配網絡的電容反饋CSLNA

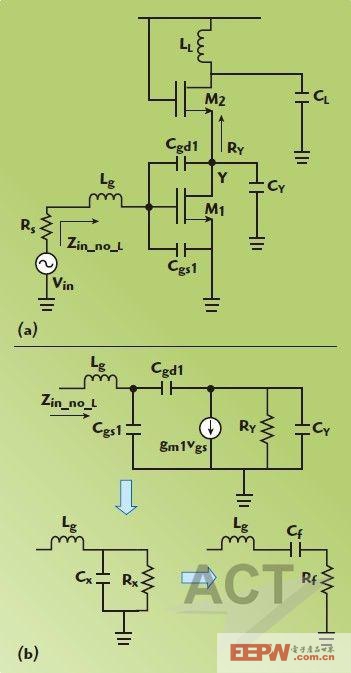
Cheng⁷介紹的LNA使用了輸入器件的寄生柵漏電容和輸出電容CL，以形成電容反饋匹配網絡。只有一個電感用來實現輸入匹配。不過，該分析只適用于非級聯結構。對于CS拓撲結構，要有高反向隔離和良好的穩定性，級聯是首選的結構。在這里，介紹了級聯結構的分析。其原理如圖2所示。基于小信號電路（b），級聯電容反饋LNA的輸入網絡可以轉換為一個包括Lg、Cf和Rf的串聯RLC匹配網絡。Cf和Rf的值可以推導得出：

且

Cx和Rx可以按以下方程計算

為了實現輸入匹配，Rf的設計等于Rs。此輸入匹配網絡的有效增益是：

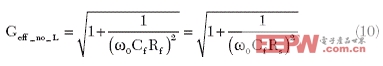
該LNA在輸入條件觀看到的噪聲系數可以推導得出：

與L-CSLNA相比，電容反饋LNA需要的輸入匹配電感數量較少。但這樣做的好處伴隨著較高NF的折衷問題，這可以從方程5和11觀察到。從方程4和10看到，以上討論的兩個LNA的輸入網絡的有效增益受到了50 Ω匹配條件的限制。為了實現良好的輸入匹配，Rf和（gm1Ls/Cgs1）必須匹配到50 Ω。這將限制Geff_L和Geff_no_L的選擇，因此限制了這兩個LNA可實現的增益。在這兩個LNA中存在著高增益和良好的輸入匹配之間折衷的問題。