我們在本系列文章的前一部分[鏈接]已經討論了鎖相環(PLL)的應用以及在時鐘分配系統中，PLL相對于傳統振蕩器的優勢。接下來我們將會闡述基于PLL的時鐘分配系統的重要參數，這些參數都是設計時必須考慮的。例如，在實踐過程中，時鐘的準確時序對所有分配系統而言都非常重要。如果時鐘位置偏差范圍大，則可能會導致系統發生故障。時域中的這些偏差被稱為“抖動”。此外，抖動又分多個類別，譬如周期性抖動、周期間抖動、RMS抖動、長期抖動以及相位抖動。在本章節，我們將重點闡述“相位抖動”，其在頻域中可被稱之為“相位噪聲”。

相位噪聲與相位抖動

　　相位噪聲與相位抖動是時鐘分配系統的關鍵參數，因為時鐘信號的質量在很大程度上取決于其相位噪聲與相位抖動。數字I/O的最大速度受到時鐘時序誤差的限制。隨著技術不斷進步，對時序精確性的要求也越來越高，時鐘必須具有準確的邊緣和高穩定性。

　　理想情況下，時鐘邊緣與其預期位置之間不得存在偏差。但是在實踐過程中，時鐘源極易受到噪聲的影響，進而導致時鐘邊緣偏離于理想位置。這就稱之為抖動。基于PLL的頻率合成器主要用于確保輸出頻率在規定工況下的準確度。其中一條關鍵要求就包括良好的相位噪聲和相位抖動性能，在頻域中，相位噪聲就代表時鐘信號噪聲，而相位抖動是時域的說法，表示時鐘信號不穩定。時間與相位可互換使用，從而對抖動與相位噪聲進行量化。

　　系統中過多的抖動會提高誤碼率，有可能超過系統級要求。射頻和A/D數據轉換應用需要采用相位噪聲非常低的時鐘。對于射頻應用，相位噪聲增加后，可能會產生通道間干擾，進而削弱射頻信號質量。對于ADC應用，如果相位噪聲較高，可能會限制信噪比(SNR)，增加量化誤差。

　　相位噪聲現象是PLL設計人員目前所面臨的一個主要問題。所有現實環境中的振蕩器和信號發生器均存在相位噪聲，但相位噪聲是不受歡迎的，因為它可能會導致傳統接收器中收到的信息失真或完全丟失。因此，必須了解和量化相位噪聲，從而最大限度地降低相位噪聲對較高層次產品的影響。

相位噪聲：

　　了解相位噪聲之前，我們首先來了解一下理想的正弦信號。正弦波是周期性模擬信號的基本形式。正弦信號可以表示為：

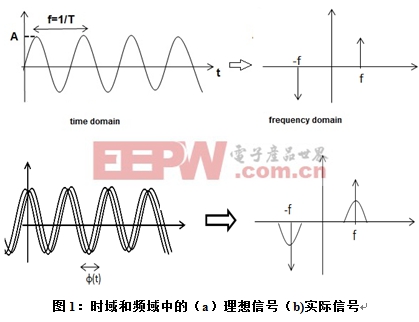
　　如圖1(a)所示，理想的正弦信號是單調波。這意味著，理想的正弦信號只有一個頻率分量，其整個功率均在該分量之中。這一點可以通過傅里葉變換觀察到。然而，環境及/或信號源噪聲會導致信號的振幅和相位出現一定波動。

　　通過傅里葉展開，我們可以看到任何信號均可以分解成多個具有不同頻率和振幅的正弦信號。因此，傅里葉變換將顯示功率譜在多個頻率上分布。圖1(b)從時間和頻率兩個角度分別顯示了正弦信號。如果信號功率分布在一個頻帶上，這意味著該信號攜帶多個不需要的頻率分量。

　　振蕩器的相位噪聲具有短期不穩定性，從頻域角度來描述是最好的，這樣可以通過測量中心頻率任一側的噪聲邊帶來顯示頻譜密度。在實踐中，大多數相位噪聲測量都會出現一條邊帶。如上所述，理想信號會精確按照載波頻率表現出單個脈沖，信號功率全部包含在該脈沖之中。對于實際信號，噪聲會導致功率在范圍較寬的頻帶上分布。

　　相位噪聲的單位一般采用dBc/Hz，1Hz帶寬載波在給定偏移頻率下產生的噪聲功率與載波功率之比即為相位噪聲。dBc是載波分貝的縮寫，用于確定邊帶相位噪聲特性。

　　圖2顯示了非理想振蕩器的典型輸出頻譜。此頻譜顯示了1-Hz帶寬在偏移頻率為f0下的噪聲功率以及fc下的載波功率。

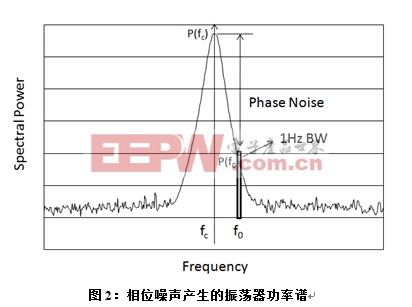
　　雖然圖2引入了雙邊帶這一概念，但在實踐中，大部分相位噪聲的測量都是利用單邊帶完成的。表達公式如下所示：

　　￡(f)=10log{P(f0)/P(fc)}