在數據的加解密領域，算法分為對稱密鑰與非對稱密鑰兩種。對稱密鑰與非對稱密鑰由于各自的特點，所應用的領域是不盡相同的。對稱密鑰加密算法由于其速度快，一般用于整體數據的加密，而非對稱密鑰加密算法的安全性能佳，在數字簽名領域得到廣泛的應用。

TEA算法是由劍橋大學計算機實驗室的David Wheeler和Roger Needham于1994年發明，TEA是Tiny Encryption Algorithm的縮寫，以加密解密速度快，實現簡單著稱。TEA算法每一次可以操作64bit(8byte)，采用128bit(16byte)作為key，算法采用迭代的形式，推薦的迭代輪數是64輪，最少32輪。為解決TEA算法密鑰表攻擊的問題，TEA算法先后經歷了幾次改進，從XTEA到BLOCK TEA，直至最新的XXTEA。XTEA也稱做TEAN，它使用與TEA相同的簡單運算，但四個子密鑰采取不正規的方式進行混合以阻止密鑰表攻擊。Block TEA算法可以對32位的任意整數倍長度的變量塊進行加解密的操作，該算法將XTEA輪循函數依次應用于塊中的每個字，并且將它附加于被應用字的鄰字。XXTEA使用跟Block TEA相似的結構，但在處理塊中每個字時利用了相鄰字，且用擁有兩個輸入量的MX函數代替了XTEA輪循函數。本文所描述的安全機制采用的加密算法就是TEA算法中安全性能最佳的改進版本－XXTEA算法。

XTEA算法的一輪加密過程如圖1所示：

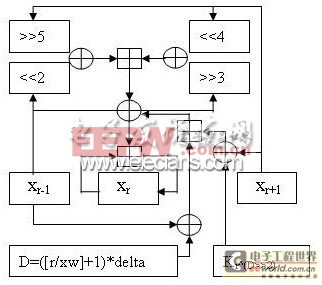
XXTEA算法的結構非常簡單，只需要執行加法、異或和寄存的硬件即可，且軟件實現的代碼非常短小，具有可移植性，非常適合嵌入式系統應用。由于XXTEA算法的以上優點，可以很好地應用于嵌入式RFID系統當中。

XXTEA算法的C語言表達：

#defineMX(z>>5^y2) + (y>>3^z4)^(sum^y) + (k[p3^e]^z);

longbtea(long* v, long n, long* k)

{unsigned long z=v[n-1], y=v[0], sum=0, e, DELTA=0x9e3779b9;long p, q ;

if (n > 1) {/*加密過程*/

q = 6 + 52/n;

while (q-- > 0)

{sum += DELTA;e = (sum >> 2) 3;

for (p=0; pn-1; p++)y = v[p+1],z = v[p] += MX;

y = v[0];z = v[n-1] += MX;}

return 0 ;

} else if (n -1) {/*解密過程*/

n = -n;q = 6 + 52/n;sum = q*DELTA ;

while (sum != 0) { e = (sum >> 2) 3;

for (p=n-1; p>0; p--) z = v[p-1], y = v[p] -= MX;

z = v[n-1];y = v[0] -= MX;sum -= DELTA; }

return 0; }return 1; }

上述算法描述中，v表示為運算的長整型數據的首地址，k為長整型的密鑰的首地址，n表示要要運算的組元個數，正表示加密，負表示解密。N是以32bit為基本單位的組元個數。

訂正：對于加密的示意圖，在Xr-1到>>3那里，是不經歷異或的運算的。